Education Technology
Sign Up for TI Emails

Puzzling Students to Push Their Understanding

Posted 02/25/2022 by Timothy Collier (@tcollier314)

“Mr. Collier, what does it mean to justify my work?” seemed a simple enough question to answer. I quickly replied, “Explain how you got to your answer and why you chose the solution method that you did.” But, unbeknownst to that student, the question sent a chill down my spine. Can my students justify? Will they? Do I know how to help them?

All of these lingering questions came into focus when the teachers in my school began work with Oklahoma Excel, a statewide networked improvement community dedicated to using the principles of improvement science to study that very goal. Can our students increase their mathematical reasoning and justification skills?

In the fall of 2019, the teachers in my department began to think seriously about these questions. Our work began to revolve around a quote shared with us by Doug Roberts, our T³™ in-classroom systemic coach. He said: “My definition of a good teacher has since changed from ‘one who explains things so well that students understand’ to ‘one who gets students to explain things so well that they can be understood.’”*

This mindset shift was what was needed. Along with the other teachers in Oklahoma Excel, we began to test and perfect Puzzle Problems. These are short, five to 15 minute accessible problems that allow students to practice justifying their answers first collaboratively, then individually with problem stems like “Which one does not belong?,” “Always, sometimes or never?,” and “Would you rather?,” we began to learn how to help students learn to justify. Guidance for getting students started can come from any number of sources. I have included a couple of examples.

The Oklahoma Excel teachers provide students with a rubric:

Justification Rubric. Used with permission.


Jennifer Findley, at www.jenniferfindley.com, guides students to justify with an anchor chart:

Justification anchor chart.


We realized early on in teaching justification that student mindsets had to be addressed. Students needed to develop a level of comfort with the idea of justifying their work. To begin to shift those mindsets, we began to look for strategies. Having learned at T³IC of Peter Liljedahl’s, Ph.D., “Building Thinking Classrooms,” we tried his Vertical Non-Permanent Surfaces structure. We sent students to whiteboards in groups of three. They received questions like the following, on their TI-Nspire™ CX family graphing calculators.


While it is not true for all Puzzle Problems, the problems we chose to begin this teaching have no “correct” answer. This gives the teacher the freedom to focus on each group’s presentation. This makes all the difference.

We began to see students debate, stating evidence by using mathematics. Here is a sample of student work from the restaurant problem.

Justification of the restaurant question.


Every group in this class presented their arguments with multiple representations and passion. Finally, we began to see our students move toward this kind of thinking. They started to arrive in our classrooms asking, “Is this a Puzzle Problem day?” We reckoned that we were on to something.

As a department, we continued to branch out. For example, we learned that the Puzzle Problem format could be used to elicit exploration from our students.

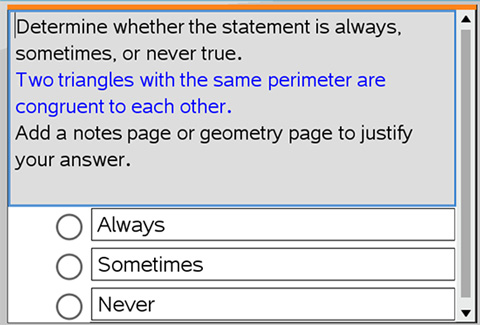
Puzzle Problem by Tracy Matthews, McAlester High School.


Working individually or in small groups, the focus of the problem is the exploration and subsequent justification of the mathematical concept that is the objective of the lesson.

We began to see more connections. Doug Roberts, our T³™ in-classroom systemic coach and our Oklahoma Excel NIC, guided us to think about connecting this work to cognitively challenging tasks. We learned that problems in our textbooks could be transformed into Puzzle Problems. This traditional problem from a typical Pythagorean Theorem practice could be re-written in such a way as to evoke exploration and justification.


It can be rewritten like this:


As we move forward with this work in light of the NAEP 2026 framework, we believe that the next natural step to explore is that of mathematical modeling. We have begun working to understand how the aim of improving student reasoning and justification skills can support real mathematical modeling in our classes in the near future.

If you were intrigued by this blog and wish to learn more about how to design and facilitate engaging problems, check out the on-demand webinar “Puzzle Problems — the Path to Student Justification.”

*Steven C. Reinhart, “Never Say Anything a Kid Can Say,” Mathematics Teaching in the Middle School, Vol. 5, Issue 8 (2000): 478–481.


About the author: After spending 34 years as a secondary math teacher in Oklahoma, Tim Collier now serves as the secondary academic design coordinator for McAlester Public Schools, McAlester Oklahoma. He is a T³™ regional instructor, an Oklahoma Excel improvement fellow, and a finalist for the President’s Award for Excellence in Math and Science Teaching.

Tags:

Tagcloud

Math STEM coding classroom resources TI-84 Plus CE science Python graphing calculator TI-Nspire CX II activity STEM and coding TI Back To School high school calculus TI-84 Plus CE graphing calculator computer science calculator school

Archive

Syndication

© Copyright 1995-2024 Texas Instruments Incorporated. All rights reserved.

TrademarksSoftware Data PolicyPrivacy PolicyCookie PolicyTerms of UseTerms of Sale & ServicesSupply Chain Transparency
About UsNews CenterContact TI