Leveraging CAS To Explore & Teach Mathematics, Part 2
In my previous blog post titled “Leveraging CAS To Explore and Teach Mathematics,” I demonstrated how to utilize CAS in the algebra I classroom. As mentioned in my algebra I post, CAS isn’t only a way to find the answers, CAS can be leveraged to explore and teach concepts in the math classroom. In this follow-up post (part 2), I intend to present ideas for how CAS can be utilized to benefit the algebra II classroom.
Finding a lowest common denominator
In my algebra I post, the Factor tool was employed as an approach to motivate students to recognize patterns between the prime factors of a number and how to use those factors to simplify a radical with the corresponding radicand. In algebra II, the Factor tool can support students in finding the least common denominator for two rational variable expressions. Before showing the capacity of CAS in completing this process in algebra II, I want to first show how this same concept can be numerically explored in middle grades math on the non-CAS TI-Nspire™ CX II graphing calculator. On a Calculator page, use the algebra menu to access the Factor tool, and calculate factor(6) followed by factor(10). On the next line, access the Least Common Multiple tool from the algebra menu and calculate lcm(6, 10).

These calculations support that a least common multiple (or least common denominator) can be determined from the prime factors of the two denominators. In this case, because 2 and 3 are factors of 6, and 2 and 5 are factors of 10, the least common denominator can be determined by multiplying the unique factors that make up each number, 2*3*5 = 30. More examples should be explored for students to confirm the observed pattern.
Now, let’s observe the power of CAS to help build on previously learned math to determine a common denominator for two rational expressions containing variables. (Note: This next process can only be performed on the TI-Nspire™ CX II CAS graphing calculator.) Suppose you want to add the two expressions shown below:
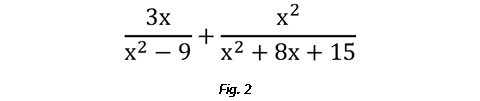
To begin building the common denominator, factor each denominator expression. On a Calculator page, access the Factor tool from the algebra menu, and calculate factor(x2 – 9). On the next line, calculate factor(x2 + 8x + 15).

CAS quickly displays the factors for each expression. On the next line, go to the algebra menu, select Fraction tools, and access the Get Denominator tool. Type in the rational expressions to be added as shown below.

In the same way as using a non-CAS calculator to help enhance the connection between the numeric factors of individual denominators and the lowest common denominator, CAS confirms the same relationship is true for variable expressions. There are not enough cases to establish a pattern, so choose additional examples wisely, and let CAS lead the discussion. (I typically choose a case where one denominator has a “repeated factor” and/or a denominator containing a factor of “x.”)

Transformations of functions
In part 1 of this post, which highlights usage of CAS in algebra I, I used the Solve tool to encourage students to consider the number of solutions to a quadratic equation in the form x2 = a. In algebra II, I have found success using the Solve tool to increase student understanding of transformations of functions. Typically, I have students begin exploring transformations using a TI-Nspire™ file on their handhelds where a parent function can be manipulated using a slider to observe how the function rule, graph and coordinate pairs of a parent function change based on defined parameters. For example, the video below demonstrates a file I use to introduce students to translations of functions.
Though there is nothing CAS-specific in this initial introduction to translations, CAS plays a crucial role in what happens next. Most students leave the initial investigation comprehending that if y = f(x) + k, a function translates “up” k units and if y = f(x + k), a function translates “left” k units. However, many students leave the investigation puzzled as to why in one instance “+ k” results in a positive movement, up, and in the other instance, “+ k” results in a negative movement, left. CAS to the rescue!
For students to gain a clearer understanding of parameters from x’s perspective, the function must be altered to be written in terms of x. On a Calculator page, access the Solve tool in the algebra menu and calculate solve(y=√x, x). (Note: For this demonstration, I typically use the square root function because it’s easier for students to understand the steps involved in solving for “x.”)
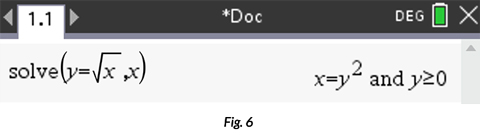
This step is crucial for students to first recognize that the parent function y = √x is x = y2 from “x’s perspective,” the foundation for the comparison to follow. (Note: It’s not a bad idea to spend a little time discussing the “and y ≥0” message that follows.) On the next line calculate solve(y = √(x+3), x).

This single CAS calculation helps to encourage that, from x’s perspective, the parent function x = y2 has changed by “subtracting 3,” and thus, translates the parent function “left” 3 from its original location. More examples can be explored on a Notes page using sliders as seen on problem 1.1 in the video below.
The same parameter confusion also occurs when students observe y = k∙f(x) as a vertical dilation by k but y = f(k∙x) as a horizontal dilation by 1/k. Add another line to the Calculator page and calculate solve(y = √2x,x).

Again, have students explore more examples, as seen on problem 2.1 in the video posted above, to validate the pattern.
Students really struggle when both horizontal parameters are present at the same time. Hopefully, CAS helps students improve perspective in their understanding.

Exploring imaginary numbers
I often utilize CAS to support student learning when new concepts have direct relation to those previously learned. Such is the case when students encounter non-real numbers due to taking the square root of a negative number. On a CAS calculator, you can evaluate square roots of negative numbers if you change the “Real or Complex” settings to “Rectangular.” Once this has been completed, calculate √(-1).

On the next couple of lines, have students calculate √12 and √(-12).

CAS assists students in observing that the process for evaluating radicals does not numerically change for negative radicands, it only creates the presence of i in the simplification. I typically use a Notes page here for students to observe more examples.
Observing patterns in the binomial theorem
Finally, I’d like to present an example of how I use CAS to explore the binomial theorem. I realize this isn’t necessarily standard content in an algebra II curriculum, but I could not teach the binomial theorem as well without CAS. The initial step in understanding the binomial theorem is to first recognize patterns in expanding binomials. Before CAS, I had my students expand (x + y)n “by hand,” usually up to the power of 4. Needless to say, my students made more mistakes in their expansions than they did connections to the forthcoming binomial theorem. With the power of CAS in my students’ hands, they are empowered with the ability to efficiently expand binomial expressions so that more time can be spent making valuable connections to observed patterns. On a Calculator page, access the Expand tool from the algebra menu and calculate expand((x + y)2, x).
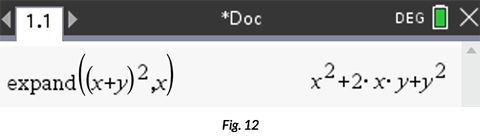
Continue this process for higher expansion powers, or better yet, set up a Notes page where students can use a slider to swiftly observe multiple expansions of (x+ y)n.
I typically have students write down expansions through the fourth power and then challenge them to use the initial expansions to write out (x + y)5. Students often struggle with the coefficient part of the expansion, so one thing that can be helpful is to have students use a tool that extracts the coefficients in the expansion. To do this (I had to dig deep into the menus to find this tool), go to the algebra menu, select Calculations, Algebra, Polynomial tools, and then Coefficients of Polynomial. Calculate polyCoeffs(expand(x+1)n, x). (Notice I have replaced y with 1 so that y is not part of the coefficients determined.)

Add this to a Notes page (as seen in the video below), and now you have a dynamic document that expands (x + y)n and displays its coefficients simultaneously. Click on the slider and you will observe Pascal’s triangle come to life. Now, let the pattern exploring begin. These last calculations have also been helpful in applying the binomial theorem to finding binomial probabilities in a later lesson.
I hope these examples offer a glimpse into the power and potential utility of CAS in the algebra II classroom. CAS continues to be my own personal playground for finding new ways to effectively teach math to my students. Remember, CAS isn’t only on the handheld to find answers, it’s an important tool to help understand them as well.
About the author: Scott Knapp has been teaching math for 21 years and has served as a T³™ Regional Instructor for 10 years. He currently teaches at Glenbrook North High School in Northbrook, Illinois, a northern suburb of Chicago. Knapp is an advocate for using TI technology and regularly presents at conferences, workshops and webinars, demonstrating how TI technology can be effectively used by students to explore and learn mathematics. Follow Knapp on Twitter @scottknapp.
Tags:
Tagcloud
Archive
- 2025
- 2024
- 2023
- 2022
-
2021
- January (2)
- February (3)
- March (5)
-
April (7)
- Top Tips for Tackling the SAT® with the TI-84 Plus CE
- Monday Night Calculus With Steve Kokoska and Tom Dick
- Which TI Calculator for the SAT® and Why?
- Top Tips From a Math Teacher for Taking the Online AP® Exam
- Celebrate National Robotics Week With Supervised Teardowns
- How To Use the TI-84 Plus Family of Graphing Calculators To Succeed on the ACT®
- AP® Statistics: 6 Math Functions You Must Know for the TI-84 Plus
- May (1)
- June (3)
- July (2)
- August (5)
- September (2)
-
October (4)
- Transformation Graphing — the Families of Functions Modular Video Series to the Rescue!
- Top 3 Halloween-Themed Classroom Activities
- In Honor of National Chemistry Week, 5 “Organic” Ways to Incorporate TI Technology Into Chemistry Class
- 5 Spook-tacular Ways to Bring the Halloween “Spirits” Into Your Classroom
- November (4)
- December (1)
-
2020
- January (2)
- February (1)
- March (3)
- April (1)
- May (2)
- July (1)
- August (2)
- September (3)
-
October (7)
- Tips for Teachers in the time of COVID-19
- Top 10 Features of TI-84 Plus for Taking the ACT®
- TI Codes Contest Winners Revealed
- Best of Chemistry Activities for the Fall Semester
- Best of Biology Activities for the Fall Semester
- Best of Physics Activities for the Fall Semester
- Best of Middle Grades Science Activities
- November (1)
- December (2)
- 2019
-
2018
- January (1)
- February (5)
- March (4)
- April (5)
- May (4)
- June (4)
- July (4)
- August (4)
- September (5)
-
October (9)
- Art in Chemistry
- Which Texas Instruments (TI) Calculator for the ACT® and Why?
- Meet TI Teacher of the Month: Jessica Kohout
- Innovation in Biology
- Learning With Your Students
- A first-of-its-kind STEM strategy charts path to help educators
- #NCTMregionals Hartford 2018 Recap
- The Math Behind “Going Viral”
- Real-World Applications of Chemistry
-
November (8)
- Testing Tips: Using Calculators on Class Assessments
- Girls in STEM: A Personal Perspective
- 5 Teachers You Should Be Following on Instagram Right Now
- Meet TI Teacher of the Month: Katie England
- End-of-Marking Period Feedback Is a Two-Way Street
- #NCTMregionals Kansas City 2018 Recap
- Slope: It Shouldn’t Just Be a Formula
- Hit a high note exploring the math behind music
- December (5)
- 2017
- 2016
- 2015
