Test your math strength against former pro-football player, John Urschel
Do you have what it takes to go head-to-head with former pro-football player turned professional mathematician, John Urschel? Now is your chance to flex your mental muscles and find out.
Each problem tackles a subject from chess to cryptography -- things students are naturally interested in – and force students to explore the math behind them. John, who is currently pursuing his PhD in math at MIT, created each of the questions himself and wants to see students exercise their brains as they kick-off a new school year. John’s first problem looks for mathematics in one of his all-time favorite hobbies, chess. Let’s start the game clock!
John Urschel, MIT mathematics PhD student and former NFL player
Problem 1 | Chess
On a chessboard, it takes a king, on the h4 square, six moves to reach the b4 square. How many different, six move routes could the king take?
Problem 2 | Virality
Suppose we have the following model for information (e.g. photo, video, post) transfer (i.e. spread) in a grid: each square is colored either green (if it knows a given piece of information) or red (if it does not). A red square learns this information (becomes green) if at least two of its neighbors (sharing an edge) already knows it. For example, in this situation the bottom middle square becomes green:
On a 10 X 10 grid, what is the minimum number of initial green squares needed for the entire grid to become green?
Problem 3 | Cryptography
Here’s a Valentine’s Day cryptoarithmetic puzzle. Is it possible to replace each unique letter in this equation with a unique digit (0 to 9) so that it holds? Note that once a letter is given a digit, that is its digit throughout the equation (if you set O to be 3 in YOU, it is also 3 in LOVE).
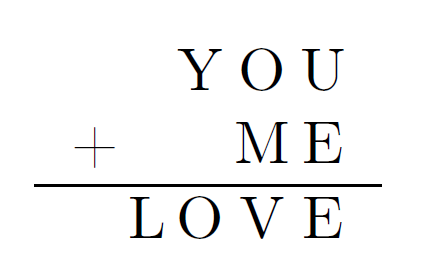
Problem 4 | Music
There are 88 keys on a piano, with the lowest note being A0, with a frequency of 27.5 Hertz. Two consecutive keys differ in frequency by a factor of 12√2. The note A1 is the lowest piano note with an integer frequency (55 Hz). Does there exist a piano note with integer frequency other than octave shifts of A1?
Problem 5 | Football
Your team is down 14 points with three minutes to go in the 4th quarter and score a touchdown. Should they go for one or two? (Assume your kicker makes extra points 100% of the time and your team has a 50% chance of winning in overtime)
Problem 6 | The Lottery
There is a lottery where five balls are sequentially drawn (without replacement) from a bin of fifty balls containing five copies of the numbers 0 through 9. If you guess all five numbers correctly, your prize is the product of the multiplicities of the numbers drawn (for example, 1, 2, 1, 1, 2 gives a prize of six). What lottery ticket would you buy?
Solutions
Problem 1 Solution:
The number of six move routes is actually equivalent to the number of strings consisting of -1, 0, +1 of length six that add up to zero (the path h4-g3-f3-e2-d3-c4-b4 would correspond to -1, 0,-1,+1, +1, 0):
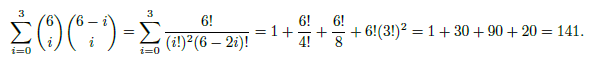
What if you had the setup below? What move would you play as white?
The chess puzzle is a famous one, composed by Grigoriev. An attack on the b7 pawn loses:
1. Kg5 Kc2 2. Kf4 Kd3 3. Ke5 Kc4 4. Kd6 Kb5 5. Kc7 Ka 6.
Of the 141 routes the white king has to get to b4, only one holds the draw:
1. Kg3! Kc2 2. Kf2! Kd3 3. Ke1! Kc4 4. Kd2 Kb5 5. Kc3 Kxb6 6. Kb4.
Problem 2 Solution:
Making either long diagonal exclusively green (10 initial green squares) is enough to make the entire grid green (after k steps, all squares within distance k of the diagonal becomes green). The hard part is showing that you need at least 10 squares. One way to do this is by using something called a “monotonicity" argument. Note that the total perimeter of the green squares never increases, but is 40 if the entire grid is filled.
Problem 3 Solution:
Sadly, we just can’t make this equation work. Because U + E has E in the ones place, we know U is zero. Y, L and O have to be nine, one, and zero, otherwise we can’t get a four digit number from a three and two digit one. But the problem is that O+M has to be at least eleven, which isn’t possible if O is zero. This equation just isn’t meant to be.
However, it turns out that just by adding in math, we can make this equation work, and be indivisible (YOU, ME, MATH, and LOVE are all prime numbers). This one is not for the faint of heart, but if you enjoyed this challenge, you might want to give this one a try. The solution is unique.
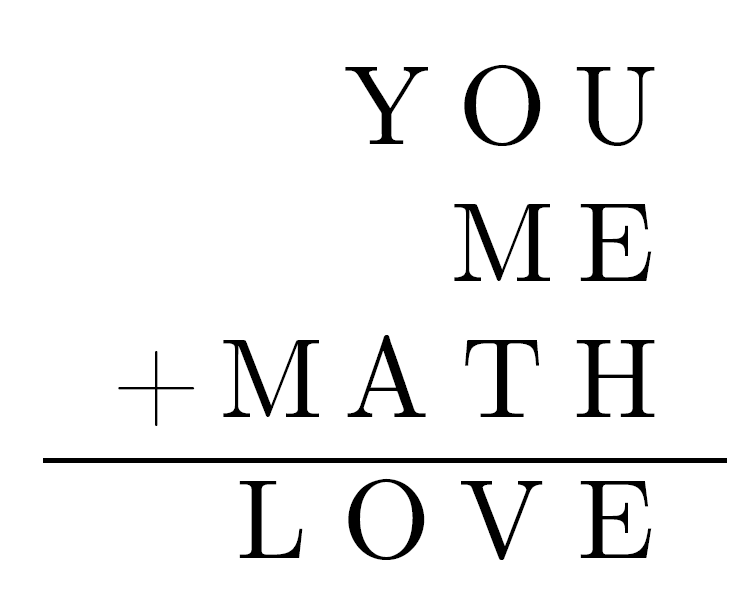
Problem 4 Solution:
Because A1 is the lowest piano note with an integer frequency, it suffices to consider only notes higher than A1. If a note is k keys higher than A1, then its frequency is given by 55 X 2k/12. If the note is not an A note, then k can not be a multiple of 12. The question is if there exists a k which is not a multiple of 12 such that 55 X 2k/12 is an integer. It suffices to show that 2k/12 is irrational for all k not a multiple of 12.
We will prove something even stronger, that any fractional power of a prime is irrational. We will prove this by contradiction. Let p be a prime and x a positive fraction. x is not a whole number, and so can be written as x = a/b where a and b (b ≠ 1) are relatively prime natural numbers. Suppose px is rational. Then px =pa/b = q for some rational number q. Then pa = qb, and q must be a power of p, q = pc (because p is prime). But this implies that a = bc, which contradicts the assumption that a and b are mutually prime.
Therefore, all piano notes with integer frequency must be an A note in some octave.
Problem 5 Solution:
This is a famous example of decision making in football (and a fun application of the quadratic formula). The key is that because there is so little time left, if the opponent scores, the game is over. If you decide to kick the extra point, and score again, you will again kick the extra point (suppose two point conversion rate is under 50%, otherwise why are we having this conversation?) and then have a 50% chance of winning in overtime.
Suppose your team succeeds in a two point conversion 100 X p% of the time. If they succeed, then on the next touchdown, they can simply kick the extra point and win. But there is a 100 X (1 - p)% chance that they will fail, and have to go for two on the next touchdown, just to make it to overtime. So there is a 100 X [p + .5(1 - p)p]% of winning, given your team gets a second touchdown
When should you go for two? When your chance of winning is at least as good by doing so, namely, when
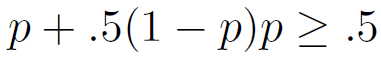
Using the quadratic formula, this occurs when
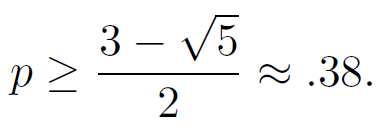
Problem 6 Solution:
This is certainly a mathematician’s lottery, as you have to weigh both the prize and the likelihood of your sequence occurring. Let’s consider the expected prize in each case:
- no repeats: 5⁄50 × 5⁄49 × 5⁄48 × 5⁄47 × 5⁄46 chance of winning, 1 unit prize
- one repeats: 5⁄50 × 4⁄49 × 5⁄48 × 5⁄47 × 5⁄46 chance of winning, 2 unit prize
- two repeats: 5⁄50 × 4⁄49 × 5⁄48 × 4⁄47 × 5⁄46 chance of winning, 4 unit prize
- one triple: 5⁄50 × 4⁄49 × 3⁄48 × 5⁄47 × 5⁄46 chance of winning, 3 unit prize
- one triple, one repeat: 5⁄50 × 4⁄49 × 3⁄48 × 5⁄47 × 4⁄46 chance of winning, 6 unit prize
- one quadruple: 5⁄50 × 4⁄49 × 3⁄48 × 2⁄47 × 5⁄46 chance of winning, 4 unit prize
- one quintuple: 5⁄50 × 4⁄49 × 3⁄48 × 2⁄47 × 1⁄46 chance of winning, 5 unit prize
It turns out that even though a ticket with five distinct numbers is more likely to win, when you take prizes into account you should choose a ticket with one triple and one double (I’d choose 6; 4; 6; 4; 6).😉
