Top Tips for Tackling the SAT® with the TI-84 Plus CE
On the SAT® exam, calculators are allowed on one of the two math sections. Read on for tips to leverage your TI-84 Plus CE for success on test day! The example questions explained below are like questions you might see on the SAT® exam.
1. Know Your Tools
Bring a calculator that you are familiar with to the SAT® exam and use it as you prepare with practice questions. There are many TI calculator models allowed on the test; see the SAT® Calculator Policy webpage for the full list. The tips in this post focus on the TI-84 Plus CE model, but they are applicable to the entire TI-84 graphing calculator family.
Be sure your calculator is fully charged or has fresh batteries for test day. And keep in mind that the calculator is not needed for every question; it is sometimes better not to use a calculator because it will slow you down.
2. Know the Test
The Math-Calculator section of the SAT® exam is 55 minutes long and contains 38 questions. There are 30 multiple-choice questions, each with four answer choices, and 8 “grid-in” questions with no choices provided. There is also a set of reference formulas and diagrams provided for your use; so don’t memorize what is already given. For more information about the structure and content of the test , go to the SAT® Math Test webpage.
For the grid-in questions, answers will be 1, 2, 3, or 4 digits long, including any decimal point or fraction bar, and the answer won’t be negative. So if your answer does not meet these guidelines, you know it must be wrong and you will have to try again.
Use the TI-84 Plus CE to help you work more efficiently, compute more accurately, and verify answers. Just like you would in your math class, do some scratch work on the test paper before using the calculator. This enables you to decide if it is a good time to use the tool or not—you should avoid typing easy math operations that you can do mentally. Also, pay attention to the structure of the question (and what it is asking for) because that may save time getting to the correct answer.
3. Use the Home Screen History
When calculating on the home screen, use the previous answer and previous entry history to save some keystrokes and time. Pressing the next operation key immediately after a result will insert Ans so the previous answer is used in the next step and you don’t have to retype numbers.
Example 1:If 26 + 3x is 11 less than 79, find x.
Write the equation: 26 + 3x = 79 – 11 and solve using these algebraic steps:

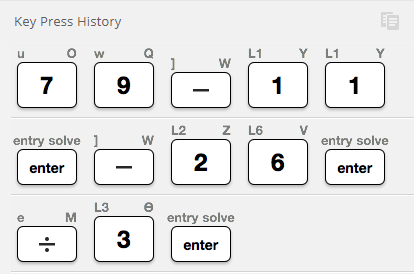
You can also copy and edit previous entries. In example 2, you have an inequality and numerical choices, so you can substitute in one value into the expression to check if it works. Then arrow up twice to highlight the expression and press enter to use it again. Left arrow to edit the value and check the next choice. Stop as soon as you find the right answer.
Example 2:For which value of m will this inequality be true? 17 + 5.5m > –71
A. –88
B. –17
C. –16
D. –5.5
4. Use MathPrint Templates
When questions involve fractions, absolute values, or radicals, use the MathPrint templates built into the TI-84 Plus CE. Access the fraction bar by pressing the alpha key then the X,T,Θ,n key on CE models and alpha then y= on other TI-84 Plus models. You can also easily convert between fractions and decimals. Absolute value and radical templates are found by pressing alpha then window.
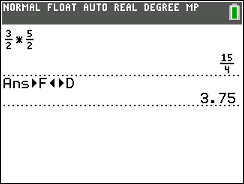
In example 3, multiplying both sides by the reciprocal of 2/5 will solve the problem in one step (instead of taking two steps: multiplying by 5 and dividing by 2). Use the fraction template and convert to a decimal if desired, since both answers will fit in the grid.
Example 3: (grid-in)Solve for x
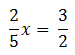
5. Use a Graph
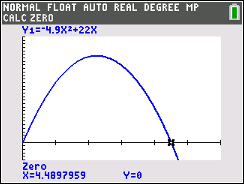
You probably know from your school math class that there is more than one way to solve equations: two methods are to use algebraic operations or to examine a graph. In example 4, you can find how many seconds it takes for a ball to hit the ground by graphing the quadratic equation on an appropriate window and using the CALC menu (press 2nd trace) to find the zero.
Example 4:The equation H = –4.9X2 +22X represents the height H of a ball in meters at time X seconds after it is tossed upward with an initial velocity of 22 meters per second. Approximately when does the ball hit the ground?
A. after 4.0 seconds
B. after 4.5 seconds
C. after 5.0 seconds
D. after 5.5 seconds
6. Substitute Numbers for Math Relationships
One of the trickiest types of SAT® exam questions is when a mathematical relationship is described between two or more variables and you are asked to pick which choice properly represents the relationship. One strategy is to pick some values for the variables, avoiding 0, 1 and numbers that are multiples of each other, like 3 and 6. Then use your calculator to solve the problem numerically with these values. Finally, substitute the values into each given equation to find the one that works.
Example 5:The cost of using a computer at a business center is $0.45 per minute. Which equation represents the cost C in dollars for using the computer for H hours?
A. C = 0.45(60H)
B. C = 0.45H + 60
C. C = (0.45H)/60
D. C = 60H/(0.45H)
Choose a value for H such as 2 hours, and find the cost, which would be $54. Substitute into each answer choice.

When choosing values, don’t forget about negative numbers! In example 6, pick two values for X and Y then test each option, eliminating those that don’t work. After trying a set of positive numbers, option III is eliminated (and so is choice C). Then try X = –5 and Y = –3 in order to finalize the answer.
Example 6:Let X and Y be numbers such that X < Y. Which of the following must be true?
I. X2 < Y2 II. X – Y < 0 III. Y – X < 0
A. I only
B. II only
C. III only
D. I and II only

Need More Help?
Check out these test prep exam resources and product tutorial videos for additional tips.
Best of luck!
About The Author: Karen Campe is a T3™ National Instructor with 15 years’ experience teaching secondary math and pre-service teachers. She is passionate about using all types of technology to enhance student understanding in mathematics and has provided technology professional development at conferences, workshops and webinars since 1998. Karen blogs at karendcampe.wordpress.com. Follow her on Twitter @KarenCampe.
Tagcloud
Archive
- 2026
- 2025
- 2024
- 2023
- 2022
-
2021
- January (1)
- February (3)
- March (5)
-
April (7)
- Top Tips for Tackling the SAT® with the TI-84 Plus CE
- Monday Night Calculus With Steve Kokoska and Tom Dick
- Which TI Calculator for the SAT® and Why?
- Top Tips From a Math Teacher for Taking the Online AP® Exam
- Celebrate National Robotics Week With Supervised Teardowns
- How To Use the TI-84 Plus Family of Graphing Calculators To Succeed on the ACT®
- AP® Statistics: 6 Math Functions You Must Know for the TI-84 Plus
- May (1)
- June (3)
- July (2)
- August (5)
- September (2)
-
October (4)
- Transformation Graphing — the Families of Functions Modular Video Series to the Rescue!
- Top 3 Halloween-Themed Classroom Activities
- In Honor of National Chemistry Week, 5 “Organic” Ways to Incorporate TI Technology Into Chemistry Class
- 5 Spook-tacular Ways to Bring the Halloween “Spirits” Into Your Classroom
- November (4)
- December (1)
- 2020
- 2019
-
2018
- January (1)
- February (5)
- March (4)
- April (5)
- May (4)
- June (4)
- July (4)
- August (4)
- September (5)
- October (8)
-
November (8)
- Testing Tips: Using Calculators on Class Assessments
- Girls in STEM: A Personal Perspective
- 5 Teachers You Should Be Following on Instagram Right Now
- Meet TI Teacher of the Month: Katie England
- End-of-Marking Period Feedback Is a Two-Way Street
- #NCTMregionals Kansas City 2018 Recap
- Slope: It Shouldn’t Just Be a Formula
- Hit a high note exploring the math behind music
- December (5)
- 2017
- 2016
- 2015
