The Math Behind “Going Viral”
As we continue to explore everyday items and concepts that are made with math, this week we are exploring the concept of going viral. I’m sure you remember the star-studded selfie from the 2014 Academy Awards in which an Ellen Degeneres tweet nearly broke the Internet. Within hours it became one of the most-retweeted posts in Twitter’s history, garnering more than 3.3 million retweets.
Which brings me to the question, what exactly does it mean to “go viral? By definition, it means that, on average, every time one person engages with your tweet, they share it and compel at least one other person to share it to their followers as well. This is exponential growth at its finest. We have a quick video that helps explain the concept to your students:
Now, let’s imagine for a moment that you find this blog post and video so compelling (we’re pretending here) that you tweet the link to your followers. You are known as the first generation to check out this blog post on our website. Later in the day, three teachers who were looking for lessons on exponential growth on Twitter see your post, like it and share the link with their followers. Those three teachers are the second generation. From their shares, 50 other people visit our website (third generation). By Wednesday, we’re on our 27th generation, and 10,000 people have visited our website, and my boss is begging me to write more stories on exponential growth!
In all seriousness, what’s important about this example? Each generation contained more people than the generation before. That means that instead of reaching fewer and fewer people as time passed, our video reaches more and more students as time goes on. Below are a few additional examples of exponential growth activities you can try with your students as we continue to connect math to every day concepts.
Exponential Growth: In this algebra II activity, students explore the exponential function y=b^x for different values of b. Students then use a line tangent to the curve at a point to explore the relationship between the slope of the tangent line at that point and the value of the function at the same point. At the end of this activity, students will discover that there is exactly one value of b, Euler’s number, for which the slope of the tangent and value of the function are equal.

Spreading Doom: In this activity, students are introduced to the geometric sequence that models the spread of a virus. Students will relate the growth model to an exponential curve.
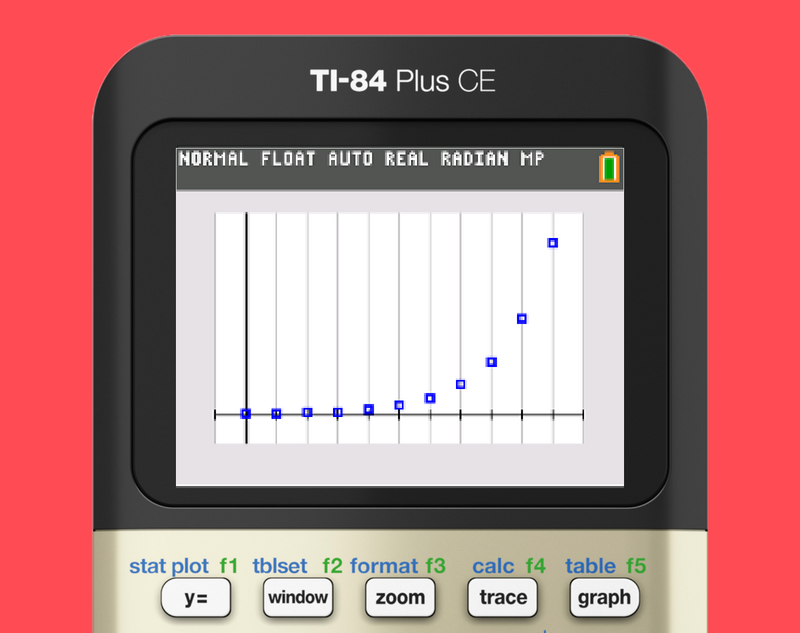
Coin Toss: Students will run two experiments that simulate pouring out coins from a bag. Students will collect data and model the data with different methods for determining the exponential equations.
Tagcloud
Archive
- 2025
- 2024
- 2023
- 2022
-
2021
- January (2)
- February (3)
- March (5)
-
April (7)
- Top Tips for Tackling the SAT® with the TI-84 Plus CE
- Monday Night Calculus With Steve Kokoska and Tom Dick
- Which TI Calculator for the SAT® and Why?
- Top Tips From a Math Teacher for Taking the Online AP® Exam
- Celebrate National Robotics Week With Supervised Teardowns
- How To Use the TI-84 Plus Family of Graphing Calculators To Succeed on the ACT®
- AP® Statistics: 6 Math Functions You Must Know for the TI-84 Plus
- May (1)
- June (3)
- July (2)
- August (5)
- September (2)
-
October (4)
- Transformation Graphing — the Families of Functions Modular Video Series to the Rescue!
- Top 3 Halloween-Themed Classroom Activities
- In Honor of National Chemistry Week, 5 “Organic” Ways to Incorporate TI Technology Into Chemistry Class
- 5 Spook-tacular Ways to Bring the Halloween “Spirits” Into Your Classroom
- November (4)
- December (1)
-
2020
- January (2)
- February (1)
- March (3)
- April (1)
- May (2)
- July (1)
- August (2)
- September (3)
-
October (7)
- Tips for Teachers in the time of COVID-19
- Top 10 Features of TI-84 Plus for Taking the ACT®
- TI Codes Contest Winners Revealed
- Best of Chemistry Activities for the Fall Semester
- Best of Biology Activities for the Fall Semester
- Best of Physics Activities for the Fall Semester
- Best of Middle Grades Science Activities
- November (1)
- December (2)
- 2019
-
2018
- January (1)
- February (5)
- March (4)
- April (5)
- May (4)
- June (4)
- July (4)
- August (4)
- September (5)
-
October (9)
- Art in Chemistry
- Which Texas Instruments (TI) Calculator for the ACT® and Why?
- Meet TI Teacher of the Month: Jessica Kohout
- Innovation in Biology
- Learning With Your Students
- A first-of-its-kind STEM strategy charts path to help educators
- #NCTMregionals Hartford 2018 Recap
- The Math Behind “Going Viral”
- Real-World Applications of Chemistry
-
November (8)
- Testing Tips: Using Calculators on Class Assessments
- Girls in STEM: A Personal Perspective
- 5 Teachers You Should Be Following on Instagram Right Now
- Meet TI Teacher of the Month: Katie England
- End-of-Marking Period Feedback Is a Two-Way Street
- #NCTMregionals Kansas City 2018 Recap
- Slope: It Shouldn’t Just Be a Formula
- Hit a high note exploring the math behind music
- December (5)
- 2017
- 2016
- 2015

