Education Technology
Sign Up for TI Emails

Transformation Graphing — the Families of Functions Modular Video Series to the Rescue!

Posted 10/29/2021 by Tom Reardon

Are your students struggling with graphing the parent functions or how to graph transformations of them? Texas Instruments is here to help teachers — and students — with a video resource that contains over 250 short colorful animated videos with over 460 examples that illustrate and explain these essential graphs and their transformations. This easy-to-use resource can be utilized in several ways:

  • As a teaching and learning tool inside and outside the classroom
  • As independent study and review
  • To augment a flipped classroom


It is modular — you only use what you want or need! And students can work at their own pace.

Explore linear relations and slope
For introducing graphs of linear relationships, here is a screenshot from the video “How to Graph y = mx +b” that has students discover the relationship between the slope, y-intercept and the equation of a line and how to graph the line.

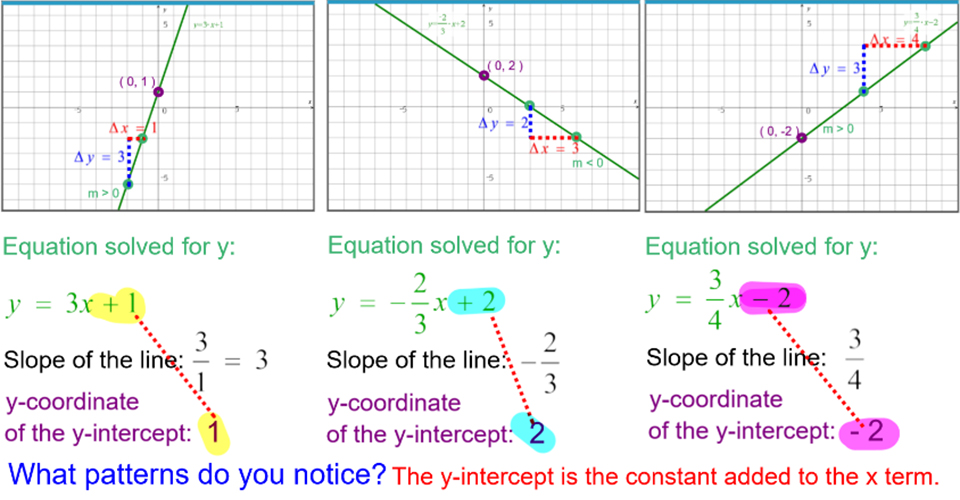
Students should recognize that the y-intercept is always the constant being added (or subtracted) to the term that contains x when solved for y. Also, notice how color is used as a teaching tool to assist students in recognizing patterns, spanning pre-algebra through calculus.

Share this video series with your students to help them learn and discover slope with six short videos on topics as seen in this screenshot from the website.

Check out the first video in this series, “What Slope Means, and Four ‘Flavors’ of Slope.”

Review 15 parent functions and their transformations
There are also modules for 14 common parent functions as well as a module focused on applying transformations to a generic piecewise function included in this video resource. Here is a list of the parent functions that are explained in great detail and also as a quick review.

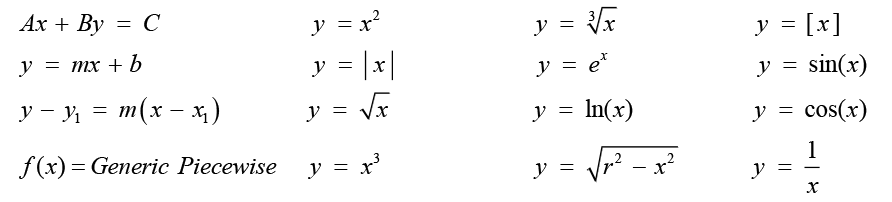
In each function module, you will see the various transformations and combinations of the following transformations illustrated and explained in depth.

For each parent function, the videos give specific examples of graphing the transformed function using every type of transformation, and several combinations of these transformations are also included. Below is an animated GIF of screenshots from the video “Quick! Graph f(x+4)” for a generic piecewise function. Students are encouraged to plot transformations by discovering the patterns and making correct generalizations. Again, notice the use of color to assist this discovery.

One of the most difficult concepts for students to understand is how to graph functions affected by horizontal stretches and shrinks. Here is an animated GIF from the video “Exploring Function Transformations: ” that illustrates how the parameter for the coefficient of x affects the shape of the graph.

In every video, intentional use of proper mathematical terminology is present. For example, the screenshot below shows the terminology for analyzing a sinusoidal function after a combination of transformations has been applied: period, phase shift, point of inflection, maximum, minimum. This is encouraged throughout the video series.

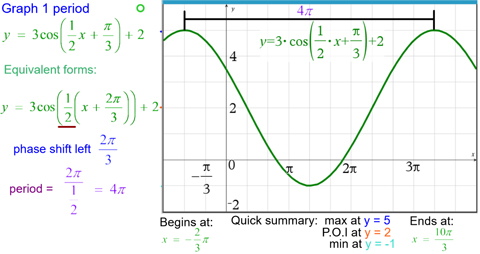
Get started: Download the Quick Reference Guide
In order to access all the content, visit the Families of Functions modular course website, download the Quick Reference Guide and share it with your students. This guide is essential for getting the most out of this video resource. It contains direct links to the YouTube videos for every function and transformation organized by parent function, saving you and your students time. This is very effective in planning investigations as it also includes a listing of each equation that is covered in the video.

This is a partial screenshot for the squaring function video listings.

The guide lists the examples illustrated in the videos, along with “Now you try” examples. There are two links for each video: One is the YouTube link, the other is easier to use and assign. Teachers can ask their students, “Which of these examples are you not able to do?” Then use that video!

Instead of using valuable in-class time, teachers can assign these videos to be done outside of class. This is more efficient for the students. The students who require more assistance can obtain it easily and repeatedly, if they need it. At the same time, those students who just need a quick review are not bored by watching topics they already know and understand. All students can learn at their own individual pace.

About the author: Tom Reardon taught every math course at Fitch High School (Ohio) during his 35-year career, where he received the Presidential Award and attained National Board Certification. He was an adjunct mathematics and computer science instructor at Youngstown State University for 38 years. Since 2009, Reardon has been a senior math advisor for Texas Instruments in product strategy and development. Recently he has been focusing on ACT® and SAT® test prep and the Families of Functions video series.


SAT® is a trademark registered by the College Board. ACT® is a registered trademark of ACT, Inc. Neither are affiliated with, nor endorse, TI products. Policies subject to change. Visit www.collegeboard.org and www.act.org.

Tags:

Tagcloud

Math STEM coding classroom resources TI-84 Plus CE science Python graphing calculator TI-Nspire CX II activity STEM and coding TI Back To School high school calculus TI-84 Plus CE graphing calculator computer science calculator school

Archive

Syndication

© Copyright 1995-2024 Texas Instruments Incorporated. All rights reserved.

TrademarksSoftware Data PolicyPrivacy PolicyCookie PolicyTerms of UseTerms of Sale & ServicesSupply Chain Transparency
About UsNews CenterContact TI