How to introduce your students to computational thinking in the math classroom
In this post, we will go through a few introductory steps to help you get started writing simple TI-Basic programs on your TI-Nspire CX handheld. We will use a familiar mathematical procedure – computing the slope of a line between two points – to demonstrate computational thinking and a few coding concepts. Expressing a problem and a solution in a way that a computer, or human, can carry it out is computational thinking. Coding on the calculator is one method to give students an opportunity to solidify their understanding of a concept and explore computational thinking. It has a similar effect of asking a student to explain something to one of their peers to make sure they understand it. Coding also gives students valuable exposure to writing programs, which can be a powerful experience.
STEP 1: Never programmed? Have them at Hello!
If you’ve never programmed with your calculators, start by displaying “HELLO WORLD” on the screen. This is a common starting point in learning any programming language. Luckily, TI offers step-by-step guidance on how to display text to the screen and other introductory programs in our 10 Minutes of Code resources. Start with Unit 1: Program Basics. The first skill builder will lead you and your students through writing code to display to the screen. These are free lessons you can display from the web or print to share with your students.
STEP 2: Identify what you want to program
You’ve had a chance to write your first program and become familiar with how the commands work within TI-Basic. Now it’s time to identity a math process you want to automate. In this post, we’re going to write a program that calculates the slope of a line between two points.
STEP 3: Break it down into plain English
Using pseudocode is a good way to introduce students to the logic of a program without having to know the coding language. Pseudocode, while it sounds complex, simply means writing in plain English explicitly what you want the program to do. So let’s start with some pseudocode for determining the slope between two points. What is the first thing you need to compute the slope of a line? To make the calculation, you will need the coordinates for two points. Next, you will need to calculate the slope by inserting the coordinates into the slope formula. Lastly, you will need to display the slope. Don’t forget this last, important step. The code runs exactly what you tell it to do, so if you don’t remember to include “display” it won’t know to display the answer.
Below is an example of pseudocode for this logic:
Get two points → calculate slope → display slope
STEP 4: Translate your words to code
Now that we have the pseudocode, let’s translate that to TI-Basic code. The first step in our pseudocode is to get two points. You can do that with the lines of code below. This will prompt the user to input the x- and y-coordinates for the two points and store them in variables with corresponding names.
Now that we have the pseudocode, let’s translate that to TI-Basic code. The first step in our pseudocode is to get two points. You can do that with the lines of code below. This will prompt the user to input the x- and y-coordinates for the two points and store them in variables with corresponding names.
Request “X1?”,x1
Request “Y1?”,y1
Request “X2?”,x2
Request “Y2?”,y2
Next, the program will need to perform the calculation. It is easiest to define a variable called slope. Then, perform the calculation.
slope:=(y2-y1)/(x2-x1)
Finally, just as stated in the pseudocode, you need to display the result. To do this, use the “Disp” command.
Disp slope
Below is a screenshot that shows the entire program. I named it m.
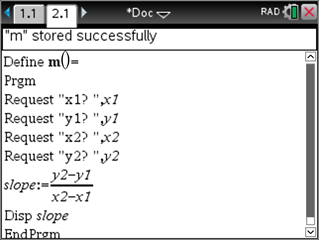
STEP 5: Running and testing your code
One of the really great things about students writing code for a familiar process or procedure is that they must think about the procedure from a big picture perspective. For instance, the above program will work great, so long as x1 and x2 are not equal. But what about dividing by zero? We need a way to deal with the situation of undefined slope. Once your students explore a little bit, they will see a need for dealing with this scenario. Now, your pseudocode will need one extra step.
Get two points → If x1=x2 then → Disp “undefined” → Else → calculate slope → display slope
When students see this logic, it brings home the fact that they don’t need to compute the slope if they recognize that both the x-coordinates are equal. In order to use the if, then, else logic, we need to introduce a new statement. Edit your program and after the Request commands, insert a new line. Starting there, type:
If x1=x2 then
Disp “undefined”
Else
slope:=(y2-y1)/(x2-x1)
Disp slope
EndIf
Note that the if, then, else logic requires an EndIf to close the logic statement. Now, your program will display undefined when the user uses two equivalent x-coordinates. Otherwise, it returns the slope between the two points.

NEXT STEPS: What else do you want to program?
We’ve shown you an example of how to integrate computational thinking by programming on the TI-Nspire CX handheld, but there are many other types of explorations to do with coding on your calculator. Exploring calculation-type programs like the one above gives students an introduction to coding, yet retains the fidelity of your core math subject. There are many other examples you may want your students to try: determining the equation of a line between two points, calculating the length of any leg of a right triangle from the other two, or displaying the roots of a quadratic given in standard form. All of these calculation-type programs give students an opportunity to reinforce their knowledge and deepen their understanding of those relationships, and exposes them to writing code for mathematical processes. There are other types of programs students could write that model recursive mathematics and other deeper topics. Let’s face it – students who are writing code to perform operations are deepening their understanding of the underlying mathematics. And remember, if they can code it, then they know it.
Happy coding!
Tagcloud
Archive
- 2026
- 2025
- 2024
- 2023
- 2022
-
2021
- January (1)
- February (3)
- March (5)
-
April (7)
- Top Tips for Tackling the SAT® with the TI-84 Plus CE
- Monday Night Calculus With Steve Kokoska and Tom Dick
- Which TI Calculator for the SAT® and Why?
- Top Tips From a Math Teacher for Taking the Online AP® Exam
- Celebrate National Robotics Week With Supervised Teardowns
- How To Use the TI-84 Plus Family of Graphing Calculators To Succeed on the ACT®
- AP® Statistics: 6 Math Functions You Must Know for the TI-84 Plus
- May (1)
- June (3)
- July (2)
- August (5)
- September (2)
-
October (4)
- Transformation Graphing — the Families of Functions Modular Video Series to the Rescue!
- Top 3 Halloween-Themed Classroom Activities
- In Honor of National Chemistry Week, 5 “Organic” Ways to Incorporate TI Technology Into Chemistry Class
- 5 Spook-tacular Ways to Bring the Halloween “Spirits” Into Your Classroom
- November (4)
- December (1)
- 2020
- 2019
-
2018
- January (1)
- February (5)
- March (4)
- April (5)
- May (4)
- June (4)
- July (4)
- August (4)
- September (5)
- October (8)
-
November (8)
- Testing Tips: Using Calculators on Class Assessments
- Girls in STEM: A Personal Perspective
- 5 Teachers You Should Be Following on Instagram Right Now
- Meet TI Teacher of the Month: Katie England
- End-of-Marking Period Feedback Is a Two-Way Street
- #NCTMregionals Kansas City 2018 Recap
- Slope: It Shouldn’t Just Be a Formula
- Hit a high note exploring the math behind music
- December (5)
- 2017
- 2016
- 2015
