Education Technology
Sign Up for TI Emails

How To Use the TI-84 Plus Family of Graphing Calculators To Succeed on the ACT®

Posted 04/02/2021 by Jeff McCalla, St. Mary’s Episcopal School Math Teacher (@jmccalla1)

Standardized tests have a way of asking questions that go past number crunching, and dive into the concepts. Often, these questions reveal misconceptions that students may have or just introduce a topic that the students haven’t really had a chance to explore. The fascinating part is that usually the questions cover common topics, but the tests take an uncommon approach to asking the question.

I am going to share two ACT® questions that do precisely that. They challenge you to think differently about solving problems. I am a math teacher (and the test-prep coordinator) at St. Mary’s Episcopal School in Memphis. I enjoy the challenge of preparing students to tackle these demanding questions.

In high school algebra, quadratics are studied extensively. Even so, this question is most likely one that students haven’t spent much time thinking about. In fact, how do you think about it? Graphing on the TI-84 Plus CE graphing calculator can help students visualize the mathematics in a way that I have trouble showing with pencil and paper. Below is the question:


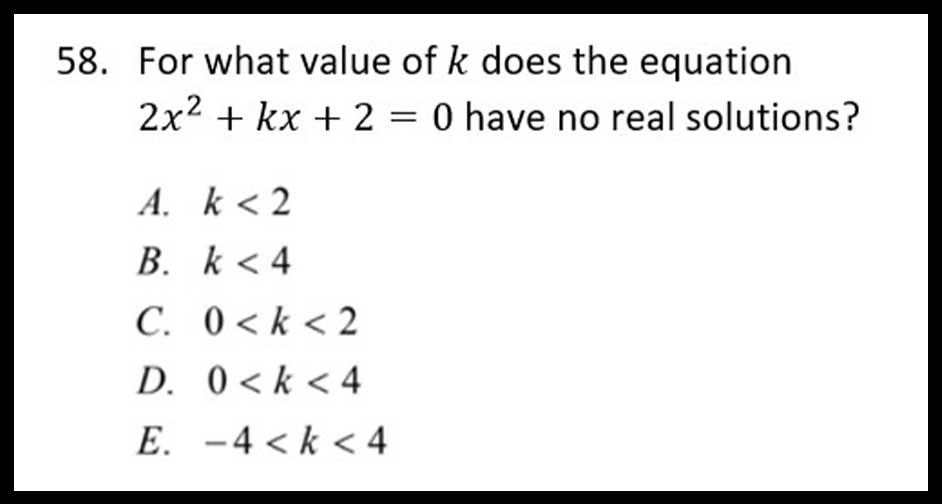
The standard form of a quadratic is ax^2+bx+c. High school students have observed the effect of a (vertical stretch/shrink and reflection over the x-axis) as well as the effect of c (y-intercept). But, the effect that b has on the graph of a quadratic? Not so much.

Using the recently improved Transformation app on the TI-84 Plus CE provides an illustration of the movement that changing the value of b has on the graph. Here are the steps to graph the function using the Transformation app:
  1. Press Œ} and choose the Transfrm to start the app running.
  2. Press o and enter the function in the problem, making sure that you enter b instead of k for the variable.
  3. Press s and us the | and ~ arrow keys to change the value of b.
  4. Set b = 0 and make observations about the graph.


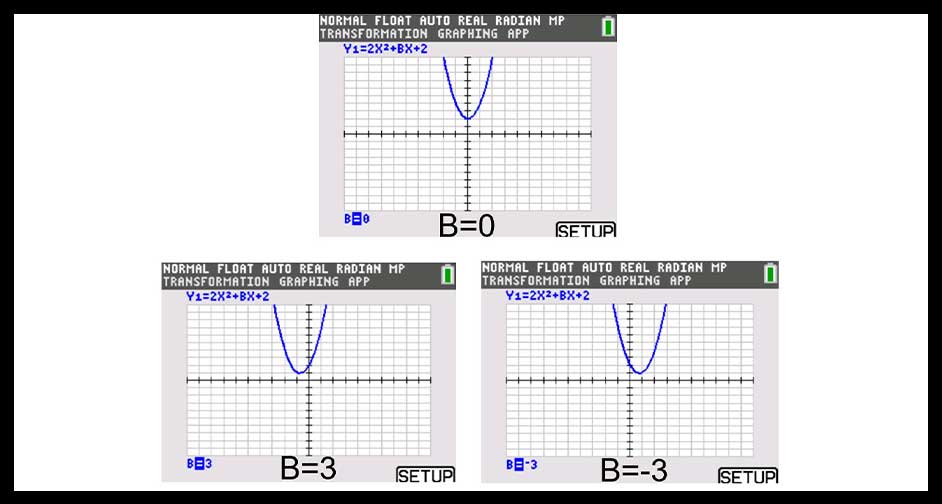
What I like students to discover is that the axis of symmetry will be on the y-axis whenever b=0. And, that the graph moves in a symmetrical fashion about the y-axis as the value of b changes. In fact, when B = 3, the graph when B = -3 is a reflection across the y-axis.

Press s to access the SETUP menu, and turn the TrailOn. This feature allows you to see a remnant of the movement that the graph makes as the value of b changes.


How does that help answer this question? If you know that the axis of symmetry is on top of the y-axis when b = 0 and the graph moves in a symmetrical fashion, well, answer choice E (-4>k<4) is the only answer choice that is symmetric around the value of zero, so it must be the answer. If you learned the concept, you don’t even have to see the graph to know the answer. No calculations are necessary.

Of course, I would be pretty happy if a student thought to use the value of the discriminant in order to find which values for b would yield no solutions for the quadratic. I’m convinced too many students are just memorizing steps. In order to use the discriminant to find out how many and what type of solutions a quadratic has, I want students to picture the discriminant as part of the quadratic formula. If the discriminant is negative, then the square root of a negative will always produce an imaginary solution.


I am often surprised on which questions students have trouble with. I think I tend to have an overly optimistic view of students’ math abilities and understandings. I can assure you that this next problem gives students fits. It doesn’t look that tough, but I think it uncovers a misunderstanding that many students have when working with trig ratios. Here it is:


When students learn SohCahToa they are told that the “o” stands for opposite side, “a” for the adjacent side, and “h” for the hypotenuse. So, when students see cos⁡(D) = 5/8, they immediately think that the adjacent side is 5, and the hypotenuse is length 8. This is a super-confusing problem for a couple of reasons. The adjacent side is already labeled 9, and none of the answer choices for the length of segment DF are 8? It boils down to students not understanding that sine, cosine and tangent are RATIOS. In other words, the numerator is not necessarily the length of the adjacent side when calculating the cosine, and so on.

So, how could we introduce the concept of trig ratios so that the students get the concept? I like to use technology as an exploratory tool for students. Once students learn that sine is the ratio of the opposite side to the hypotenuse, show them the image below and have them use their TI-84 Plus CE to calculate the sine of the three angles (65°,75° and 85°). Ask them:
  1. What do you think the sine of 90° would be?
  2. Test your conjecture by finding the sine of (88°,89° and 90°).
  3. Why is the sine of 90° the limit for how big the sine of an angle can be?


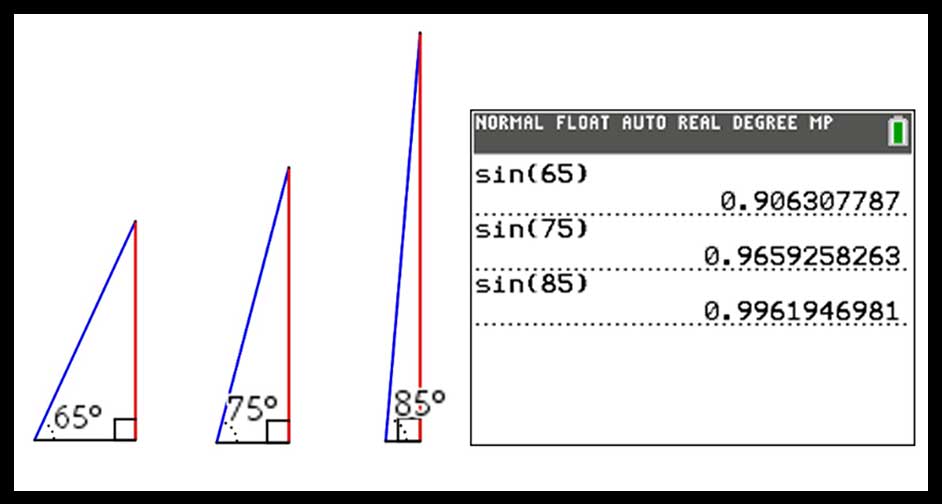
By taking the numerator and denominator out of the discussion, students may be able to see the concept that the ACT® question so masterfully incorporated into their question.

Pretty neat, huh? Getting to know your TI-84 Plus CE can pay off in a big way on the ACT® exam. If you are a teacher and interested in learning more about both the TI-84 Plus CE and the ACT®, check out the offerings in the Professional Development tab of education.ti.com.


ACT is a registered trademark of ACT, Inc., which does not endorse TI products. Policies subject to change. Visit www.act.org.


About the author: Jeff McCalla, author of “TI-84 Plus Graphing Calculator for Dummies,” 2nd ed. (Wiley, 2013) and “TI-Nspire for Dummies,” 2nd ed. (Wiley, 2011), teaches math at St. Mary’s Episcopal School in Memphis. McCalla received the Presidential Award of Excellence in Mathematics and Science Teaching in 2009. Follow him on Twitter @jmccalla1.

Tags:

Tagcloud

Math STEM coding classroom resources TI-84 Plus CE science Python graphing calculator TI-Nspire CX II activity STEM and coding TI Back To School high school calculus TI-84 Plus CE graphing calculator computer science calculator school

Archive

Syndication

© Copyright 1995-2024 Texas Instruments Incorporated. All rights reserved.

TrademarksSoftware Data PolicyPrivacy PolicyCookie PolicyTerms of UseTerms of Sale & ServicesSupply Chain Transparency
About UsNews CenterContact TI