Intuition, Confidence, Simulation, Calculation: The MonTI Hall Problem and Python on the TI-Nspire™ CX II Graphing Calculator
Posted 10/28/2022 by Steve Phelps (@MathTechCoach)
Origins of the Monty Hall problems
“Let’s Make a Deal” was a variety game show that started in 1963 and was co-created and co-produced by Monty Hall. The format of “Let’s Make a Deal” involves selected members of the studio audience making deals with the host. The audience member would typically be offered something of value and given a choice of whether to keep it or exchange it for a different item that may or may not be of greater value.
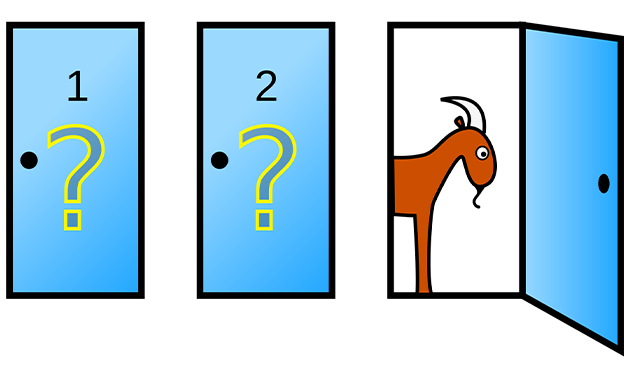
The Monty Hall problem is presented as a probability puzzle loosely based on this show and named after its original host, Monty Hall. The puzzle is presented like this:
|
You are given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door and the host, who knows what’s behind the doors, opens another door which has a goat. He then says to you, “Do you want to switch your pick to the unopened door?”
Is it to your advantage to switch your choice? |
If you know about this problem and you know the answer, feel free to skip ahead!
An instructional arc for teaching probability
Probability is one of those content areas that seems to get pushed to the end of the year, right before state testing. With the time crunch, the focus for teaching probability tends to fall on calculation instead of helping students to develop a sense of randomness. Just about any mathematics topic can have a degree of randomness inserted without sacrificing content. Furthermore, it’s that randomness that catches the interest of the students and gives them an opportunity to be invested in the outcome.
How can we accomplish this? By following the instructional arc of
- Intuition
- Confidence
- Simulation
- Calculation
This instructional arc is a mashup of an instructional arc I learned from Allan Rossman years ago at Serenbe down in Georgia and from playing the dice game Borel with my students.
Intuition
Intuition is all about giving kids a chance to stake a claim as to how likely or unlikely a random outcome is. It is all about what your gut tells you! Is it certain? Very likely? Somewhat likely? Somewhat unlikely? Very unlikely? Will not happen? For the Monty Hall problem, it is what you think is the answer to the question. Notice I am not asking for a number or a probability or a percentage. Just a degree of likeliness.
For the Monty Hall problem, it is about what your gut is telling you about switching doors. Should you switch doors? Or should you stick with the door you chose? Or does it even matter? Make a commitment to one of these answers by writing it down.
Confidence
How confident are you in what your gut is telling you? This could be on a scale from 1 (not confident) to 4 (very confident). Or it could be in the form of a “stat coin” wager. Would you wager 800 stat coins? 400 stat coins? 200? 100?
On a scale of 1 (not confident) to 4 (very confident), how confident are you in your answer to the question “should you switch doors?” Make a commitment to your answer by writing it down!
Simulation
Simulations give students and adults alike the opportunity to revise their original intuition as a result of experiencing a number of single simulated outcomes using the TI-84 Plus CE Python or the TI-Nspire™ CX II graphing calculators. You could generate random numbers on either handheld to simulate the rolls of dice. And now, you can write powerful and quick Python scripts on either graphing calculator to explore random outcomes of thousands of trials.
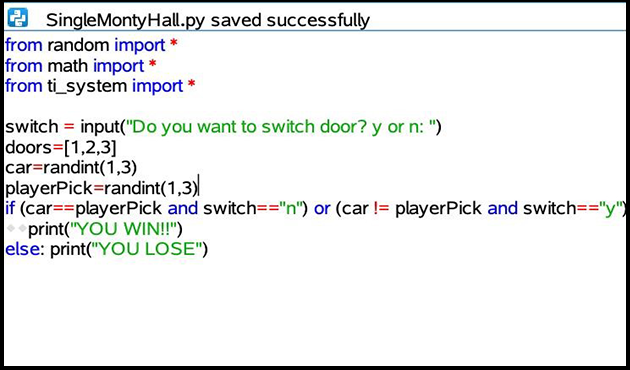
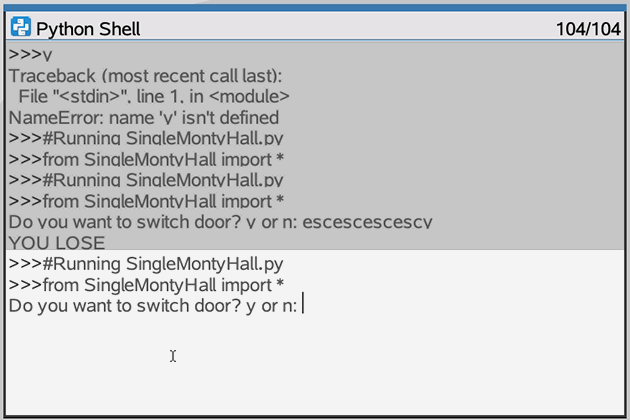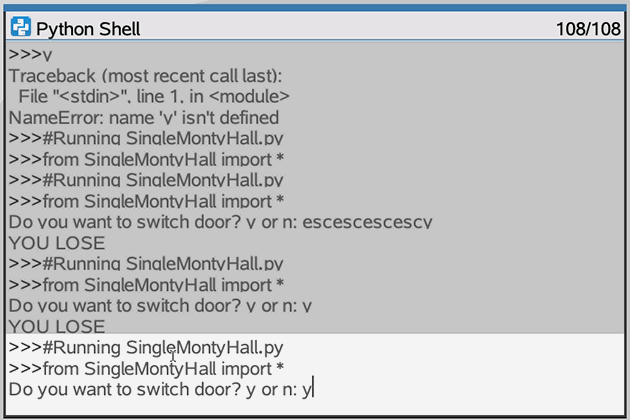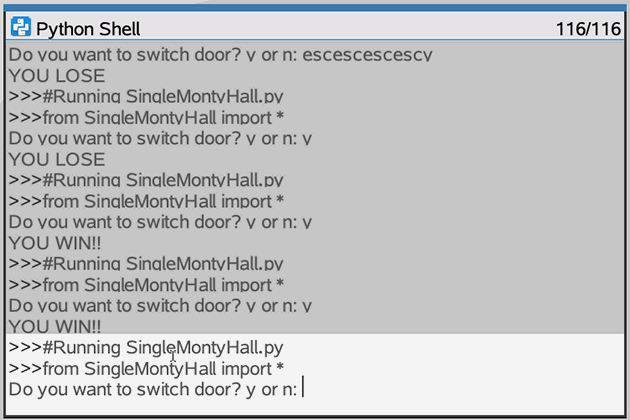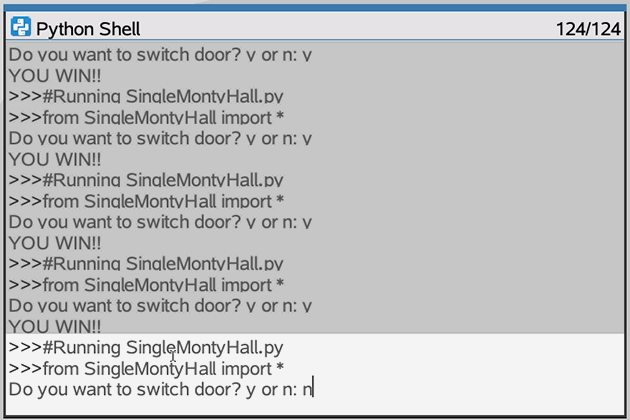
Here is a simulation that will run one trial of the Monty Hall simulation, prompting you about switching or not. Thinking about the game, you will win if you originally pick the door where the car is and you decide not to switch. You will also win if you originally pick a door with a goat and you switch to the unopened door, which must have the car behind it. This is the logic behind the IF statement on line 9 in the code below.
if (car==playerPick and not switch) or (car != playerPick and switch):
Based upon the results of this once-at-a-time simulation, do you want to revise your initial response to the problem? Are you surprised? Perhaps more — many more — trials are in order.
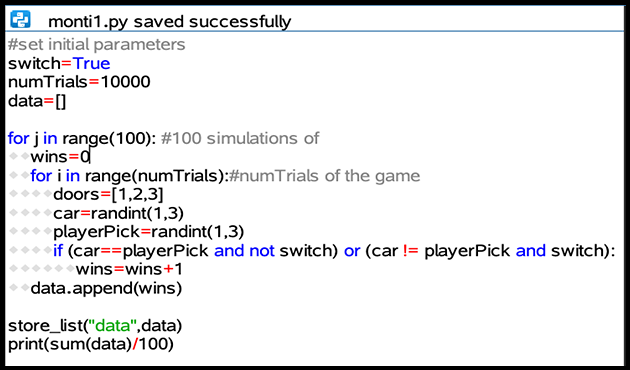
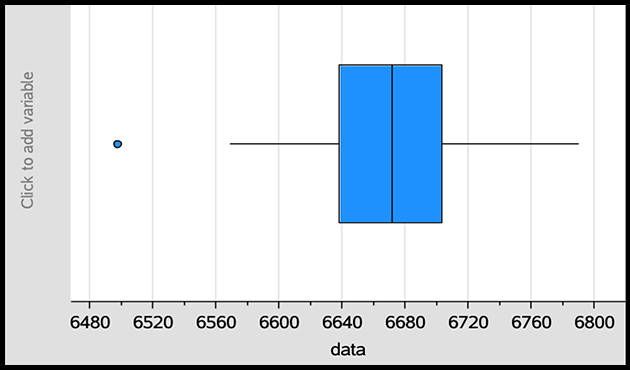
In this simulation, we run the single Monty Hall simulation 10,000 times. Our choice is to always switch (switch = True). We will repeat this 10,000 trial simulation 100 times and plot the resulting number of wins out of 10,000 trials each time. We appear to win 6,669.69 times on average out of 10,000 trials. You can change the switch variable to False in order to not switch during the simulation.
As you can see in the dot plot of the results, each dot in the plot represents the number of times you win by switching in each of the 10,000 Monty Hall simulations. Even though there is an outlier, most of the dots seem to be clustered around 6,670 wins (the mean number of wins out of 10,000 single Monty Hall simulations is 6,669.69 wins).
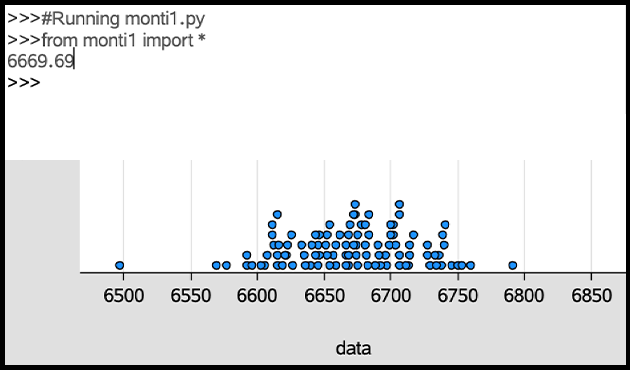
In fact, the middle 50% of wins falls between approximately 6,640 wins and 6,700 wins.
Calculation
This is the last step in the instructional arc of teaching probability, and I think it should be the last step since, in many ways, this might be the least important step when it comes to helping a student develop their reasoning about probability and randomness.
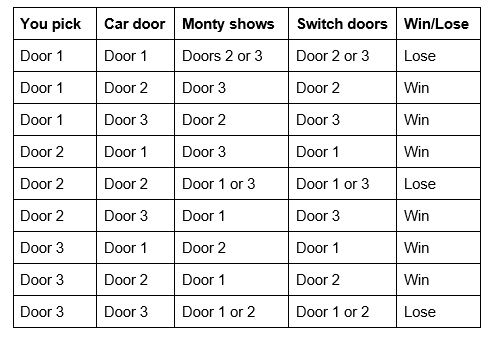
Calculations do not always need to be carried out by hand. An easy way to see that you win the car ⅔ of the time by switching doors is by a tree diagram or a chart. In this chart, we can analyze all nine scenarios that could occur and when you win (or lose) by switching doors. You can see that you win six out of nine times. Ultimately, you only lose if you pick the car door to start (unknown to you) with and switch away from it (also unknown to you).
Conclusion
The Monty Hall problem is one of those probability puzzles that is easy to understand. Its paradoxical nature is surprising as well as counterintuitive, and that is one of the hooks that captures students’ attention. Most people (adults and students) experiencing this problem for the first time think the probability of winning when you switch in just ½. Even after listing all nine possible outcomes, it is still hard to believe the true probability of winning when switching doors is ⅔. With Python on the TI-Nspire™ CX II graphing calculator, students can be guided to create a Python program to run thousands of simulations quickly and can help to convince them that the probability of winning is indeed ⅔. Check out the one we used here for the Monty Hall problem. Download the .tns file for the Monty Hall problem.
If you were intrigued by this blog and wish to learn more about how to use the Monty Hall problem in your classroom, check out the on-demand webinar “Let’s Make a Deal — Exploring the MonTI Hall Problem and Its Variations.”
About the author: Steve Phelps is a T³™ National Instructor and is entering his 32nd year in education. After serving the past three years as an instructional technology consultant for the Hamilton County ESC, he has moved into a new role as an instructional technology coach, a math coach, and a math and computer science teacher for Mariemont City Schools in Cincinnati. He is active on Twitter (@MathTechCoach) where you can connect with him there.
