Lesson 13.2: The First Derivative Test
In previous modules you have seen the relationship between a function and its first derivative. In this lesson you will use this relationship to determine the behavior of a function at its critical points and endpoints.
The sign of the first derivative on either side of a critical point can be used to determine whether the critical point is a local maximum, a local minimum or neither. The following discussion describes how the first derivative, when evaluated around a critical point, is related to local maxima and minima.
The First Derivative Test
The First Derivative Test consists of three parts: using the first derivative when testing for local maxima, when testing for local minima, and when identifying critical points that are neither. Additionally, the nature of endpoints may also be determined by using the first derivative. Collectively, the parts are called the first derivative test. Each part is discussed below and is then stated formally.
The First Derivative Test to Find a Local Maximum
Recall that the first derivative represents the slope of the tangent line to the curve. The diagram below shows a function near a critical point, which is represented by the vertical line. The plus and minus signs indicate where the function's first derivative is positive and where it is negative. Notice that when the first derivative is positive, the slopes are positive and the function is increasing. When the first derivative is negative, the slopes are negative and the function is decreasing. If the derivative changes from positive to negative at the critical point, the critical point is a local maximum
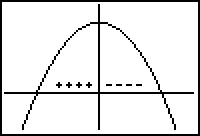
Part I If the first derivative is positive to the left of a critical point and negative to the right of the critical point, then f has a local maximum at the critical point.
The First Derivative Test to Find a Local Minimum
The first derivative of the function shown below has negative values left of the critical point and positive values right of the critical point, as indicated by the diagram. The critical point is a local minimum.
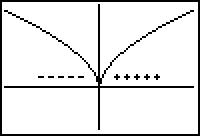
Part II If the first derivative is negative to the left of a critical point and positive to the right of the critical point, then f has a local minimum at the critical point
The First Derivative Test for Neither
As discussed at the end of Lesson 13.1, x = 0 is a critical point of f(x) = x3 but there is no local extremum there. It was noted that the first derivative (slope of the tangents) is positive on both sides of the critical point, so the sign of the derivative does not change from one side of x = 0 to the other.
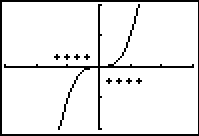
The general statement about the sign of the derivative at non-extreme points is given below.
Part III If the first derivative has the same sign on both sides of the critical point, then the function does not have a local maximum or a local minimum at the critical point.
Extrema at Endpoints
A function's first derivative can only be evaluated on one side of an endpoint of a function's domain. Whether an endpoint is a local maximum or minimum is determined by the sign of the first derivative when evaluated just inside the domain near the endpoint.
Local Extrema at a Left Endpoint
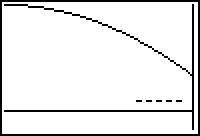
If the first derivative is positive to the right of a left endpoint, the function has a local minimum at the left endpoint. If the derivative is negative to the right of a left endpoint, the function has a local maximum at the left endpoint. The diagrams below illustrate a left endpoint that is a local minimum and a left endpoint that is a local maximum.
Recall that a function is increasing when the slope of a tangent line is positive and decreasing when the slope of a tangent line is negative. The plus and minus signs indicate the sign of the first derivative, which also represents the slope of the tangent lines and indicate whether the function is increasing or decreasing.
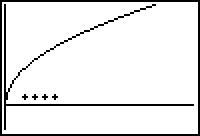

The First Derivative Test at a Right Endpoint
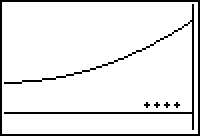
If the first derivative is negative to the left of a right endpoint, the function has a local minimum at the right endpoint. If the derivative is positive to the left of a right endpoint, the function has a local maximum at the right endpoint.
The diagrams below illustrate a right endpoint that is a local minimum and a right endpoint that is a local maximum. Again, the plus and minus signs indicate the sign of the first derivative and indicate whether the function is increasing or decreasing.
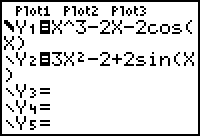
Extreme Values of f(x) = x3 - 2x - 2cos (x)
Use the First Derivative Test to find the extreme values of f(x) = x3 - 2x - 2cos(x).
The domains of f(x) = x3 - 2x - 2cos(x) and f'(x) = 3x2 - 2 + 2sin(x) are the set of all real numbers, so there are no endpoints to consider and there are no values at which f ' does not exist.
- Set Y1 =X^3 - 2X - 2 cos(X) and Y2=3X^2 - 2 + 2sin(X)
- Set the graphing style of Y1 to thick and graph the function and its derivative in a [-3, 3, 1] x [-5, 5, 1] window.
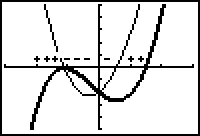
The graph illustrates that f ' has a zero that is a little less than -1 and a zero that is about 0.5.
Because the sign of f ' changes from positive to negative at the zero of f ' that is less that -1, the first derivative test says that the function f has a local maximum at this value of x.
Similarly, the sign of f ' goes from negative to positive at the zero of f ' that is about 0.5, so the first derivative test says that the function f has a local minimum at this value of x.
The zeros of f ' may be approximated using the CALCULATE menu's Zero feature.
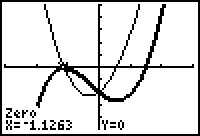
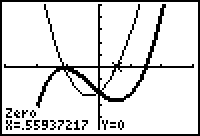
The zero that is a little less than -1 is approximately -1.126 and the other zero is approximately 0.559.
According to the first derivative test, the function has a local maximum at x
![]() -1.126 and a local minimum at x
-1.126 and a local minimum at x
![]() 0.559, which is supported by the function's graph.
0.559, which is supported by the function's graph.
13.2.1 Using the calculator's Value feature, find the y-values at the local maximum and minimum of f(x) = x3 - 2x -2cosx? Click here for the answer.
