Lesson 13.3: The Second Derivative Test
In this lesson you will learn about the second derivative test. The second derivative test is an alternative to the first derivative test for analyzing critical points where the first derivative is zero. Recall that the second derivative describes concavity. If the graph of f(x) is concave upward or concave downward at a point where the graph has a horizontal tangent line, then there is a local minimum or local maximum, respectively, at that point.
Lesson 11.2 described the relationship between a second derivative and a function. It was found that:
- when the second derivative is positive the function is concave upward,
- when the second derivative is negative the function is concave downward,
These facts can sometimes be used to determine if a critical point is a local maximum or a local minimum. At a critical point where the first derivative is zero:
- If the second derivative is positive at the point, the function is concave upward there and the critical point is a local minimum.
- If the second derivative is negative at the point, the function is concave downward there and the critical point is a local maximum.
These concepts of local maximum and local minimum are illustrated below.

|
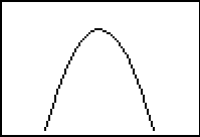
|
| Local minimum because concave upward | Local maximum because concave downward |
The second derivative test described above is formally stated below.
The Second Derivative Test
Suppose f is a twice differentiable function and c is in the domain of f.
- If f'(c) = 0 and f"(c) < 0, then f is concave down and has a local maximum at x = c.
- If f'(c) = 0 and f"(c) > 0, then f is concave up and has a local minimum at x = c.
The Local Extrema of f(x) = x3 - 2x - 2cos x
In Lesson 13.2 we found the local extrema of f(x) = x3 - 2x - 2cos x using the first derivative test. Now we will apply the second derivative test to the problem.
- Set Y1=X^3 - 2X - 2 cos(X) and Y2= 6X + 2 cos(X), which is the second derivative of Y1.
-
Set the graphing style of Y1 to thick and graph the function and its second derivative in a
[-3, 3, 1] x [-5, 5, 1] window.

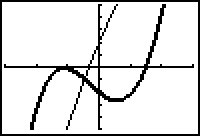
In Lesson 13.2 we found the critical points where f'(x) = 0 were x
![]() -1.126 and x
-1.126 and x
![]() 0.559.
0.559.
- Evaluate the second derivative at x = -1.126 and x = 0.559 by entering Y2(-1.126) and Y2(0.559) on the Home screen.
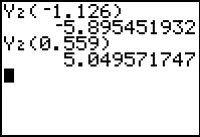
Conclusions about the critical points are summarized below.
- Because f'(-1.126) = 0 and f"(-1.126) < 0, f has a local maximum at x = -1.126.
- Because f'(0.559) = 0 and f"(0.559) > 0, f has a local minimum at x = 0.559.
If f "(c) = 0 at the critical point, then one cannot draw any conclusion. The second derivative test cannot be used for critical points where the first derivative is undefined.
13.3.1 Use the second derivative test to find the local extrema of f(x) = x3 - 3x + 5. Click here for the answer.
