Extreme Values of Functions
Answers
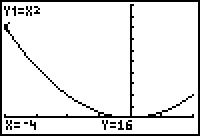
As shown in the previous example, the function has only one critical point, which occurs at x = 0. The values of the output at the critical point and at the endpoints are f(-4) = 16, f(0) = 0 and f(2) = 4.
The function has:
- an absolute and a local maximum of 16 at x = -4,
- an absolute and a local minimum of 0 at x = 0, and
- a local maximum of 4 at x = 2.
The graph below, shown in a [-4, 2, 1] x [-2, 20, 2] window, supports the conclusions.
The first derivative of the function is f'(x) = 3x2 - 3. The critical points are x = -1 and x = 1 because f'(-1) = 0 and f'(1) = 0.
The second derivative of the function is f"(x) = 6x. The second derivative evaluated at the critical points yields f"(-1) < 0 and f"(1) > 0.
Therefore, f has a local maximum at x = -1 and a local minimum at x = 1. The y-value at the local maximum is 7, and the y-value at the local minimum is 3. These are found by evaluating f(-1) and f(1) respectively.
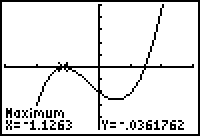
The local maximum occurs at approximately (-1.1263, -0.0362). Depending on what you select for the bounds and the initial guess, the x-coordinate shown on your screen might differ slightly from the one shown in the graph above.
The absolute maximum of 4 occurs at x = 0.
The absolute and local minimum of approximately 2.680 occurs at x = 2.
A local minimum of 3 occurs at x = -1.
