Vertical and Phase Shifts

Author

Texas Instruments

Alignment

Standards Alignment

Textbook Alignment

Subject Area

Math: Precalculus: Trigonometry (Triangle and Circular Functions)

Level

9-12

Activity Time

45 Minutes

TI Calculator

TI-Nspire™ CX series

TI-Nspire™ CX CAS/CX II CAS

TI-Nspire Version

3.2

Resource Types

Lessons

Format

TNS

Report an Issue

Vertical and Phase Shifts

Activity Overview

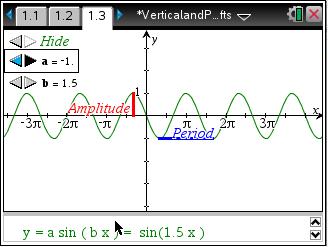
Students explore vertical and phase shifts of sine and cosine functions and determine the effect that each change has upon the shape of the graph.

Download Files

Download All Files (ZIP)

Teacher Files

Teacher Notes PDF

Student Files

Student Activity DOC Student Activity PDF TI-Nspire Activity TNS

Author

Texas Instruments

Alignment

Standards Alignment

Textbook Alignment

Subject Area

Math: Precalculus: Trigonometry (Triangle and Circular Functions)

Level

9-12

Activity Time

45 Minutes

TI Calculator

TI-Nspire™ CX series

TI-Nspire™ CX CAS/CX II CAS

TI-Nspire Version

3.2

Resource Types

Lessons

Format

TNS

Report an Issue

iPad is a trademark of Apple Inc., registered in the U.S. and other countries.
Vernier EasyData,Vernier EasyLink and Vernier EasyTemp are registered trademarks of Vernier Science Education.

Control your cookie preferences

You can control your preferences for how we use cookies to collect and use information while you're on TI websites by adjusting the status of these categories.

Category	Description	Allow
Analytics and performance cookies	These cookies, including cookies from Google Analytics, allow us to recognize and count the number of visitors on TI sites and see how visitors navigate our sites. This helps us improve the way TI sites work (for example, by making it easier for you to find information on the site).
Advertising and marketing cookies	These cookies enable interest-based advertising on TI sites and third-party websites using information you make available to us when you interact with our sites. Interest-based ads are displayed to you based on cookies linked to your online activities, such as viewing products on our sites. We may also share this information with third parties for these purposes. These cookies help us tailor advertisements to better match your interests, manage the frequency with which you see an advertisement, and understand the effectiveness of our advertising.
Functional cookies	These cookies help identify who you are and store your activity and account information in order to deliver enhanced functionality, including a more personalized and relevant experience on our sites. If you do not allow these cookies, some or all site features and services may not function properly. If you do not allow these cookies, some or all of the site features and services may not function properly.
Social media cookies	These cookies allow identification of users and content connected to online social media, such as Facebook, Twitter and other social media platforms, and help TI improve its social media outreach.
Strictly necessary	These cookies are necessary for the operation of TI sites or to fulfill your requests (for example, to track what items you have placed into your cart on the TI.com, to access secure areas of the TI site, or to manage your configured cookie preferences).	Always On

Category

Description

Allow

Analytics and performance cookies

These cookies, including cookies from Google Analytics, allow us to recognize and count the number of visitors on TI sites and see how visitors navigate our sites. This helps us improve the way TI sites work (for example, by making it easier for you to find information on the site).

Advertising and marketing cookies

These cookies enable interest-based advertising on TI sites and third-party websites using information you make available to us when you interact with our sites. Interest-based ads are displayed to you based on cookies linked to your online activities, such as viewing products on our sites. We may also share this information with third parties for these purposes. These cookies help us tailor advertisements to better match your interests, manage the frequency with which you see an advertisement, and understand the effectiveness of our advertising.

Functional cookies

These cookies help identify who you are and store your activity and account information in order to deliver enhanced functionality, including a more personalized and relevant experience on our sites. If you do not allow these cookies, some or all site features and services may not function properly.

Social media cookies

These cookies allow identification of users and content connected to online social media, such as Facebook, Twitter and other social media platforms, and help TI improve its social media outreach.

Strictly necessary

These cookies are necessary for the operation of TI sites or to fulfill your requests (for example, to track what items you have placed into your cart on the TI.com, to access secure areas of the TI site, or to manage your configured cookie preferences).

Always On

Vertical and Phase Shifts

Vertical and Phase Shifts

Control your cookie preferences

Products

Product Support

Teacher Resources

Administrator Resources

Lessons and Activities

General Information