Lesson 13.1: Critical Points
In this lesson, you will learn about absolute and local extreme values, and identify extreme values from the set of critical points and endpoints.
Optimization problems are one of the most important applications of differential calculus because we often want to know when the output of a function is at its maximum or minimum. In such problems there may be a largest or smallest output value over the entire input interval of interest or within a local neighborhood of an input value. Both absolute and local maximum and minimum values are of interest in many contexts.
Absolute Extreme Values of a Function
When an output value of a function is a maximum or a minimum over the entire domain of the function, the value is called the absolute maximum or the absolute minimum, as defined below.
Let f be a function with domain D and let c be a fixed constant in D. Then the output value f(c) is the
-
absolute maximum value of f on D if and only if f(x)
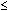 f(c) for all x in D.
f(c) for all x in D.
-
absolute minimum value of f on D if and only if f(c)
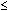 f(x) for all x in D.
f(x) for all x in D.
Absolute Extreme Values - An Example
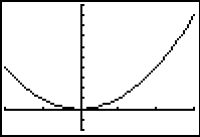
The domain of f(x) = x2 is all real numbers and the range is all nonnegative real numbers. The graph in the figure below suggests that the function has no absolute maximum value and has an absolute minimum of 0, which occurs at x = 0.
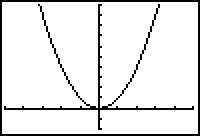
The Absolute Extreme Values on a Restricted Domain
If the domain of f(x) = x2 is restricted to [-2, 3], the corresponding range is [0, 9]. As shown below, the graph on the interval [-2, 3] suggests that f has an absolute maximum of 9 at x = 3 and an absolute minimum of 0 at x = 0.
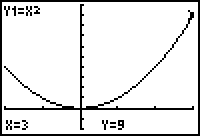
The two examples above show that the existence of absolute maxima and minima depends on the domain of the function.
Extreme Value Theorem
Theorem 1 below is called the Extreme Value theorem. It describes a condition that ensures a function has both an absolute minimum and an absolute maximum. The theorem is important because it can guide our investigations when we search for absolute extreme values of a function.
Theorem 1 If f is continuous on a closed interval [a, b], then f has both an absolute maximum value and an absolute minimum value on the interval.
This theorem says that a continuous function that is defined on a closed interval must have both an absolute maximum value and an absolute minimum value. It does not address how to find the extreme values.
Local Extreme Values of a Function
One of the most useful results of calculus is that the absolute extreme values of a function must come from a list of local extreme values, and those values are easily found using the first derivative of the function.
Local extreme values, as defined below, are the maximum and minimum points (if there are any) when the domain is restricted to a small neighborhood of input values.
Let c be an interior point of the domain of the function f. Then the function f has a
-
local maximum at c if and only if f(x)
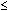 f(c) for all x in some open interval containing c.
f(c) for all x in some open interval containing c.
-
local minimum at c if and only if f(c)
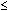 f(x) for all x in some open interval containing c.
f(x) for all x in some open interval containing c.
Endpoints as Local Extrema
The definition of local extrema given above restricts the input value to an interior point of the domain. The definition can be extended to include endpoints of intervals.
It is clear from the definitions that for domains consisting of one or more intervals, any absolute extreme point must also be a local extreme point. So, absolute extrema can be found by investigating all local extrema.
Candidates for Local Extreme-Value Points
Theorem 2 below, which is also called Fermat's Theorem, identifies candidates for local extreme-value points.
Theorem 2 If a function has a local maximum value or a local minimum value at an interior point c of its domain and if f ' exists at c, then f ' (c) = 0.
Finding Extreme Values of a Function
Theorem 2 says that if a function has a first derivative at an interior point where there is a local extremum, then the derivative must equal zero at that point. It does not say that every point where the first derivative equals zero must be a local extremum. Because of Theorem 2, only a few points need to be considered when finding a function's extreme values. Those points consist of interior domain points where f ' (x)= 0, interior domain points where f ' does not exist, and the domain's endpoints, which are not covered by the theorem.
Critical Points
A critical point is an interior point in the domain of a function at which f ' (x) = 0 or f ' does not exist. So the only possible candidates for the x-coordinate of an extreme point are the critical points and the endpoints.
Finding the Extreme Values Using Calculus Techniques
Find the local and absolute extreme values of f(x) = x2 on the closed interval [-2, 3] using calculus. Theorem 1 applies here, so we know for certain that this function must have absolute extrema on this domain.
Note the following:
- f ' (x) = 2x, which is zero only at x = 0 and exists at all values of f in [-2, 3]. Therefore, x = 0 is the only critical point of f.
- The values of f at the endpoints are f(-2) = 4 and f(3) = 9.
By comparing the output values when x = -2, x = 0, and x = 3, the absolute extrema may be determined.
- f has a local minimum of 0 at x = 0, which is also an absolute minimum.
- f has a local maximum of 4 at x = -2 and a local maximum of 9 at x = 3. The absolute maximum of f is 9.
Review the graph of the function on the restricted domain. The graph supports the above results.
13.1.1 Find the extreme values of f(x) = x2 on [-4, 2] using calculus techniques and then support your answers by sketching the graph. Click here for the answer.
Calculus techniques produce results that may be supported by graphs, and graphs can guide in the discovery of extreme values, as shown in the next example.
Extreme Values of f(x) = x2/3 on [-2, 4]
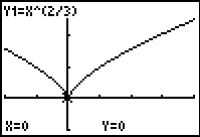
Find the extreme values of f(x) = x2/3 on the restricted domain [-2, 4] by viewing the graph and then using calculus techniques.
- Enter X^(2/3) in Y1.
- Display the graph in a [-2, 4,1] x [-1, 3,1] window.

The function appears to have an absolute minimum near x = 0 and two local maximums, which occur at the endpoints of the restricted domain. The absolute maximum occurs at the right endpoint of the restricted domain.
Now determine the extreme points using calculus techniques.
- Use the power rule to find f ':
The derivative,
![]() , is not equal to 0 anywhere on [-2, 4], so no critical point comes from that condition, but f ' does not exist at x = 0, which implies that x = 0 is a critical point. Therefore, the only critical point of f occurs at x = 0.
, is not equal to 0 anywhere on [-2, 4], so no critical point comes from that condition, but f ' does not exist at x = 0, which implies that x = 0 is a critical point. Therefore, the only critical point of f occurs at x = 0.
Use the Graph screen's Value feature to compute the values of f at the critical point and at the endpoints of the restricted domain [-2, 4].
-
From the graph of f press
 [CALC] and select 1:value.
[CALC] and select 1:value.
- Evaluate f at x = -2, x = 0, and x = 4 by entering -2, 0, and 4, respectively.
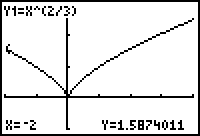
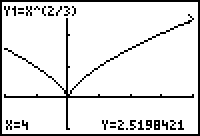
The extreme values can be summarized as follows:
- f has a local and absolute minimum of 0 at 0.
- The value of f at x = -2 is approximately 1.587 and the value at x = 4 is approximately 2.520. Each is a local maximum value.
- The absolute maximum value of f is approximately 2.520 at x = 4.
Extreme Values of
![]()
In the previous examples, we have been dealing with continuous functions defined on closed intervals. In such a case, Theorem 1 guarantees that there will be both an absolute maximum and an absolute minimum. In this example, the domain is not a closed interval, and Theorem 1 doesn't apply. The extreme values of
![]() may be found by using a procedure similar to that above, but care must be taken to ensure that extrema truly exist.
may be found by using a procedure similar to that above, but care must be taken to ensure that extrema truly exist.
Notice that the domain of f is (-2, 2) because the radicand must be non-negative and the denominator must be non-zero.
-
Graph
 in a [-4, 4, 1] x [-2, 4, 1] viewing window.
in a [-4, 4, 1] x [-2, 4, 1] viewing window.
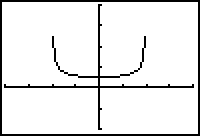
The graph suggests there is an absolute minimum of about 0.5 at x = 0. There also appear to be local maxima of about 2.5 when x = -2 and x = 2. However, f is not defined at x = -2 and x = 2, so they cannot be local maxima.
Calculus techniques require that the endpoints of the domain and critical points must be identified. The domain of f is (-2, 2), an open interval, so there are no endpoints. Critical points are determined by using the derivative, which is found with the Chain Rule.
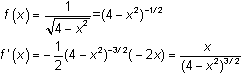
The derivative is 0 at x = 0 and it is undefined at x = -2 and x = 2. Because -2 and 2 are not in the domain of f, the only critical point is x = 0.
As x moves away from 0 in either direction, the denominator of f(x) gets smaller and f(x) gets larger. Thus, f has an absolute minimum of 0.5 at x = 0.
There are no absolute maximum points. This does not violate the Extreme Value theorem because the function is not defined on a closed interval. Since an absolute maximum must occur at a critical point or an endpoint, and x = 0 is the only such point, there cannot be an absolute maximum.
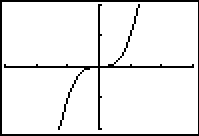
A function's extreme points must occur at critical points or endpoints, however not every critical point or endpoint is an extreme point. The following graphs of y = x3 and
|
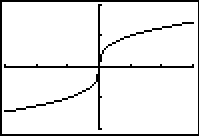
|
| y = x3 in a [-3, 3 1] x [-2, 2, 1] window |
|
Notice that the derivative of y = x3 is y' = 3x2 and the derivative of y = x1/3 is
![]() .
.
The first derivative of y = x3 is zero when x = 0 and the first derivative of y = x1/3 does not exist at x = 0. Although x = 0 is a critical point of both functions, neither has an extreme value there.
In addition to finding critical points using calculus techniques, viewing the graph of a function should help identify extreme values.
In these two examples, note that the first derivative is positive on both sides of x = 0. In lesson 13.2 we will use the First Derivative Test, where the sign of the derivative on either side of a critical point is used to determine whether the critical point is a local maximum, a local minimum, or neither.
