Recursion

This activity extends the “Teaching Foundations of Computer Science With Python on TI-Nspire™ Technology” workshop to study additional topics from computer science with the support of the TI-Nspire™ CX II graphing calculator with Python coding technology. We will explore recursion, a form of iteration that includes repeated, nested calls of a function.

In this activity, we will:

• Define a function using explicit notation
• Define a function using recursive notation
• Use return to send values to another function

Materials for learning

Work along with this blog post by downloading the following materials:

Unit 5, Activity 1: Recursion Recursion notes page

Also, you’ll want to have the following handy:

• TI-Nspire™ CX II graphing calculator (with updated OS)

Unit 5, Activity 1: Recursion

A great introduction to recursion can be found in Unit 5 Activity 1: Recursion. Start by working through that activity, then read through the following discussion of main ideas from the activity.

Explicit notation

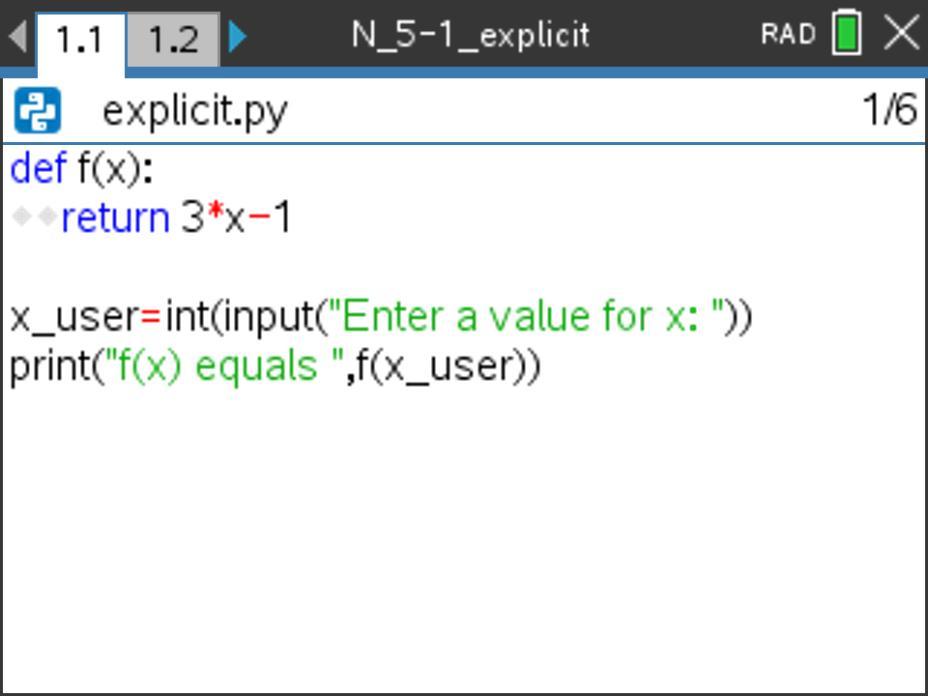
How does the line of code print(“f(x) equals ”,f(x_user)) work?

This print statement prints the text “f(x) equals” then calls the function f(x) and passes the value of the variable x_user into f(x). The function f() returns the value of f(x_user) to the print statement, which then displays it after the “f(x) equals” text.

For example, if the user enters an input of 3, then x_user would have a value of 3 stored to it. The print statement would print f(x) equals and then would call f(x) and send the value of x_user into the f(x) function. Within f(x), the program would multiply the x-value of 3 times 3 then subtract 1. The program would return the value 3*3 – 1 = 9 -1 = 8 to the print statement, resulting in a printed output of f(x) equals 8.

Recursive notation

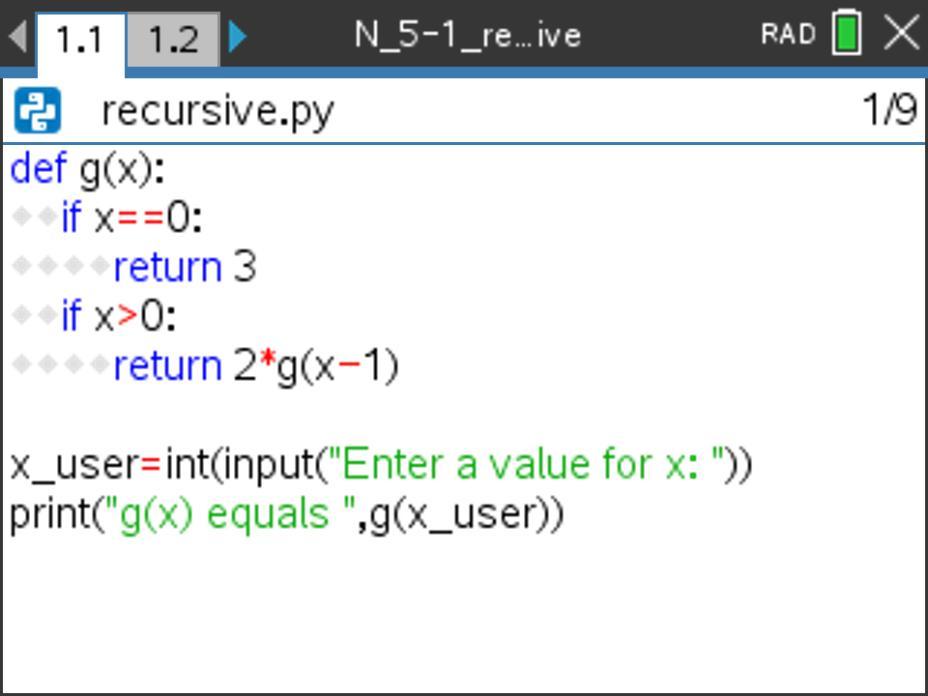
How would the program g(x) evaluate g(3)? Explain this aloud to yourself or a colleague first, then read on for a possible explanation.

When g(3) is called, the value of 3 is passed into the program g(x) for x. Since 3 > 0, the program returns 2*g(2) for g(3). (Do you see why?)

This results in a method call for g(2). The program then runs g(2), which returns as 2*g(1).

This results in a method call for g(1). The program then runs g(1), which returns 2*g(0).

This results in a method call for g(0). The program then runs g(0), which returns 3 since x = 0. (Do you see why?)

Here what has happened so far:

g(3) = 2*g(2)
But what is g(2)?

g(2) = 2*g(1)
But what is g(1)?

g(1) = 2*g(0)
But what is g(0)?

g(0) = 3
Okay, great!

So, what happens next? Does g(3) return 3? No, because that is the value of g(0), not g(3).

However, we can use the value of g(0) to find the value of g(1) to find the value of g(2) to (finally!) find the value of g(3). This is recursion.

Here’s what that would look like: So, g(0) = 3, which then feeds into g(1) = 2*g(0) = 2*3 = 6, which then feeds into g(2) = 2*g(1) = 2*6 = 12, when then feeds into g(3) = 2*g(2) = 2*12 = 24. The function then returns g(3) = 24. This is an example of a recursive call in programming.

Tech tip: Return is found in Menu > Built-Ins > Function.

• How could the g(x) function incorporate an if…else… (or if…elif…else…) structure instead of two if statements?
• How could the function effectively respond to invalid entries such as x = -4?

Comparing explicit and recursive notation

Consider the two example functions we explored in Unit 1, Activity 5: Recursion and unpacked above in this blog. How are these methods similar? How are they different?

Both f(x) and g(x) determine a function value for a specific x-value. Also, they both include user input and resulting output.

However, f(x) directly calculates the output value of f(x) for a specific x-value using an explicit function rule. g(x) recursively determines the value of g(x) by first determining the value of g(x-1), then g(x-2), etc., until the function calls arrive at g(0); then, these values are fed back into the previously called g() functions until you arrive back at the g(x) value that was requested.

g(x) defined recursively is less efficient than the explicit function f(x). However, recursion allows us to do some things that we cannot do with explicit rules.

Recursion notes page

Let’s use an interactive notes page to formalize recursion and how it works.

Here are two pictures of the recursion notes page designed to capture our important learnings about recursion. This notes page uses a program f(x) that is different than the one we studied previously in this blog post.

Recursion overview

Here we see a brief overview of what recursion is and what it looks like. Recursion involves a method that calls itself and involves a base case that will eventually stop the cycle of recursive calls. (In our previous discussion g(0) = 3 resulted from running into the base case.)

Because recursion is inefficient and involves multiple, iterative method calls, it is a memory hog.

A recursive function includes at least two cases:

• Recursive Case — Where the function calls itself again but with a different input; this function call should be moving the function closer to the base case. In the example above, this is the else: return x + f(x-2) part of the function.
• Base Case — The terminating situation in a recursive program that does not use recursion to return an answer. In the example above, this is the if x<1: return 2 part of the function.

Predict the output for this recursive function if it is called with a method call of f(5). Then read on to check your prediction.

This part of the interactive notes page showcases one way we can keep track of a method call for a recursive program.

When f(5) is called, an x-value of 5 passes into f(x). This activates the else command (since 5 is not less than 1), which returns x + f(x-2), which in this case is 5 + f(3).

But what is f(3)? This involves a method call of f(3), which again returns x + f(x-2) since 3 is not less than 1. Specifically, this is returned as 3 + f(1).

But what is f(1)? (Can you feel how we’re in the recursive call part of the program?) A method call of f(1) also returns x + f(x-2) since 1 is not less than 1. Specifically, this is returned as 1 + f(-1).

But what is f(-1)? (Up until this point, we’ve been in the recursive call, but can you see the light of the base case?) A method call of f(-1) returns 2 — wahoo! No more recursive calls! We’ve reached the base case.

Our combined notations so far might look like this:

f(5) = 5 + f(3)

f(3) = 3 + f(1)

f(1) = 1 + f(-1)

f(-1) = 2

Don’t forget, though, that we’re not done! f(5) doesn’t return a value of 2; f(-1) does. We need to plug this value of f(-1) into f(1) so we can plug that into f(3) so we can plug that into f(5). Phew! Doing that produces f(5) = 11 as shown in the image above.

Code this program into your TI-Nspire^TM CX II graphing calculator, and evaluate f(5) using your program. Does it match our work above?

Recursion examples

Here are three additional recursion examples to practice our recursion tracking skills. Explain your thinking aloud as you track your recursive progress on paper.

Use words such as recursive case, base case, and method call in your explanation. Work through these three examples on paper, then enter each recursive function into your TI-Nspire™ CX II graphing calculator to check your answers.

What value will be returned by the method call f(16) for the function f(x) shown below?

What value will be returned by the method call f(2) for the function f(x) shown below?

What value will be returned by the method call f(5,20) for the function f(x,y) shown below?

This program is a nice extension of the recursion topics we’ve explored here. Now there are two formal parameters x and y in the method header. No problem! Take your time and track through this recursion example on paper before testing it in your calculator.

Reflecting on recursion

In this activity, we explored recursion, a form of iteration that includes repeated, nested calls of a function.

Consider:

• Recursion is a form of iteration. How does recursion compare to the other forms of iteration we have studied so far (namely, For loops, While loops, and Do While loops)?

The next activity in this series will explore programming using lists (or arrays).

This series includes:

Do While Loops Counters, Accumulators, and Comparing Loop Types Recursion Programming With Lists Operating on Lists