How Many Solutions to the System?
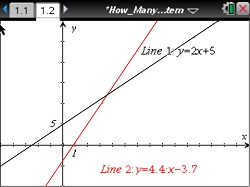
How Many Solutions to the System?
Understand the difference between systems that have one, infinitely many , or no solution.
- Students will understand that a system of two linear equations in two variables can have one solution, no solution, or infinitely many solutions.
- Students will understand the connection between the slopes of the lines and the number of solutions to a system of linear equations in two variables.
- system of two linear equations
- solution
This lesson involves graphing systems of linear equations. The emphasis is on helping students understand the difference between systems that have one, infinitely many, or no solutions. As a result, students will:
- Manipulate a movable line in the coordinate plane in relation to a fixed line to satisfy certain conditions.
- Observe the slope and y-intercept changing as they manipulate the line.
- Discover what must be true for a system of equations to have one, infinitely many, or no solutions.
Vernier EasyData,Vernier EasyLink and Vernier EasyTemp are registered trademarks of Vernier Science Education.

