This lesson involves investigating the relationship between the standard deviation of a population, the area of a set of rectangles, and the standard deviation of the sampling distribution of sample mean areas of the rectangles.

• Students will recognize that samples have smaller variability than the population.
• Students will recognize that the variability in samples is a function of sample size, n, and that the standard deviation of the distribution of sample means is the sample standard deviation divided by the square root of n when the sampling is done with replacement.

• mean
• sample
• sample distribution of sample means
• standard deviation
• standard error
• variance

This lesson involves investigating the relationship between the standard deviation of a population, the area of a set of rectangles, and the standard deviation of the sampling distribution of sample mean areas of the rectangles.
As a result, students will:

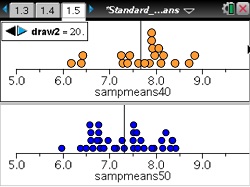
• Simulate a sampling distribution of sample mean areas for samples of size 50 and note the mean and spread.
• Generate a simulated sampling distribution of mean areas for samples of size 40 and compare it to the distribution for samples of size 50.
• Use arrows to produce a series of simulated sampling distributions of sample mean areas for different sample sizes and make a conjecture about the possible relationship between the sample size and the standard deviation.
• Observe the graph of the two variables (sample size and standard deviation of simulated sampling distribution of sample means) and model the relationship with a function, reflecting on why the function makes sense.