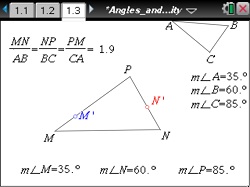
Experiment with the measures of the angles of similar triangles to determine conditions necessary for two triangles to be similar.

• Students will be able to prove that when two pairs of corresponding angles of two triangles are congruent, the third pair of angles will be congruent.
• Students will recognize and apply the Angle-Angle Similarity Theorem.

• proportional
• similarity
• congruence
• corresponding parts

This lesson involves investigating the relationship among angles in similar triangles. As a result students will:

• Change the angle measures of one triangle to match the angle measures in another triangle.
• Prove that when two pairs of corresponding angles of two triangles are congruent, the third pair of angles will be congruent.
• See the equal ratios of the sides when two angle measures match showing that the congruence of two pairs of corresponding angles is sufficient to make two similar triangles.
• Apply the ratio of the sides of similar triangles to find the measure of one side when they know the measure of a given corresponding side.