TI-89 Titanium Graphing Calculator Lesson
Module 16: The Fundamental Theorem of Calculus

Lesson 16.1: Area Functions, A Symbolic Approach

In this lesson you will find functions that represent area under a curve using a symbolic approach. You will be asked to find specific area functions by using the programs rrs and lrs, which were developed in Module 15. You will extend your finding to find the relationship between an area function and its corresponding curve function.

In the previous module you found the area of the region bounded by the graph of f(x) = x², the vertical line x = 1, and the x-axis by using Riemann sums.

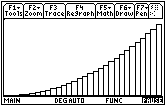
As a review, the procedures and TI-89 functions used to find approximate and exact areas are listed below.

The function r r s was used to approximate the area of the region under the graph of f(x) and above the x-axis betweenx = a and x = b.

Notice that we have factored the constant w from the sum of terms. The exact area under the curve was found by taking the limit of rrs as the number of rectangles approached infinity.

Finding Area

Find the area under the curve f(x) = x² between x = 0 and x = 2.

• Execute NewProb
• Define f(x) = x²
• Take the limit of the function rrs to find the exact area under the curve between x = 0 and x = 2

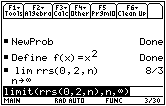
The exact area under f(x) = x² between x = 0 and x = 2 is square units.

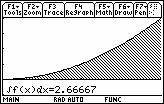
• Illustrate the area by using the 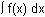function in the Math menu of the Graph screen using a [0, 2] x [-1, 4] window

Finding a Formula for Area

Find the area under the curve f(x) = x² between x = 0 and x = 3 and the area between x = 0 and x = 4.

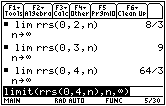
Examine the pattern of the areas as the interval becomes larger.

16.1.1 Predict the area under the curve f(x) = x² between x = 0 and x = 5 then use your calculator to check your prediction. Click here for the answer.

16.1.2 Find an algebraic formula that generalizes the area under the curve f(x) = x² between x = 0 and x = b by evaluating . Click here for the answer.

The area formula is a function of b because it gives the area under the function f(x) = x² between x = 0 and x = b, where b is the quantity that varies. This area function could be described using function notation as .

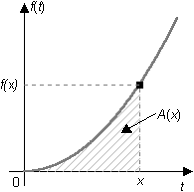
Notice that A and f can both be thought of as functions of the same variable x. The function f evaluated at x yields the y-coordinate of the point (x, f(x)), which lies on the graph of f. The function A evaluated at x yields the area under the graph of f between 0 and the point x on the t-axis. This is illustrated in the diagram below.

Finding Other Area Functions

Riemann sums can be used to find area functions under other curves.

Find the function that gives the area under the curve f(x) = x³ between x = 0 and x = b 0.

• Clear the Home Screen
• Redefine f(x) to be x³
• Find the limit of rrs as n approaches infinity

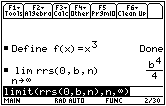
The area function associated with f(x) = x³ is .

Find the area function associated with f(x) = x⁴.

• Define f(x) to be x⁴.
• Find the function for the area between 0 and b

The function for the area under f(x) = x⁴ between 0 and x is

16.1.3 Complete the following table with the curve function whose area function is given.

Area Function
Curve Function

Click here for the answer.

16.1.4 Describe the relationship between the area function A and the curve function f.
Click here for the answer.

The Fundamental Theorem of Calculus

If you noticed that the derivative of the area function is the curve function, you have discovered the Fundamental Theorem of Calculus. The theorem states that the derivative of the area function is the curve function, , and it provides the means to solve a wide variety of real world problems that have no apparent relationship to area under the curve.