Lesson 1
Answer 1
Module 16 - Answers
Lesson 1
16.1.1
By the pattern shown, the area under the curve between x = 0 and x = 5 should be
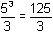, which is confirmed by the TI-89.
, which is confirmed by the TI-89.
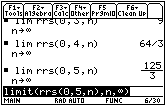
16.1.2
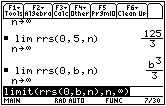
The area under the curve between x = 0 and x = b is given by
.
16.1.3
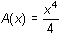
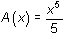
Area Function
Curve Function
f(x) = x2
f(x) = x3
f(x) = x4
16.1.4
The derivative of the area function is the curve function.
Lesson 2
Lesson 2
16.2.1
Evaluate
for each value of x by using the integral key and entering
.
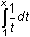for each value of x by using the integral key and entering
.
x
1.0
1.5
2.0
2.5
3.0
3.5
4.0
area
0
0.405
0.693
0.916
1.099
1.253
1.386
16.2.2
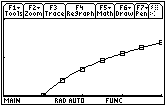
The regression equation is approximately y = ln x
16.2.3
= ln x
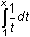= ln x
16.2.4
The derivative of the area function, A(x) = ln x, is
, the curve function.
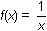, the curve function.
16.2.5
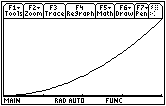
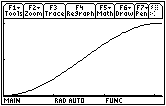
The height of the curve is increasing, so the slopes of the area function are increasing and its graph is concave upward. An approximate area function graph is shown below. The actual values of the area function are not as important as the graph's shape.
Lesson 3
Lesson 3
16.3.1
Predict:
16.3.2
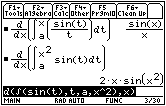
Notice that
appears in the result, 2x sin(x2) .
16.3.3
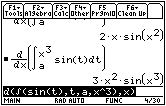
16.3.4
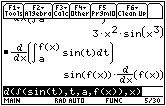
16.3.5
Because
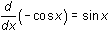
= –(–1) + 1
= 2
Answer 6
16.3.6
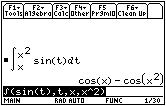
Answer 1
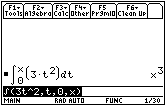
Answer 2
The derivative of the area function with respect to x is f(x).
Answer 3
Answer 4
Answer 5
