Knowledge Base
Solution 32151: Calculating Logistic Growth Using the TI-Nspire™ CAS Family Products.
How do I calculate logistic growth problems using the TI-Nspire CAS family handheld and computer software?
In logistic growth problems, assume that the rate of growth of a population (k) is directly proportional to both the population (y) and the carrying capacity (C) minus the population.
(dy/dt)=ky(C-y)
In this example, eight foxes are introduced into a national park. Assume zoologists have determined a carrying capacity of 250 and a growth rate constant of .001. When will the population reach 100?
Use deSolve( to solve the differential equation. Let x equal time so that you can graph the solution:
1) Open a calculator screen.
2) Press [menu] and choose 4: Calculus.
3) Scroll down to select D: Differential Equation Solver and press [enter].
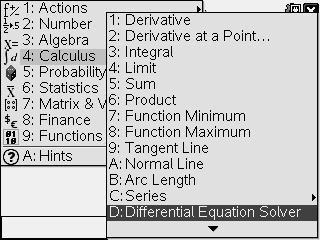
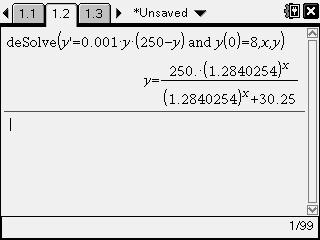
4) Input y'=.001´y´(250-y) and y(0)=8,x,y)
5) Press [enter] and your solution will appear
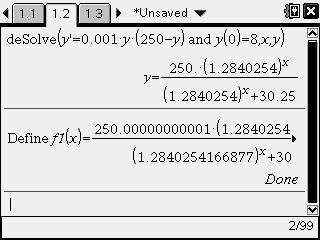
Define f1(x) to be the solution from above:
1) Press [menu] and select 1: Actions>1: Define.
2) Type f1(x)= then copy and paste the solution after the equal sign.
3) Delete y= from expression and press [enter].
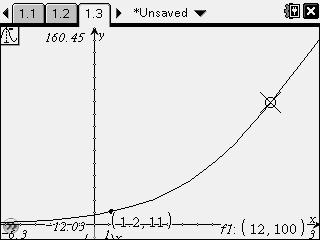
Graph f1(x) and trace the expression until the y-coordinate is about 100:
1) Insert a graphs document by pressing [ctrl] [+page] and selecting. 2: Add Graphs
2) Arrow up and the expression will appear in the f1(x) entry bar.
3) Press [enter] so the expression appears on the graph.
4) Press [menu] and choose 5: Trace>1: Graph Trace.
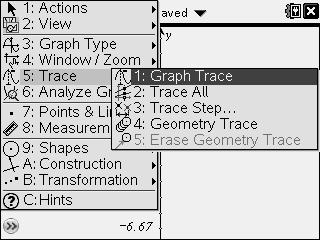
5) Use the right arrow key until the y-coordinate is about 100.
OR:
1) Press [ctrl] [T] to insert a table.
2) Arrow down until the y-coordinate is about 100.
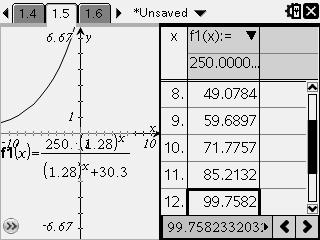
Please Note: The x-coordinate will be the answer for time.
The population will reach 100 in about 12 years.
Please see the TI-Nspire CAS family products guidebooks for additional information.
