Knowledge Base
Solution 21770: Finding the Minimum, Maximum, and Zeros of a Function Using the TI-Nspire™ Family Products.
How do I find the minimum, maximum, and zeros of a function using the TI-Nspire family products?
To find the minimum, maximum, and zeros of a function using a TI-Nspire family product, follow the example listed below. Texas Instruments recommends all TI-Nspire family users update the handheld to the latest operating system. More information on the latest operating system can be found at the TI-Nspire CX and TI-Nspire CX CAS latest software pages.
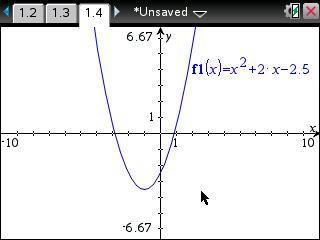
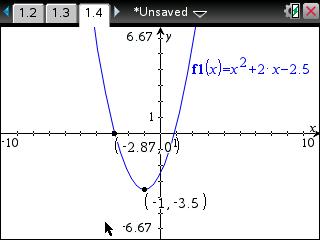
Example function: x^2+2x-2.5
• Press [home] [ctrl] [+page] [2] to insert the Graphs application.
• Press [enter] and the cursor will blink next to f1(x)=, indicating that the handheld is ready for input.
• Input x^2+2x-2.5 and press [enter] to graph the function.
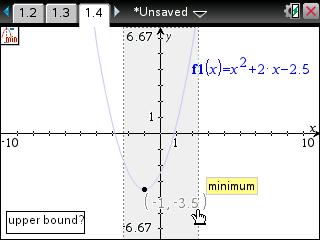
• Since the function's vertex is on the bottom of the graph, the user will be finding the minimum of the function. To access the Minimum tool, press [menu] [6] [2].
• The handheld will prompt for the "lower bound?". Using the arrow keys, move the cursor to the left of the minimum point and press [enter].
• The handheld will prompt for the "upper bound?". Using the arrow keys, move the cursor to the right of the minimum point and press [enter].
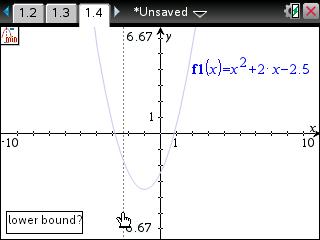
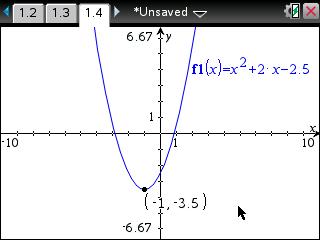
• A "ghost" of the exact coordinate for the minimum point will be displayed. To set the minimum point on the graph, press [enter].
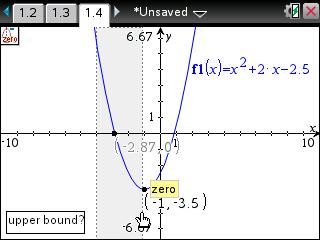
• To find one of the zeros for the example function, press [menu] [6] [1] to access the Zero tool. For this step, the user will be finding the zero on the left-side of the graph.
• The handheld will prompt for the "lower bound?". Using the arrow keys, move the cursor to the left of the zero point and press [enter].
• The handheld will prompt for the "upper bound?". Using the arrow keys, move the cursor to the right of the zero point and press [enter].
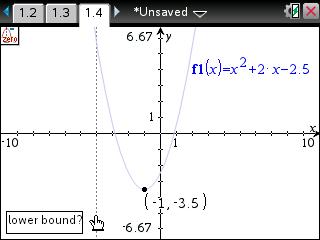
• A "ghost" of the exact coordinate for the zero point will be displayed. To set the zero point on the graph, press [enter]. Repeat the previous (2) steps to find the zero on the right-side of the graph.
Please see the TI-Nspire CX family guidebooks for additional information.