MVT for Derivatives
TI-Nspire™ CX CAS
MVT for Derivatives
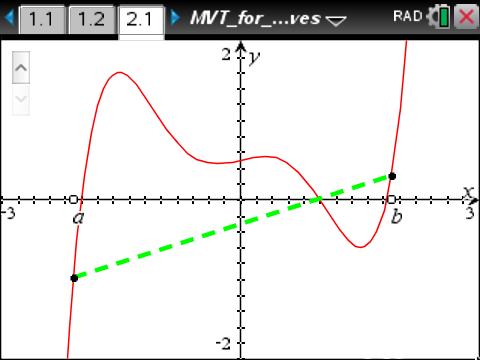
The MVT relates the average rate of change of a function to an instantaneous rate of change.
- Interpret the statement of the Mean Value Theorem in terms of its graphical representation
- Use slopes of secant and tangent lines to explain the relationship between average and instantaneous rates of change demonstrated by the MVT
- Identify functions and/or intervals for which the MVT cannot be applied
- secant line
- tangent line
- average rate of change
- instantaneous rate of change
This lesson uses a graphical representation of the Mean Value Theorem (MVT) to demonstrate how the theorem relates information about the average rate of change of a function to an instantaneous rate of change. As a result, students will:
- Change the endpoints of intervals and relate the changes in the slopes of secant lines to the average rate of change.
- Observe that for the first two functions provided there is always a point in the intervals where the tangent line is parallel to the secant line connecting the endpoints, supporting the conclusion of the MVT.
- Observe a function that is not everywhere differentiable to note when the conclusion of the MVT may not hold.
TI-Nspire™ CX CAS
Vernier EasyData,Vernier EasyLink and Vernier EasyTemp are registered trademarks of Vernier Science Education.

