Activity Overview
In this activity, students explore the real-world problem of a lunar landing and the associated mathematics.
Objectives
Students will:
- choose a coordinate system best suited to the problem
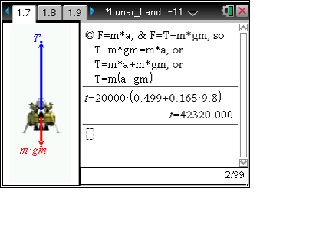
- apply equations of motion and force to solve for unknowns
- determine magnitude and direction of vectors; and
- calculate a spring constant.
About the Lesson
Although it's been done before, landing spacecraft on the lunar surface is not easy. The Moon's gravitational force is 0.165 times the surface gravity on Earth. This difference in surface gravity affects the amount of thrust, or opposing gravitational force, needed to land. Another critical decision for landing on the lunar surface is the landing location. Landing safely means avoiding rocks, holes, or slopes large enough to damage the spacecraft. This is called hazard avoidance. Selecting landing sites that will be advantageous and interesting for science and engineering is also important.
On Apollo missions, the crew looked out the window and visually picked a safe landing location. NASA's latest development projects, with hazard avoidance technology, will enable astronauts to safely land and explore the surface of the Moon. On unpiloted missions, the spacecraft will have systems on board to automatically find the safe areas and land the spacecraft.
Landing safely and learning to live on the Moon or other planetary bodies will give NASA a head start in exploring Mars and other destinations in the solar system.