Numeric, graphical and algebraic solutions to an exponential equation.

• Students will numerically approximate the solution to exponential equations
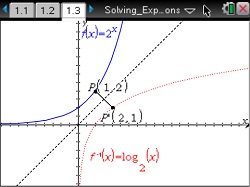
• Students will graphically determine exact solutions to exponential equations using the functions f(x) = a^x and f^-1(x) = log_a(x) and the composition f ° f^-1(x) = x
• Students will find the exact solution to exponential equations using algebraic techniques that employ the relationship.

• Exponential functions and equations
• Logarithmic functions and equations
• Inverse functions
• Composition of functions

This lesson involves numeric, graphical, and algebraic solutions to the equation 2^x = 3. As a result, students will:

• Analyze numeric patterns to predict an approximate solution in a spreadsheet.
• Consider the graphs of both f(x) = 2^x and f^-1(x) = log₂(x) to determine that f(x) = 3 precisely when f^-1(3) = x.
• Use the compositional relationship of 2^log₂(x) = x to solve the equation. That is, the solution to the equation 2x = 3 is x = log₂3, since 2^log₂(3) = 3.
• Consider composition in the opposite order. That is, they will employ the fact that log₂(2^x) = x to solve the equation algebraically.
• Use these techniques to solve similar equations.