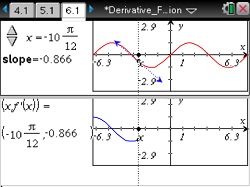
Investigate the symmetric secant line to provide an estimate for the derivative of a function at a point.

• Use the slope of the symmetric secant line to approximate the derivative of a function at a point and generalize properties of functions that affect the accuracy of these estimates
• Explain the relationship between the symmetric difference quotient and the standard difference quotient used to calculate the derivative of a function at a point both graphically and numerically

• secant and tangent line
• difference quotient
• derivative

This lesson provides a visual demonstration of how and when the symmetric secant line can be used to provide a reasonable estimate for the derivative of a function at a point. As a result, students will:

• Explore a variety of function graphs to observe how the slope of the symmetric secant line comes closer to approximating the slope of the tangent line as the value of h decreases.
• Use the symmetric secant line to estimate derivatives at a point and compare these estimates to other numerical and analytic methods.
• Discover the importance of considering the function graph when estimating derivatives by exploring instances in which the symmetric difference quotient provides a value even though the derivative of the function does not exist.