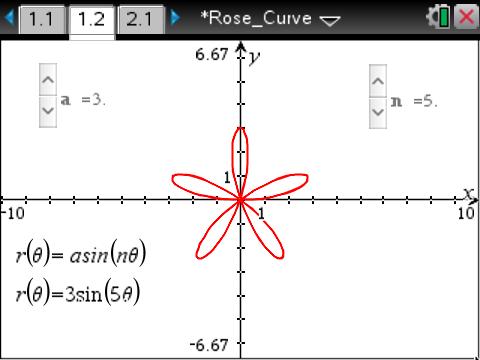
This lesson involves clicking on sliders to observe the effect of changing the values of a and n in the equation r = asin(nθ).

• Students will understand the role of the values of a and n in the equation r = asin(nθ).
• Students will be able to predict the number of petals and their length by examining the polar equation.
• Student will understand the relationship between the equation of a rose curve and the equation of a sinusoidal function.

• amplitude
• frequency
• rose curve
• sinusoidal function

This lesson involves clicking on sliders to observe the effect of changing the values of a and n in the equation r = asin(nθ).

As a result, students will:

• Generalize the roles of a and n in the equation.
• Grab a point and drag it along a sinusoidal function. As the point is dragged, the corresponding polar equation will be formed.
• Compare the equations of the function and the rose curve, and make generalizations about the relationship between the two equations.
• Write equations of rose curves when given information about the petals of the curve.

*Note: This activity contains an optional AP Practice Questions document for those students preparing for the AP Precalculus Exam.