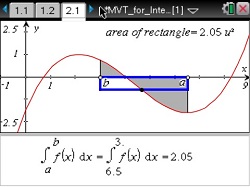
Demonstrate how the average value of a function over an interval is related to the definite integral.

• Describe the statement of the Mean Value Theorem for Integrals in terms of graphical representation
• Describe how the Mean Value Theorem for Integrals relates to the average value of a function
• Explain why the condition of continuity is needed in the hypothesis of the Mean Value Theorem for Integrals to guarantee the existence of a point at which the function attains its average value

• definite integral
• average value of a function

This lesson provides a graphical representation of the Mean Value Theorem for Integrals to demonstrate how the average value of a function over an interval is related to the definite integral. As a result, students will:

• Change the endpoints of intervals to make connections between the definite integral (the area bounded by the graph of f(x) and the x-axis) and a corresponding rectangular area.
• Discover that if a function f(x) is continuous it is always possible to construct a rectangle of height f(c) such that its area is equal to the definite integral and that this value f(c) is the average value of the function over the given interval.
• Use graphical representations of the Mean Value Theorem for Integrals to determine the average value of functions.
• Recognize conditions under which the existence conclusion of the Mean Value Theorem does not hold.