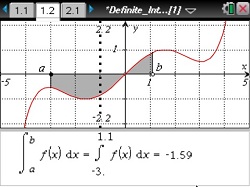
Make visual connections between the definite integral of a function and the signed area between the function and the x-axis.

• Given a graph of a function, determine over what intervals the definite integral of that function will be positive, negative, or zero
• Make generalizations about the behavior of the definite integral of any continuous function.
• Explain the mathematical deficiency in the "area under the curve" description of the definite integral.

• Signed area
• Definite integral
• Continuous function

The intent of this lesson is to help students make visual connections between the definite integral of a function and the signed area between the function and the x-axis. In particular, this lesson provides opportunities to develop a mathematically accurate conception of the definite integral that avoids the "area under the curve" description of the definite integral.