Investigate the mathematics of arc length and sectors.

• Students will recognize that the sum of two central angles that combine to make a circle is 360°.
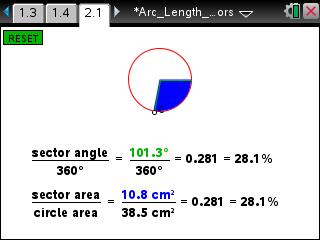
• Students will recognize that the ratio of the central angle to 360° determines the length of an arc.
• Students will recognize that the ratio of the central angle to 360° determines the area of a sector.

• circumference
• area
• arc
• sector angle (or central angle)
• arc measure
• arc length
• sector

This lesson involves dragging a point around a circle to see how arcs and sectors change as the central angle defining them changes. As a result, students will:

• Watch the central angles, sectors, and accompanying ratios change as they drag a point around a circle.
• Specify the percentages (ratios) of circumference and area for various central angles.
• Identify the connection between the central angle and the percentage of circumference and area used to determine arc length and sector area.