绘制微分方程

您可以研究线性和非线性微分方程以及常微分方程组 (ODE)，包括对数模型和 Lotka-Volterra 方程（食者-猎物模型）。 您还可以使用欧拉和龙格-库塔方法的交互实施来绘制斜率和方向字段。

	ODE 输入行： • y1 ODE 标识符 • 表达式 k·y1 定义关系 • 字段 (1,1) 用于指定初始条件 • 用于添加初始条件和设置绘图参数的按钮
	游标用于更改 ODE 系数 k
	斜率场
	通过初始条件的求解曲线

绘制微分方程：

1.

从图形 输入/编辑菜单选择微分 方程。

ODE 将自动分配一个标识符，例如 “y1”。

2.

移动到关系字段并输入定义该关系的表达式。 例如，您可以输入 -y1+0.1*y1*y2。

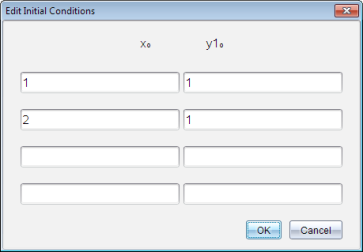
3.

输入独立值 x0 和 y10 作为初始条件。

注： x0 值对问题中的所有 ODE 通用，但只能在第一个 ODE 中输入或修改。

4.

如果您想要研究当前 ODE 的多个初始条件，请单击“添加初始条件”，然后输入条件。

5.

轻按“编辑参数” 设置绘图参数。 选择一种数值解法，然后设置任意其他参数。 您可以随时更改这些参数。

6.

单击确定。

7.

要输入其他 ODE，按下箭头显示下一个 ODE 编辑字段。

在您沿定义的 ODE 移动时，图形会随着更改而更新。 针对为每个显示的 ODE（通过复选框选中）指定的每个 IC，系统将会绘制一个 ODE 解。

微分方程设置摘要

 

解决方案	选择欧拉或龙格-库塔作为数值求解方法。
图表步长间的迭代	仅限欧拉求解方法的计算精度。 必须为  >0 的整数值。 要还原默认值，请选择下箭头并选择默认值。
容差	仅限龙格-库塔求解方法的计算精度。 必须为浮点值  |1×10-14。 要还原默认值，请选择下箭头并选择默认值。
字段	无 - 没有绘制任何字段。 可用于任何数量的 ODE，但如果有三个或以上的一阶 ODE 被激活时则为必需值。 绘制一个或多个 ODE 的解和/或值组合（根据用户配置的坐标轴设置）。 斜率 - 绘制表示一个一阶 ODE 解族的字段。 必须激活恰好一个 ODE。 将坐标轴设置为默认值 （x 和 y）。 将水平轴设置为 x（自变量）。 将垂直轴设置为 y（ODE 的解）。 方向 - 在相平面中绘制表示两个一阶- ODE 方程组解和/或值之间关系的字段（如自定义坐标轴设置所指定）。 必须激活恰好两个 ODE。
坐标轴	默认值（x 和 y）- 在 x 轴上绘制 x 并在 y 轴上绘制 y（活动微分方程的解）。 自定义 - 可让您分别选择要在 x 和 y 轴上绘制的值。 有效输入包括： • x（自变量） • y1、y2 以及 ODE 编辑器中定义的任何标识符 • y1’、y2’ 以及 ODE 编辑器中定义的任何导数
绘图起点	设置求解绘图起始位置的自变量值。
绘图终点	设置求解绘图停止位置的自变量值。
绘图步进	设置绘制值使用的自变量增量。
字段分辨率	设置用于绘制斜率或方向的字段呈现元素（线段）的列数。 仅当字段 = 方向或斜率时才能更改此参数。
方向场: x =	设置绘制非自主方程（引用 x 的方程）时绘制方向字段的自变量值。 绘制自主方程时忽略。 仅当字段 = 方向时才能更改此参数。