Représentation graphique de relations

La représentation graphique de relations est disponible sur la page Graphiques et dans la zone analytique des pages Géométrie.

Vous pouvez définir des relations à l’aide de ≤, <, =, > ou ≥. L’opérateur d’inégalité (≠) n’est pas pris en charge par la représentation graphique de relation.

Type de relation	Exemples
Équations et inégalités équivalentes à y = f(x)	• y = sqrt(x) • y-sqrt(x) = 1/2 • -2*y-sqrt(x) = 1/2 • y-sqrt(x) ≥ 1/2 • -2*y-sqrt(x) ≥ 1/2
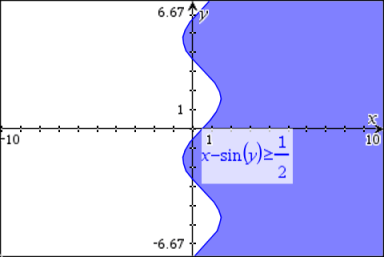
Équations et inégalités équivalentes à x = g(y)	• x = sin(y) • x-sin(y) = 1/2 • x-sin(y) ≥ 1/2
équations et inégalités polynomiales	• x^2+y^2 = 5 • x^2-y^2 ≥ 1/2+y • x3+y3-6*x*y=0
Les relations décrites ci-dessus sont valables dans des domaines limités par des rectangles	• y=sin(x) et -2π<x≤2π • y≤x2|y≥-2 et 0≤x≤3 • {x2+y2≤3, y≥0 et x≤0

Remarque : les restrictions imposées par la session Verrouillage examen peuvent jouer sur les types de relation qu’il est possible de représenter graphiquement.

Pour représenter graphiquement une relation :

1.

Dans le menu Entrée/Modification graphique, sélectionnezRelation.

2.

Saisissez une expression pour la relation.

3.

Appuyez sur Entrée pour représenter graphiquement la relation.

Conseils pour la représentation graphique de relations

▶

Il est facile de définir une relation à partir de la ligne de saisie de fonction. Placez le curseur juste à droite du signe =, puis appuyez sur la touche Espace arrière. Un petit menu s’affiche ; il contient les opérateurs de relation et une option Relation. Une sélection dans le menu a pour effet de positionner le curseur dans la ligne de saisie Relation.

▶

Vous pouvez taper une relation sous forme de texte dans la page Graphiques, puis faire glisser l’objet texte sur l’un des axes. La relation est alors représentée et ajoutée à l’historique des relations.

Avertissement et message d’erreur

Condition d'erreur	Informations supplémentaires
Relation non prise en charge	Relation non prise en charge Remarque : Les relations suivantes sont prises en charge : • Les relations qui utilisent ≤, <, =, >, ou ≥. • Relations polynomiales en x et y • Relations équivalentes à y=f(x) ou x=g(y) et inégalités correspondantes • Les relations décrites ci-dessus sont valables dans des domaines limités par des rectangles
Restrictions de domaines non prises en charge pour certaines classes de relations équivalentes à y=f(x) ou x=g(y) et inégalités correspondantes.	• Les relations équivalentes à y=f(x) et les inégalités correspondantes ne peuvent avoir des contraintes que pour x • Par exemple : y=√(x) et 0≤x≤1 fonctionne, mais pas y=√(x) et 0≤y≤1 • Les relations équivalentes à x=g(y) et les inégalités correspondantes ne peuvent avoir des contraintes que pour x • Par exemple : x=sin(y)|−1≤y≤1 fonctionne, mais pas x=sin(y)|−1≤x≤1