Vous pouvez étudier des équations différentielles linéaires et non linéaires, ainsi que des systèmes d’équations différentielles ordinaires, y compris des modèles de régression logistique et des équations de Lotka-Volterra (modèles proie-prédateur). Vous avez également la possibilité de tracer des champs de tangentes ou de direction en utilisant les implémentations interactives des méthodes d’Euler et de Runge-Kutta.
|
|
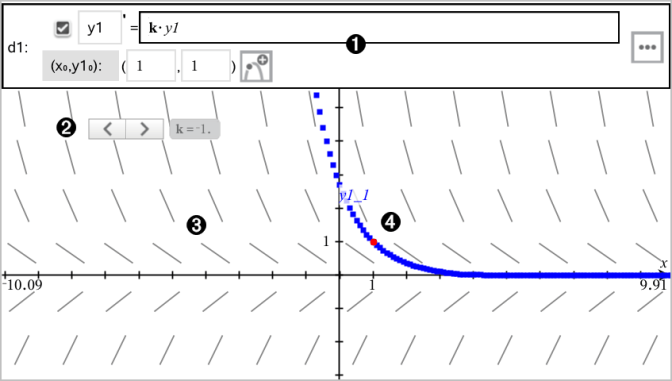
Ligne de saisie d’équation différentielle :
|
||||||||||||
|
|
Curseur pour modifier le coefficient k de l’équation différentielle ordinaire |
||||||||||||
|
|
Champ des tangentes |
||||||||||||
|
|
Une courbe intégrale passant par la condition initiale |
Pour représenter graphiquement une équation différentielle :
| 1. | Dans le menu Saisie/Édition graphique, sélectionnez Équation différentielle. |
Un identificateur, tel que "y1" est automatiquement associé à l’équation différentielle.
| 2. | Accédez au champ de la relation et saisissez l’expression qui définit celle-ci. Par exemple, vous pouvez saisir -y1+0,1*y1*y2. |
| 3. | Saisissez la condition initiale pour la valeur indépendante x0 et pour y10. |
Remarque : Les valeurs de x0 sont communes à toutes les équations différentielles dans une activité, et ne peuvent être saisies ou modifiées que dans la première équation différentielle.
| 4. | (Facultatif) Pour appliquer plusieurs conditions initiales à l’équation différentielle ordinaire, cliquez sur Ajouter des conditions initiales  et saisissez les conditions. |
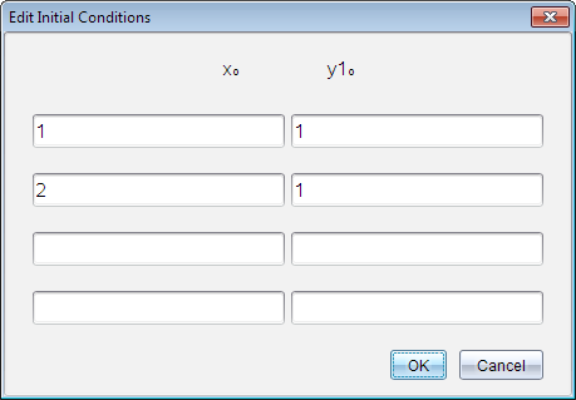
| 5. | Appuyez sur Modifier les paramètres  pour définir les paramètres du tracé. Sélectionnez une Méthode de résolution numérique, puis définissez les paramètres supplémentaires. Vous pouvez modifier ces paramètres à tout moment. |
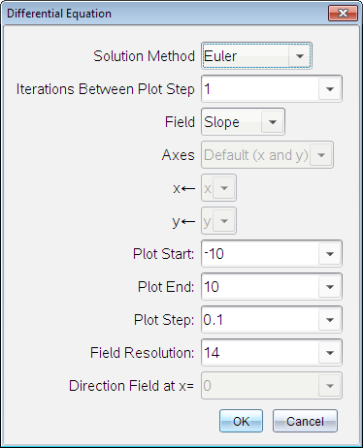
| 6. | Cliquez sur OK. |
| 7. | Pour saisir d’autres équations différentielles, appuyez sur la flèche vers le bas afin d’afficher le champ d’édition de l’équation différentielle suivante. |
Lorsque vous déplacez le curseur sur les équations différentielles ordinaires définies, le graphique se met à jour pour refléter les modifications. Une solution de l’équation différentielle est représentée pour chaque condition initiale spécifiée pour chacune des équations différentielles (dont la case correspondante est cochée).
Récapitulatif des paramètres d’équation différentielle
|
Méthode de Résol |
Sélectionne la méthode de résolution numérique : Euler ou Runge-Kutta. |
|||||||||
|
Nombre d’itérations entre les pas de tracé |
Précision de calcul pour la méthode d’Euler uniquement. Il doit s’agir d’un nombre entier >0. Pour rétablir la valeur par défaut, sélectionnez la flèche vers le bas, puis Valeur par défaut. |
|||||||||
|
Tolérance d’erreur |
Précision de calcul pour la méthode de Runge-Kutta uniquement. Il doit s’agir d’une valeur à virgule flottante |1×10-14. Pour rétablir la valeur par défaut, sélectionnez la flèche vers le bas, puis Valeur par défaut. |
|||||||||
|
Champ |
Aucun : aucun champ n’est tracé. Paramètre disponible quel que soit le nombre d’équations différentielles, mais obligatoire si trois équations du premier ordre ou plus sont actives. Représente graphiquement une combinaison de la solution et/ou des valeurs d’une ou plusieurs équations différentielles (en fonction du réglage du paramètre Axes défini par l’utilisateur). Pente : trace un champ représentant la famille des solutions d’une seule équation différentielle du premier ordre. Une seule équation différentielle doit être active. Règle le paramètre Axes sur la Valeur par défaut (x et y). Configure l’axe horizontal comme l’axe des x (variable indépendante). Configure l’axe vertical comme l’axe des y (solution de l’équation différentielle). Direction : représente graphiquement un champ dans le plan de phase indiquant la relation entre une solution et/ou les valeurs d’un système de deux équations différentielles ordinaires du premier ordre (comme spécifié par le paramètre Axespersonnalisés). Deux équations différentielles doivent être actives. |
|||||||||
|
Axes |
Valeur par défaut (x et y) : trace x en abscisse et y (solutions des équations différentielles actives) en ordonnée. Personnalisé : permet de sélectionner les valeurs à tracer sur les axes x et y respectivement. Les entrées valides incluent :
|
|||||||||
|
Début du tracé |
Définit la valeur de la variable indépendante à partir de laquelle le tracé de la solution débute. |
|||||||||
|
Fin du tracé |
Définit la valeur de la variable indépendante à laquelle le tracé de la solution s’arrête. |
|||||||||
|
Pas du tracé |
Définit l’incrément de la variable indépendante auquel les valeurs sont représentées sur le tracé. |
|||||||||
|
Résolution du champ |
Définit le nombre de colonnes du champ utilisé pour le rendu des éléments (segments de droite) et pour le tracé d’un champ de tangentes ou de direction. Le réglage de ce paramètre ne peut être modifié que si Champ = Direction ou Pente. |
|||||||||
|
Champ de direction à x= |
Définit la valeur de la variable indépendante au niveau de laquelle un champ de direction est tracé lors de la représentation graphique d’équations non autonomes (qui font référence à x). Ce paramètre est ignoré lors du tracé d’équations autonomes. Il ne peut être modifié que si Champ = Direction. |