Graph Logarithms
Graph Logarithms
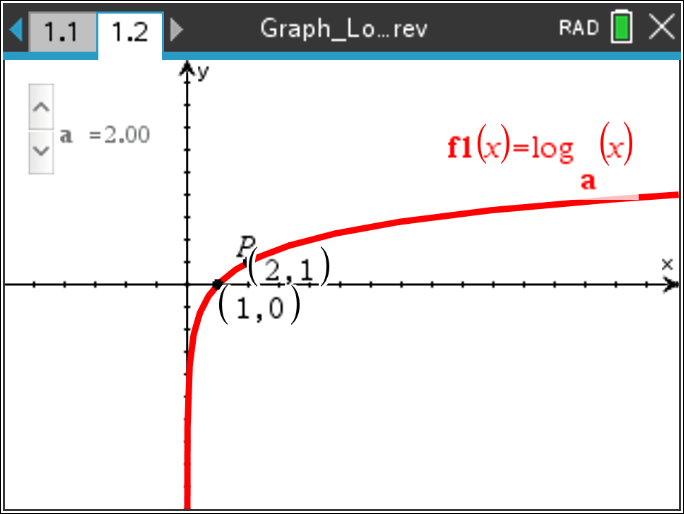
Investigate the graphs of a family of logarithm functions by changing the a-value over the internal 0 to 4.
For the graphs of f(x)=loga(x) where a>0 and a ≠ 1:
- Infer why the conditions a>0 and a ≠ 1 are necessary for the function to be logarithmic.
- Determine that for z>1 the function is increasing and for 0 Determine the x-intercept, y-intercept, domain, range, and asymptotes
- Determine that for a>1 the function approaches infinity as x approaches infinity and that for 0 < a < 1 the function approaches –infinity as x approaches infinity
- logarithm function
- end behavior
- intercepts
- domain and range
- asymptotes
- increasing and decreasing functions
- extraneous solution
Students will investigate the graphs of the family of logarithm functions f(x)=loga(x), by changing the a-value over the interval 0 less than or equal to a less than or equal to 4. As a result, students will:
- Infer why the conditions a>0 and a≠1 are necessary.
- Determine how the value of a affects the increasing or decreasing behavior of the function.
- Determine the x-intercept, domain, range, and asymptotes.
- Describe the end behavior.
NOTE: The time varies for this activity depending on whether students create the TI-Nspire document or use the pre-constructed .tns file.
Vernier EasyData,Vernier EasyLink and Vernier EasyTemp are registered trademarks of Vernier Science Education.

