Activity Overview
The activity is designed to be a lesson in solving absolute value inequalities. The intent is to distinguish the kinds of solutions that absolute value inequalities have and the forms of stating the solutions. More importantly the activity considers two methods of solutions: a graphing method and a transformational method based on graphing. The activity content is divided into 5 problems with multiple pages.
Before the Activity
The student should be able to graph functions and interpret when one function is less than or greater than another from their graphs. Students should be able to navigate through a TI-Nspire lesson: change pages and grab points. This activity could be used with Algebra I students as a guided lesson.
During the Activity
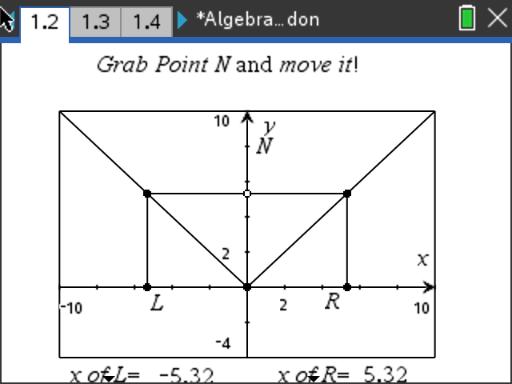
Monitor students working alone or in small groups as they manipulate the graph screens and answer the questions contained in the activity. The question screens reveal the expected responses to the student, but students should endeavor to answer the queries and then compare their responses with those in the activity. The primary goal is to use the graphing solutions to support a transformational method of solving absolute value inequalities contained in Problems 3 and 4. In those problems students are to identify a center and interval around the center described as L and R (values left and right of center) that are used to write solutions.
After the Activity
The activity does not include using <= or >= absolute value inequalities. The inclusion of endpoints in absolute value inequality problems is left to the instructor.