10 Minutos de Código - Python
Explore os princípios básicos de Python com estas instruções curtas e fáceis que incluem tudo o que precisa para começar a programar.
Descarregue um ficheiro Zip com todas as unidades*Estas unidades requerem a tecnologia TI-Nspire CX versão 5.2 ou superior.
Unidade 1: Iniciação à programação em Python
Lição 1: Calcular com Python
Descarregar documentos do professor / alunoNesta primeira lição da unidade 1, iremos aprender como utilizar na aplicação TI-Python as funções matemáticas integradas na calculadora TI-Nspire™ CX II.
Objetivos:
- Utilizar a aplicação TI-Python
- Descobrir as funções matemáticas no Python
- Distinguir o editor de programas do interpretador (shell)
- Utilizar uma instrução de programação no interpretador
Passo 1
A partir do ecrã inicial da calculadora (ou do software), crie um novo documento.
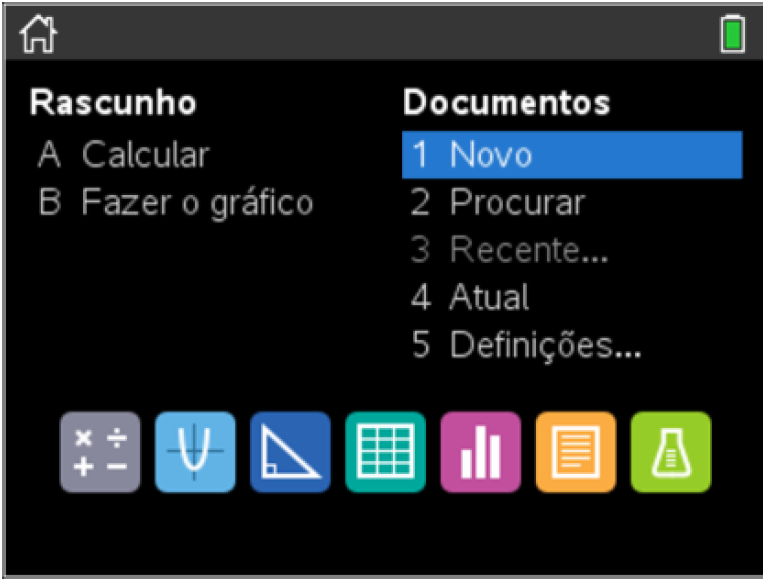
Passo 2
Passo 3
Pode fazê-lo mais rapidamente se pressionar diretamente na tecla ![]() , em vez de deslocar o cursor percorrendo o caminho até à opção pretendida, opção 3: Shell.
, em vez de deslocar o cursor percorrendo o caminho até à opção pretendida, opção 3: Shell.
Passo 4
SUGESTÃO:
A utilização da aplicação Python requer a atualização do sistema operativo para a versão 5.2 ou superior. Os programas desenvolvidos num editor de Python podem também ser diretamente transferidos quando a calculadora estiver conectada a um computador, usando-se um cabo USB.
Clicando na tecla ![]() da calculadora temos acesso a todas as funcionalidades da linguagem Python, presentes nas opções de 1 a 3.
da calculadora temos acesso a todas as funcionalidades da linguagem Python, presentes nas opções de 1 a 3.
Através das opções de 4 a 9 teremos acesso às bibliotecas integradas (Matemática, Aleatório, TI PlotLib…).
Na opção A do ![]() , ou clicando apenas na tecla
, ou clicando apenas na tecla ![]() , tem-se fácil acesso a todas as variáveis criadas no interpretador (modo Shell) ou usada na escrita de um programa em Python.
, tem-se fácil acesso a todas as variáveis criadas no interpretador (modo Shell) ou usada na escrita de um programa em Python.
Passo 5
OBSERVAÇÕES:
O uso da linguagem Python é feito em geral a partir de um programa criado no editor de TI-Python e que é executado no interpretador (Shell). Porém, no interpretador também é possível:
- Efetuar cálculos, definir variáveis integrá-las em cálculos.
- Escrever e executar um programa.
- Executar um programa elaborado no editor de Python e solicitar valores assumidos pelas variáveis do programa.
Passo 6
- Pressionando a tecla
 , depois 1: Ficheiro, seguido de 5: Guardar como… um programa em Python pode ser colocado na pasta PyLib para ser utilizado posteriormente como biblioteca.
, depois 1: Ficheiro, seguido de 5: Guardar como… um programa em Python pode ser colocado na pasta PyLib para ser utilizado posteriormente como biblioteca. - Integrar um programa a partir do menu, tecla
 , opção 1: Ferramentas seguido da opção 7: From PROGRAMA import*…, opção que estará ativa desde que a pasta PyLib não esteja vazia.
, opção 1: Ferramentas seguido da opção 7: From PROGRAMA import*…, opção que estará ativa desde que a pasta PyLib não esteja vazia.
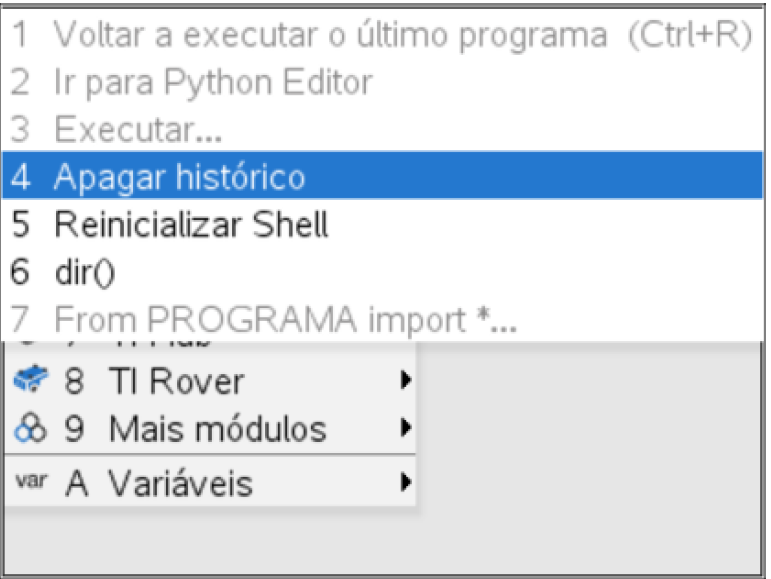
Iniciaremos a nossa exploração da aplicação TI-Python, da TI-Nspire CX II, utilizando o interpretador de Python, também designado por consola ou, ainda, por «Shell».
Passo 7
Alguns comandos básicos.
As variáveis são geralmente designadas utilizando-se letras minúsculas.
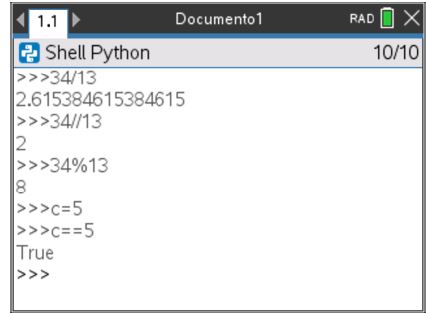
Por exemplo, c ← 5 escreve-se c = 5 em Python e pode ser obtido na calculadora digitando![]() . Esta instrução significa que será atribuído o valor 5 à variável c.
. Esta instrução significa que será atribuído o valor 5 à variável c.
Para testar o valor de c poderemos, por exemplo escrever c == 5 ou
c >= 5 ., e verificar qual o valor lógico da proposição.
Passo 8
Vejamos, agora, como efetuar alguns dos cálculos habituais, por exemplo:
- o resto da divisão de a por b escreve-se a%b
- o quociente euclidiano de a por b obtém-se escrevendo a//b
- x elevado a n escreve-se x**n, também se pode escrever pow(x,n)
- a raiz quadrada de x (x ≥ 0) escreve-se sqrt(x)
- o número π escreve-se pi
NOTA:
A ativação do módulo de Matemática é necessária para efetuar cálculos de raízes quadradas e de frações. Para incorporar este módulo, pressionar tecla ![]() e escolher a opção 4: Matemática e depois 1: from math import* .
e escolher a opção 4: Matemática e depois 1: from math import* .
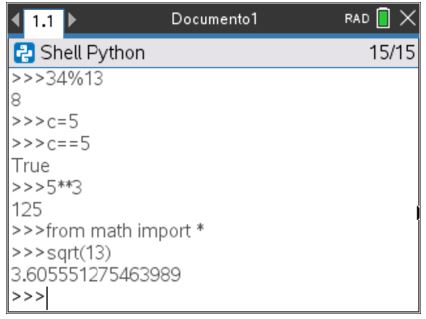
Passo 9
Os comandos relacionados com cadeias de carateres (string)
As cadeias de carateres, string, são definidas colocando o nome entre aspas (duplas “ “ ou simples ‘ ‘), por exemplo, "TI-Python" ou ‘TI-Python’. Algumas funções com cadeias de carateres:
- para obter o tamanho de uma cadeia c usa-se a função len, escrevendo-se len(c) (acessível no menu, tecla
 , na opção 3: Planos integrados e depois 4: Listas).
, na opção 3: Planos integrados e depois 4: Listas). - c[k] retorna o carater de ordem k+1 da string c, de notar que o primeiro carater da cadeia c se obtém fazendo c[0].
- para concatenar duas cadeias de caracteres, basta utilizar o normal operador de adição.
NOTA:
Para apagar as entradas e resultados/mensagens de um interpretador (Shell) deve pressionar-se a tecla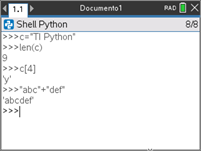
Passo 10
DICA:
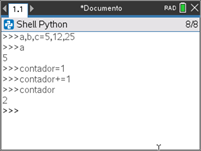
É possível atribuir valores distintos a várias variáveis numa só instrução, para tal atente-se no exemplo do ecrã ao lado.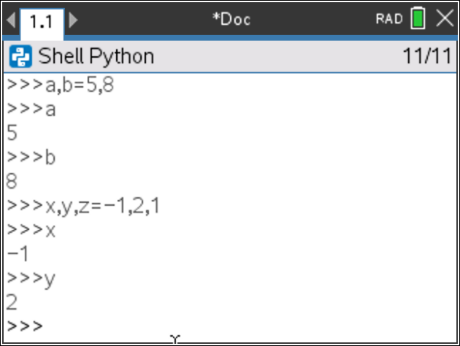
Passo 11
Utilizar uma instrução de programação no interpretador (Shell).
A linguagem Python tem a vantagem de qualquer funcionalidade se poder utilizar e observar independentemente de se criar um programa, isto é, executá-la diretamente no interpretador.
Por exemplo, no ecrã à direita, podemos observar o funcionamento de um ciclo for que se obtém pressionando a tecla ![]() , depois a opção 3 : Planos Integrados e finalmente 2: Controlo, escolhendo-se aqui a opção 4: for index in range(size) : .
, depois a opção 3 : Planos Integrados e finalmente 2: Controlo, escolhendo-se aqui a opção 4: for index in range(size) : .
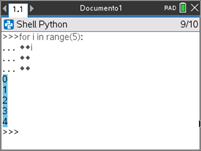
Passo 12
OBSERVAÇÃO:
A utilização direta da escrita com teclado da calculadora também permite que se utilizem as funções em Python, bastando os escrever corretamente. O realce a negrito da designação da função é automaticamente ativado quando as instruções são escritas sem erros e com a sintaxe correta. O software de computador TI-Nspire™ CX também permite a utilização direta do teclado.
Passo 13
APLICAÇÃO DAS APRENDIZAGENS:
Energia Cinética
A energia cinética de um corpo em movimento é dada pela equação EC = 1/2 mv2 em
que:
- m é a massa do corpo em kg.
- v é a velocidade em m/s.
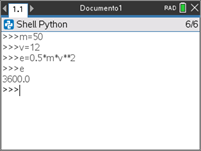
Passo 14
OBSERVAÇÃO:
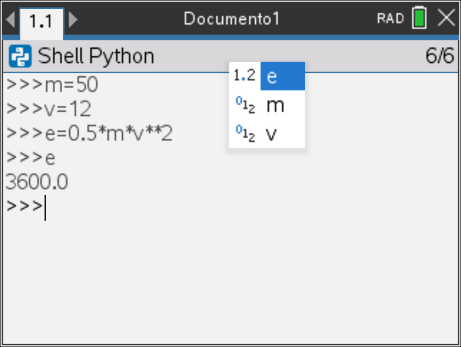
Um programa informático contém instruções que usam variáveis.
Uma variável é um "case" que conserva os dados do programa (números, valores inseridos pelo utilizador, sequências de caracteres, …) armazenando-os na memória do computador. A atribuição de um valor a uma variável é feita utilizando a tecla ![]() que insere no interpretador o sinal = .
que insere no interpretador o sinal = .
Passo 15
O editor de Python permite o acesso a todas as variáveis usadas no respetivo programa, mas também no modo de interpretador se pode aceder a todas as variáveis do último programa executado.
Para tal, basta pressionar a tecla ![]() , escolher a opção A: Variáveis e por fim 2: Variáveis, Todos .
, escolher a opção A: Variáveis e por fim 2: Variáveis, Todos .
Lição 2: Os tipos de dados em Python
Descarregar documentos do professor / alunoNesta segunda lição da Unidade 1, descobrirá como utilizar os tipos de dados em Python.
Objetivos:
- Conhecer os diferentes tipos de dados da linguagem Python.
- Formatar um dado numérico.
Passo 1
Conheça os tipos de dados utilizados.
Ao criar um programa em linguagem Python, pode ser necessário conhecer o tipo de variável que está a ser utilizada, ou até modificá-la para uso posterior. Por exemplo, se uma grandeza dada por um programa em Python corresponde a uma grandeza relativa a uma medida em Física, não é necessariamente apropriado manter um resultado com 6 casas decimais.
Vejamos como criar um programa na aplicação TI-Python para verificar e distinguir os tipos de grandezas utilizadas:
- uma cadeia de caracteres
- um número real
- um número irracional, √2 por exemplo.
Passo 2
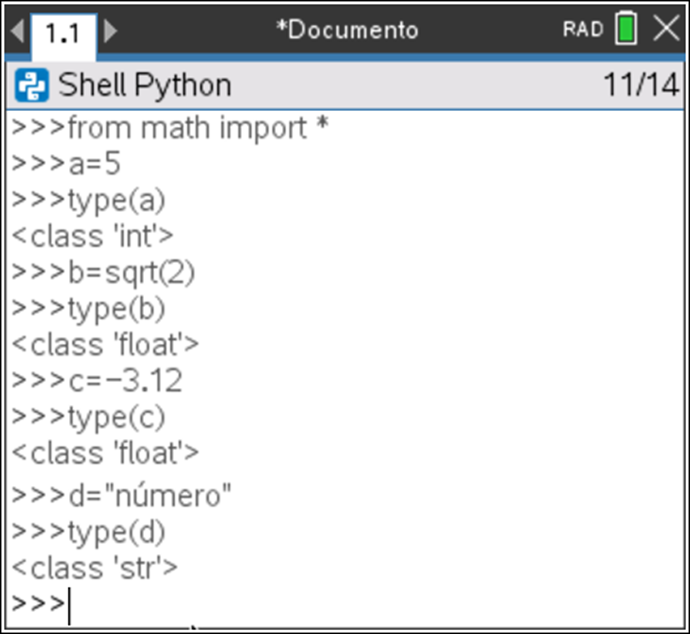
Usando a função type(), poderá obter o tipo de uma dada variável, por exemplo:
- crie um novo documento Python com uma página Shell Python;
- importe o módulo maths (tecla
 , depois opção 4: Matemática e por fim opção 1: from maths import* );
, depois opção 4: Matemática e por fim opção 1: from maths import* ); - defina variáveis, de diferentes tipos, no interpretador;
- utilizando a função type() verifique qual a natureza de cada variável que definiu.
Passo 3
OBSERVAÇÃO:
Todos os comandos usados podem ser introduzidos diretamente com o teclado, escrevendo-os. A função type() para determinar a natureza de uma dada variável é digitado manualmente ou inserido através do menu, opção 3:Planos integrados, depois opção 5: Type e por fim opção 6: type().
DICA:
Ao premir a tecla de direção ![]() seguida de tecla
seguida de tecla ![]() pode copiar uma qualquer linha já executada para a linha de edição.
pode copiar uma qualquer linha já executada para a linha de edição.
Passo 4
NOTAS:
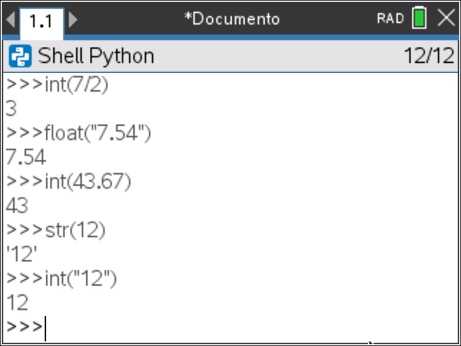
- O operador int() tem como resultado, sempre que possível, o número inteiro representado por uma cadeia de carateres numéricos e a parte inteira de um número compreendido entre - 2 147 483 648 e + 2 147 483 648 (codificação de 32 bits, ou seja 4 bytes)
- O operador str() transforma um número numa cadeia de carateres.
- O operador float() tem como resultado, sempre que possível, o número decimal definido por uma cadeia de carateres.
Passo 5
DICA:
Para incrementar uma variável, dispomos de duas possibilidades:
- Escrever, por exemplo: contador = 0
contador = contador +1
solicitar a exibição da variável contador
1
- Ou então, escrever: contador = 1
definir o incremento contador += 3
contador
4
Passo 6
SUGESTÃO:
Utilize, sempre que útil, os habituais atalhos para copiar, Ctrl + C, colar, Ctrl + V, e cortar, Ctrl + X.
Na edição texto, para apagar um carater introduzido erradamente deve clicar na tecla ![]()
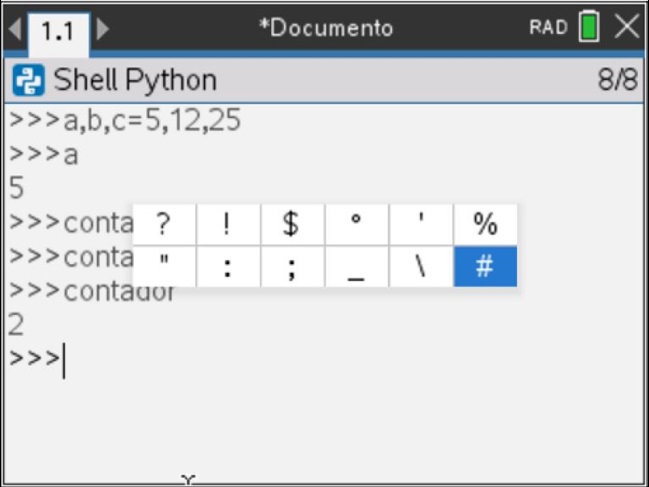
Comentários num programa
Pode inserir comentários nos seus programas em Python, para tal deve colocar o símbolo # no início do comentário, desta forma a respetiva linha não será interpretada no Shell. O símbolo # pode ser obtido clicando na tecla ![]()
Poderá ainda usar o atalho ![]() e
e ![]() para definir uma linha de comando como comentário, o mesmo atalho elimina a referência como sendo um comentário.
para definir uma linha de comando como comentário, o mesmo atalho elimina a referência como sendo um comentário.
Passo 7
MAIS ALÉM:
Formatação de números
O método de formatação em uma string é uma ferramenta muito poderosa que permite criar cadeias de carateres substituindo certos campos (colocados entre chavetas) por valores (atribuídos como argumentos da função de formatação) depois de os converter. Pode-se, ainda, especificar dentro de cada chaveta um código de conversão, bem como a forma de apresentação. Vejamos dar alguns exemplos:
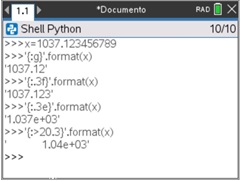
>>> x=1037.123456789
>>> ‘{ :g}’.format(x) # escolha do formato mais apropriado ‘1.04E+03’
>>> ‘{ :.3f}’.format(x) # fixa o número de casas decimais ‘1037.123’
>>> ‘{ :.3e}’.format(x) # notação científica ‘1.037E+03’
>>> ‘{0 :20.3f}’.format(x) # especifica o comprimento da cadeia ‘ 1037.123’
Passo 8
>>> ‘{0 :>20.3f}’.format(x) # para justificar à direita ‘ 1037.123’
>>> ‘{0 :<20.3f}’.format(x) # para justificar à esquerda ‘1037.123 ‘
>>> ‘{0 :^20.3f}’.format(x) # centrado ‘ 1037.123 ‘
>>> ‘{0 :+.3f} ; {1 :+.3f}’.format(x, -x) # exibir sempre o sinal ‘+1037.123 ; -1037.123’
>>> ‘{0 : .3f} ; {1 : .3f}’.format(x, -x) # exibir um espaço se x>0 ‘ 1037.123 ; -1037.123’
A função .format(), aplicada a variáveis numéricas tem a seguinte estrutura base:
‘{[ordem da variável no argumento da função]:[preencher][alinhar][sinal][largura].[precisão][tipo]}’.format(var1,var2,…)
Passo 9
cujos respetivos campos explicitam-se abaixo:
- [ordem da variável no argumento da função] - a função .format() pode ter como argumento várias variáveis, sendo que pode ser precedida por várias estruturas base em que este campo defini qual a variável a que se refere a estrutura;
- [preencher] - um qualquer carater que irá preencher os espaços vazios da cadeia de caracteres;
- [alinhar] - definição do alinhamento, sendo: < esquerda; > direita e ^ centro
- [sinal] - define que, caso do valor numérico seja positivo, se apresenta o sinal + , espaço em branco ou nada;
- [largura] - número de carateres da cadeia, isto é, comprimento da cadeia de carateres, podendo alguns serem espaço vazios (comprimento mínimo da cadeia);
- [precisão] - número de casas decimais dependo do tipo de formatação;
- [tipo] - f → decimal, e → decimal em formato exponencial minúsculo, E → decimal em formato exponencial maiúsculo, g → algarismos significativos, b → Binário (apenas argumentos inteiros).
Lição 3: As funções em Python
Descarregar documentos do professor / alunoNesta terceira lição da Unidade 1, utilizará o editor de programas da aplicação TI-Python para criar funções e, depois, executar o programa e/ou as funções e observar os resultados no interpretador.
Objetivos:
- Descobrir o conceito de função em linguagem Python.
- Construir funções.
Passo 1
Descobrindo o conceito de função em Python.
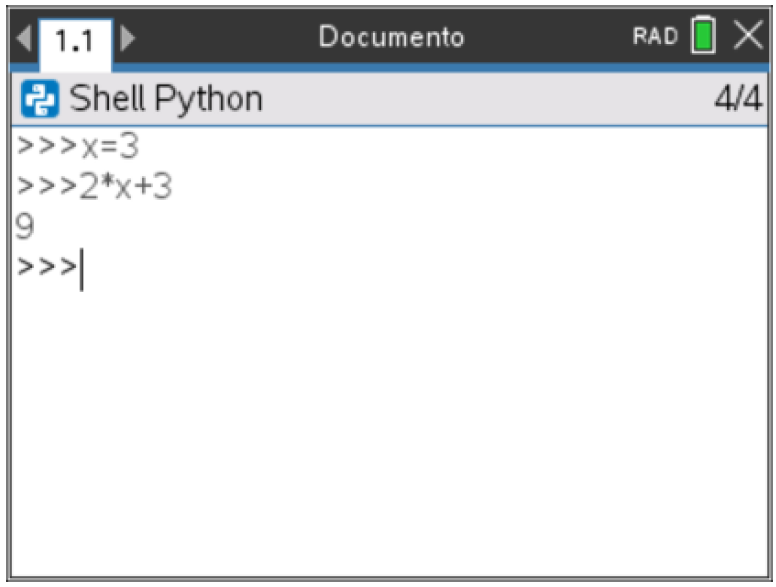
Implementar, no interpretador, o seguinte algoritmo:
x ← 3
y ← 2 × x + 3
É um processo relativamente simples.
Mas se pretender repetir o cálculo para outro valor de x, terá que escrever de novo toda a sequência de instruções. Assim, numa situação menos trivial pode tornar-se muito aborrecido e, com certeza, pouco eficaz. Somos, portanto, levados a criar uma função que nos permita replicar facilmente o processo algorítmico.
Passo 2
Em algoritmia, uma função pode considerar-se como uma sequência de instruções, executando uma determinada tarefa, utilizando um ou mais argumentos (ou até nenhum, em alguns casos).
À função é atribuído um nome, de preferência sugestivo e simples.
- A programação de uma função começa sempre por def seguido pelo nome da função e depois pelos seus argumentos. Esta linha termina com o símbolo :
- Os dois pontos (..) assinalam o início do bloco das instruções que definem a função, sendo que todas as linhas com estas instruções são indentadas, ou seja, deslocadas para a direita em relação à 1ª linha. No início de cada linha, adicionamos o mesmo número de espaços.
- A função retorna um único resultado por intermédio do comando return. O resultado pode ser constituído por uma lista de resultados, uma cadeia de caracteres, …
A correta indentação (recuo) das linhas de instrução, que se pode obter com a tecla de tabulação ou a tecla de espaço ou ainda no menu, é fundamental: qualquer instrução indentada após def() será executada como um bloco. A indentação não deve variar (número de espaços, alternância entre tabulações e espaços. . .) no bloco.

Passo 3
SUGESTÃO:
Uma função permite decompor o problema estudado noutros subproblemas e, assim, evitar a repetição de instruções. Uma vez definida uma função, ela pode ser "chamada" durante a execução do programa tantas vezes quanto as necessárias.
Uma função pode não ter argumentos. Pode também ser "chamada" noutro programa: basta inseri-la numa instrução com os valores dos argumentos.
Passo 4
IMPLEMENTAÇÃO DE UM EXEMPLO:
- Criar um novo programa na aplicação TI-Python
Pressionar a tecla ![]() e escolher no menu a opção A: Adicionar Python, depois escolher 1: Novo. De seguida, na janela que se abre, atribua um nome ao programa.
e escolher no menu a opção A: Adicionar Python, depois escolher 1: Novo. De seguida, na janela que se abre, atribua um nome ao programa.
Para validar o nome do programa pode clicar sobre o botão OK, ou pressionar a tecla ![]()
Passo 5
NOTA:
Por defeito, o editor de programas inicia com uma página em branco (sem incluir bibliotecas). No entanto, a edição pode ser facilitada se conhecer as bibliotecas necessárias para criar um novo projeto.
- O nome do programa surge na barra inicial da página de edição com a extensão .py.
- Pressionar a tecla
 para abrir a lista de submenus do editor.
para abrir a lista de submenus do editor.
Passo 6
- As instruções específicas da linguagem Python estão no menu 4: Planos integrados e contém todas as instruções necessárias para escrever um programa, que são:
1: Definição de funções
2: Ciclos e condições
3: Operadores Relacionais e Lógicos
4: Listas
5: Tipos de dados
6: Entradas e saídas de dados
- Selecionar a instrução para construção de uma função no editor, selecionando a opção 1: Funções, dos planos integrados, seguida da opção 1: def function():
Passo 7
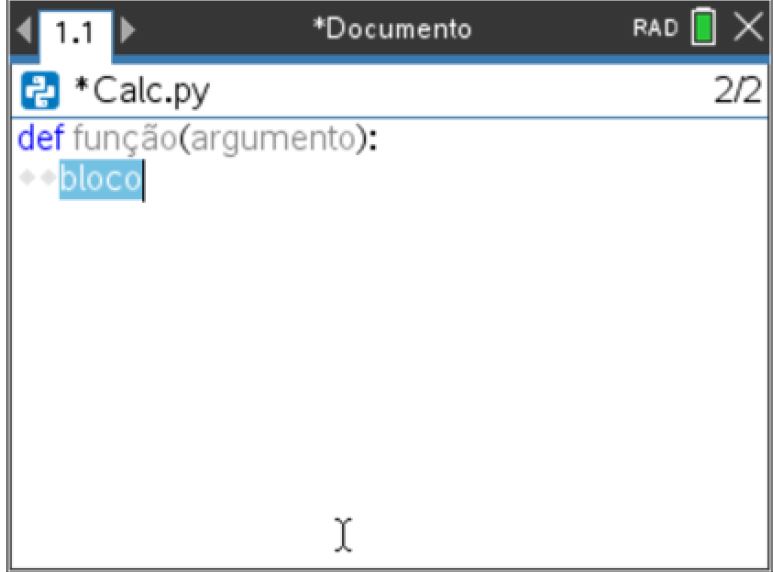
- Observar a ação realizada pela calculadora, isto é, a exibição automática da estrutura de uma função em Python.
- Os campos de preenchimento surgem com texto acinzentado, podendo ser facilmente preenchidos usando a tecla
 da calculadora para se deslocar de campo para campo.
da calculadora para se deslocar de campo para campo. - Quando o cursor estiver num campo que pode ser preenchido, o texto passa a estar sombreado a azul claro.
- Para definir a função f que permita implementar o algoritmo escrito no passo 1, deverá obter o ecrã ao lado. Observará a indentação automática do cursor.
Passo 8
- Continuar de seguida com as instruções para implementação do algoritmo. Recordar que a atribuição de um valor a uma variável é realizada com o símbolo = .
- Pressionar a tecla
 , depois selecionar 4: Planos integrados, de seguida 1: Funções e finalmente 2: return, para completar o pequeno programa com a instrução de saída da imagem pela função.
, depois selecionar 4: Planos integrados, de seguida 1: Funções e finalmente 2: return, para completar o pequeno programa com a instrução de saída da imagem pela função. - Pode também digitar a instrução manualmente, usando o teclado alfanumérico da calculadora, ficando destacada logo que seja reconhecida.
Passo 9
Agora está pronto a executar o seu programa.
- Pressionar
 , atalho para executar um programa.
, atalho para executar um programa. - O interpretador é exibido e surge uma mensagem a dar conta do carregamento do programa
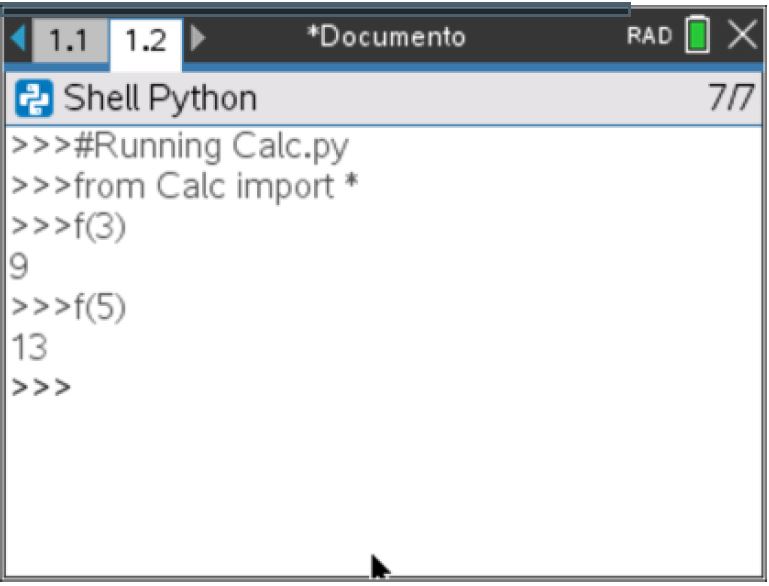
- Preencher a linha de comando com o nome da função e os argumentos, neste caso apenas um, e valide, pressionando a tecla

- Utilizar a deslocação do cursor para cima,
 , para selecionar um comando anterior e de seguida clicar na tecla
, para selecionar um comando anterior e de seguida clicar na tecla  pode a obter na atual linha de comando.
pode a obter na atual linha de comando.
Passo 10
SUGESTÃO:
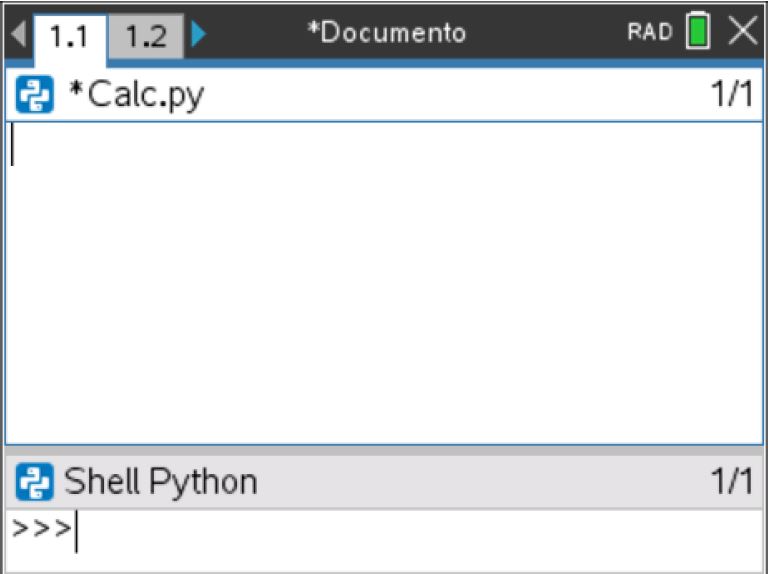
A edição e a execução de um programa em Python, com a TI-Nspire CX, pode ser facilitada se dividir a página em duas aplicações, numa o Editor e noutra o Interpretador. Para tal clicar na tecla ![]() , depois opção 5 : Esquema da página., e selecionar o formato que interessar, adicionando na segunda página o interpretador (Shell) da aplicação TI-Python.
, depois opção 5 : Esquema da página., e selecionar o formato que interessar, adicionando na segunda página o interpretador (Shell) da aplicação TI-Python.
Posteriormente, usando no editor o atalho ![]() o cursor passará automaticamente para a janela do interpretador, que se encontra sob a do editor, e deste modo poderá a executar o programa vendo a edição do mesmo. Poderá separar as duas aplicações da divisão da página usando o atalho
o cursor passará automaticamente para a janela do interpretador, que se encontra sob a do editor, e deste modo poderá a executar o programa vendo a edição do mesmo. Poderá separar as duas aplicações da divisão da página usando o atalho ![]() .
.
Aplicação: Os diferentes tipos de dados em Python
Descarregar documentos do professor / alunoNesta aplicação da Unidade 1, irá construir alguns programas recorrendo aos conhecimentos adquiridos nas lições desta unidade:
- Funções em linguagem Python
- Criação de variáveis numéricas e cadeias de carateres
Objetivos:
- Criar um conversor de sistemas de medida de temperatura.
- Criar um programa que permita desenvolver uma expressão algébrica
Passo 1
EXEMPLO:
Conversor de Temperatura
Para medir a temperatura em Portugal, utilizamos como unidade de medida o grau Celsius (°C). Nos países anglo-saxónicos, utilizam como unidade de medida o grau Fahrenheit (°F).
O desafio para este exemplo consiste em programar uma função que permita converter a temperatura entre estas duas unidades de medida, nos dois sentidos: °C ↔ °F .
Existirá uma temperatura igual nas duas unidades?
Consideremos a função que permite converter a temperatura de graus Celsius para graus Fahrenheit:
t(°F) = 9/5 × t(°C) + 32.
Donde, resulta que podemos utilizar em sentido contrário a função:
t(°F) = t(°C) × 1.8 + 32

Passo 2
IMPLEMENTAÇÃO DO EXEMPLO:
- Abrir a aplicação TI-Python e começar um novo programa.
- Nomear o programa como Temperatura e validar pressionando a tecla

- Abrir na mesma página uma nova aplicação (premir tecla
 seguido de 5: Esquema de página), permitindo obter na primeira aplicação o Editor já aberto e na segunda o Interpretador (Shell).
seguido de 5: Esquema de página), permitindo obter na primeira aplicação o Editor já aberto e na segunda o Interpretador (Shell). - Importar o módulo de Matemática da TI-Nspire CX (premir tecla
 seguido de 5: Matemática… e finalmente 1: from math import *)
seguido de 5: Matemática… e finalmente 1: from math import *) - Criar uma primeira função de conversão no sentido °C → °F (
 seguido de 4: Planos integrados e finalmente 1: funções).
seguido de 4: Planos integrados e finalmente 1: funções). - Utilizar a tecla
 para passar de uma aplicação para a outra (Editor para Interpretador e vice-versa), ou o touchpad colocando o cursor na aplicação pretendida.
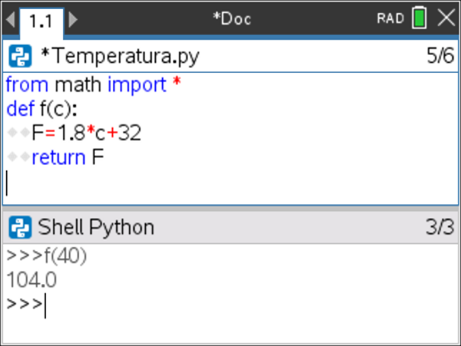
para passar de uma aplicação para a outra (Editor para Interpretador e vice-versa), ou o touchpad colocando o cursor na aplicação pretendida. - Executar o programa (atalho
 ) e utilizar no interpretador a função criada para converter em grau Fahrenheit uma temperatura de 40°C, f(40).
) e utilizar no interpretador a função criada para converter em grau Fahrenheit uma temperatura de 40°C, f(40).
Passo 3
SUGESTÃO:
Ao executar um programa no modo interpretador (Shell)) pode premir a tecla ![]() e selecionar a função, sem argumentos, que pretende utilizar. Para a executar basta inserir os argumentos e pressionar a tecla
e selecionar a função, sem argumentos, que pretende utilizar. Para a executar basta inserir os argumentos e pressionar a tecla ![]() , assim obterá os resultados da mesma.
, assim obterá os resultados da mesma.
- Concluir a construção do programa Temperatura, definindo de forma análoga a função para a conversão contrária: °F → °C.
ATENÇÃO:
Utilizar a opção 2: Retirar indentação do submenu 3: Editar do menu do editor para retornar à linha não recuada (caso contrário, uma mensagem de erro será exibida quando o programa for executado). Pode usar o atalho ![]() .
.
- Resumindo, a função f(c) converte a temperatura de °C para °F e a função c(f) realiza a conversão de °F para °C .
- Guarde o programa (
 ), sendo a sintaxe verificada e se for detetado algum erro, este será assinalado. No fim da gravação será exibida a seguinte mensagem:
), sendo a sintaxe verificada e se for detetado algum erro, este será assinalado. No fim da gravação será exibida a seguinte mensagem:
Passo 4
Para encontrar, finalmente, um valor da temperatura que seja igual nas duas unidades de medida é possível fazê-lo através de diversos métodos implementando ciclos e testes, mas que apenas veremos nas unidades 2 e 3.
Assim, prosseguiremos utilizando um ciclo que permita obter medidas com passos de 10 graus (para possivelmente vir a refinar, criando um outro programa).
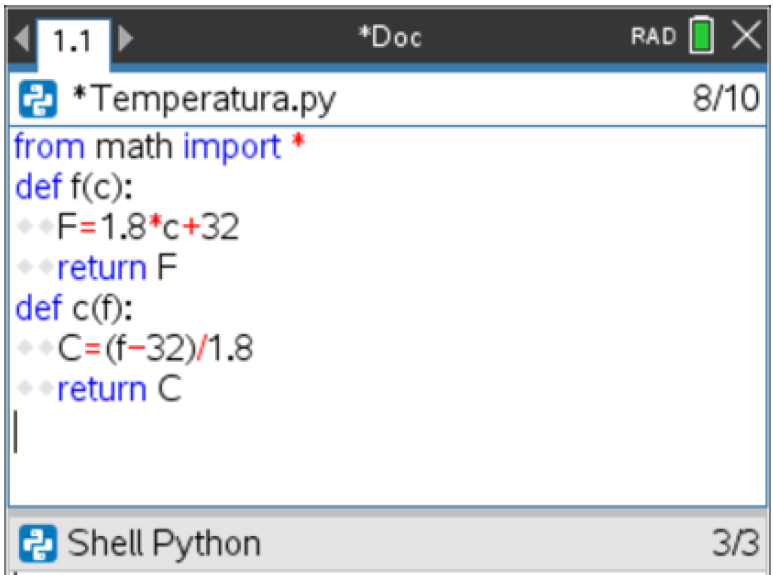
- Pressione a tecla
 , escolha 1: Ações e depois 3: Criar cópia…
, escolha 1: Ações e depois 3: Criar cópia…
- É sugerido nome Temperatura1 para a cópia. Validar ou modificar.
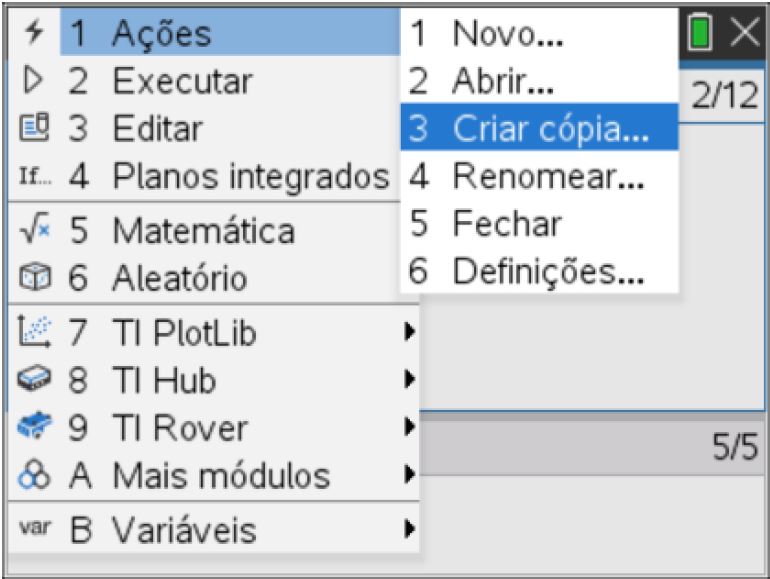
- Deve notar que o programa foi duplicado na página 2 do problema 1, pelo que o número da página será 1.2.
Procuraremos a solução no intervalo [-60; 10] em passos fixados inicialmente de 10 graus. O passo será um argumento da função, portanto a ser inserido pelo utilizador.
Passo 5
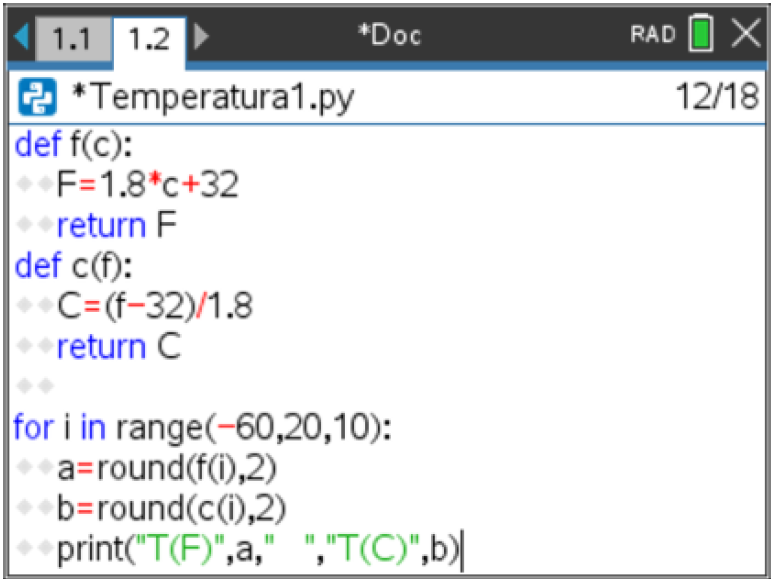
Vamos recorrer a três funções ainda não utilizadas, que são:
- round(a,2) - para arredondar o valor da variável numérica a com 2 casas decimais.
- for i in range(início, fim, passo) - para gerar um conjunto de temperaturas correspondentes, em ambas as unidades.
- e a instrução print() para apresentar os resultados.
Passo 6
Estas funções obtêm-se através do menu, tecla ![]() , e da opção 4: Planos integrados e, respetivamente, das opções:
, e da opção 4: Planos integrados e, respetivamente, das opções:
· 5: Tipo · 2: Controlo · 6: I/O
A tecla ![]() pode facilitar a edição das instruções, pois permite deslocar mais rapidamente entre campos.
pode facilitar a edição das instruções, pois permite deslocar mais rapidamente entre campos.
Deverá obter os resultados corretos depois de executar o programa (![]() ).
).
Desta forma, por observação dos resultados do programa, encontrará a resposta para a questão suscitada!
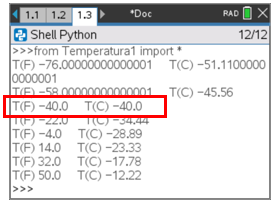
Passo 7
SUGESTÃO:
Para melhorar o programa, pode ser necessário modificá-lo, solicitando ao aluno que proponha o intervalo de variação da temperatura ao iniciar o programa, bem como o valor do passo (incremento para os valores da temperatura).
Portanto, poderá utilizar-se uma função cujos quatro argumentos sejam os valores de início, fim e passo ou, então, instruções que solicitem ao utilizador, um a um, os valores destes parâmetros (por exemplo, passo=float(input(‘Passo=’))).
NOTA:
Tenha cuidado ao executar um ciclo do tipo for i in range(início, fim, passo), pois o ciclo termina com a variável i a tomar o valor de “fim – passo”. O ciclo FOR, será abordado durante o estudo da Unidade 2, na lição 2.- Lição 1
- Lição 2
- Lição 3
- Aplicação
Unidade 2: Iniciação à programação em Python
Lição 1: Funções condicionais
Descarregar documentos do professor / alunoNesta terceira lição da Unidade 2 vamos descobrir como repetir um procedimento ou um conjunto de instruções utilizando um ciclo não limitado WHILE.
- Explorar e implementar o ciclo não limitado WHILE
- Utilizar o ciclo WHILE em exemplos simples
Passo 1

Estrutura de uma função condicional.
Por exemplo, “a = b” ou então “a ≥ b”, ou ainda “n é par”, são exemplos de condições que são verificadas pela concretização das variáveis por alguns valores: as soluções.
Assim, num programa podemos testar uma condição verificando se ela se transforma numa proposição verdadeira ou numa proposição falsa, conforme concretizamos a variável com um certo valor ou um outro qualquer. Designamos este processo por verificação condicional.Passo 2
OBSERVAÇÕES:
- Na linguagem Python não existe nenhuma instrução para indicar o fim da função condicional. É, mais uma vez, a indentação que desloca as instruções condicionais A e B para a direita, definindo assim os blocos de instrução da função condicional.
- Utiliza-se elif como contração de else if .
- Para testar a igualdade entre dois valores, na linguagem Python, utiliza-se a sintaxe “ = = ” (dois sinais de igual seguidos).
Passo 3
EXEMPLO:
Uma empresa de aluguer de veículos apresenta aos seus clientes o seguinte contrato:
Um custo base de 66€ ao que se adiciona
o custo de 0,25€ por cada quilómetro
percorrido a partir dos 70 quilómetros.
Crie um programa que permita calcular automaticamente o custo, C, do aluguer de um veículo para uma dada viagem em função da distância percorrida, X quilómetros.
OBSERVAÇÃO
Acautele o eventual caso de o utilizador atribuir um número negativo à variável X, isto é, garanta o domínio da variável X.
Passo 4
IMPLEMENTAÇÃO DO ALGORITMO:
- Abra um novo documento da TI-Nspire CX II T.
- Crie uma nova página com o editor de programas da aplicação Python, designe o programa por “CUSTO” e de seguida pressione
 para validar.
para validar. - Divida a página em duas aplicações (editor Python, interpretador Python), esquema de página na horizontal, como já realizado na Unidade 1.
- Na página do editor de Python, clique na tecla
 , depois selecione a opção 4: Planos integrados, seguida da opção 1: Funções e, por fim, a opção 1: def function().
, depois selecione a opção 4: Planos integrados, seguida da opção 1: Funções e, por fim, a opção 1: def function().
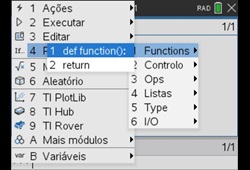
Passo 5
- Designe a função por C(X), função de um argumento.
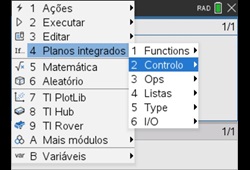
- De seguida clique na tecla
 , depois selecione a opção 4: Planos integrados, e por fim a opção 2: Controlo.
, depois selecione a opção 4: Planos integrados, e por fim a opção 2: Controlo. - Selecione, por fim, a função condicional 3: if … elif … else .
- Observe a indentação automática da estrutura que constitui a função condicional selecionada.
- Complete a função condicional baseando-se no algoritmo proposto para esta tarefa.
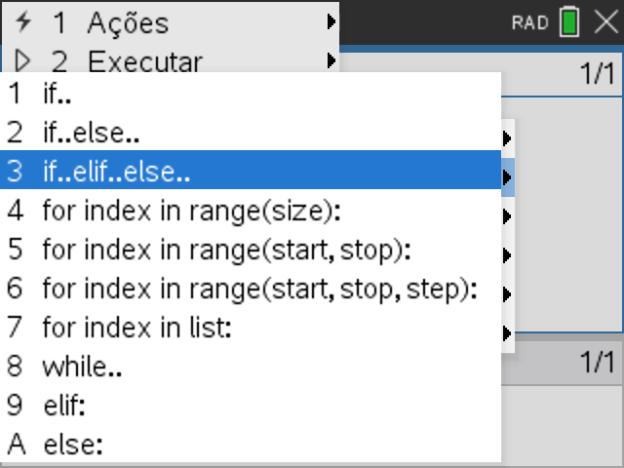
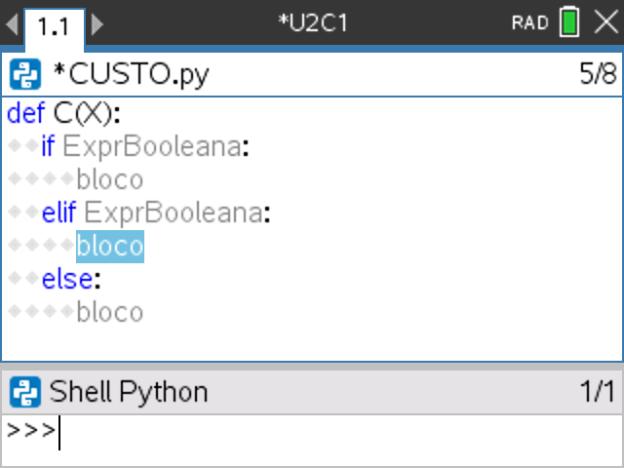
Passo 6
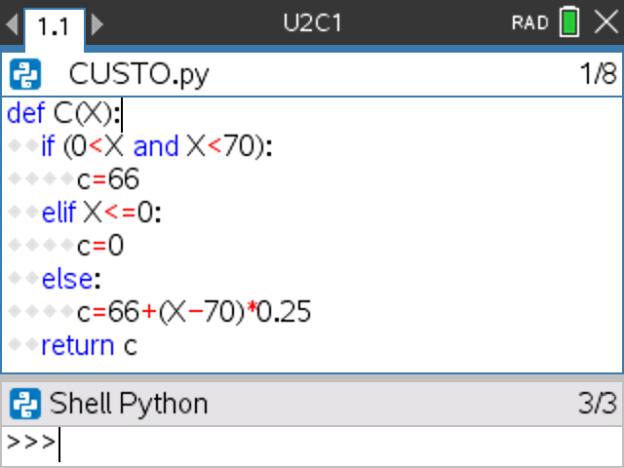
- Utilize a tecla
 para aceder mais facilmente a cada campo, ExprBooleana ou bloco , da função condicional.
para aceder mais facilmente a cada campo, ExprBooleana ou bloco , da função condicional. - Deverá obter o programa que se encontra na figura ao lado.
- Os símbolos operacionais < e <= , e também o operador lógico and, podem obter-se através da opção 3:Ops do submenu 4:Planos integrados. Poderão, também, ser facilmente obtidos através do teclado da unidade portátil, pressionando sucessivamente as teclas
 e
e 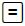 .
.
Passo 7
- Pressione simultaneamente as teclas
 e
e  para verificar a sintaxe e guardar o programa.
para verificar a sintaxe e guardar o programa.
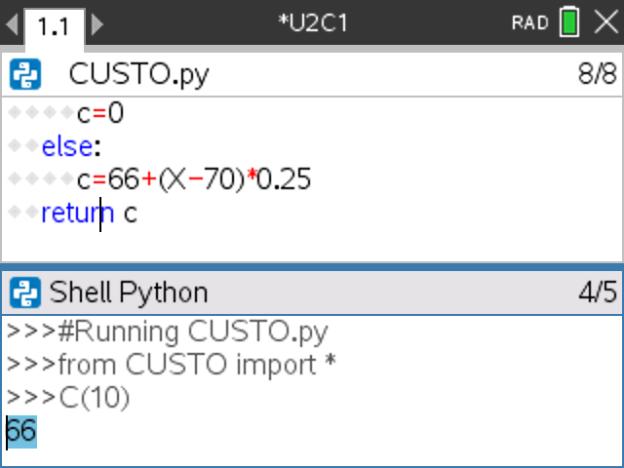
- Execute o programa, clicando simultaneamente nas teclas
 e
e  ou colocando o cursor no interpretador (Shell Python), para determinar o custo de uma viagem com um veículo alugado nesta empresa.
ou colocando o cursor no interpretador (Shell Python), para determinar o custo de uma viagem com um veículo alugado nesta empresa.
Passo 8
OBSERVAÇÃO
O atalho ![]() e
e ![]() guarda a atualização do programa construído na aplicação TI-Python, mas não guarda o documento tns. Para guardar o documento tns, com todas as páginas que o compõem, deve usar o atalho teclas
guarda a atualização do programa construído na aplicação TI-Python, mas não guarda o documento tns. Para guardar o documento tns, com todas as páginas que o compõem, deve usar o atalho teclas ![]() e S ou usar a opção adequada após pressionar a tecla
e S ou usar a opção adequada após pressionar a tecla ![]() .
.

Passo 9
APLICAÇÃO DAS APRENDIZAGENS:
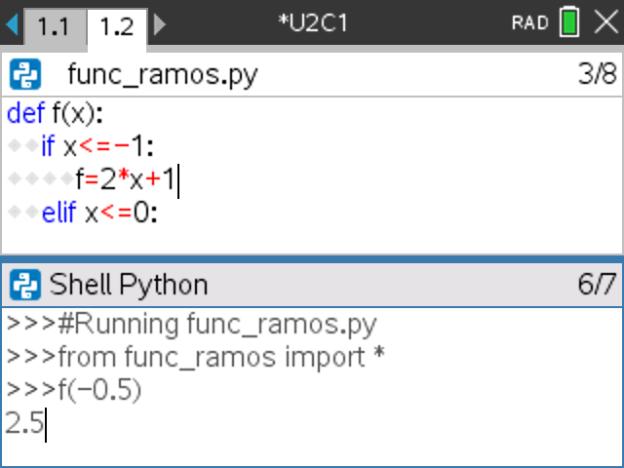
Funções definidas por ramos
Seja f uma função, real de variável real, definida por ramos por:

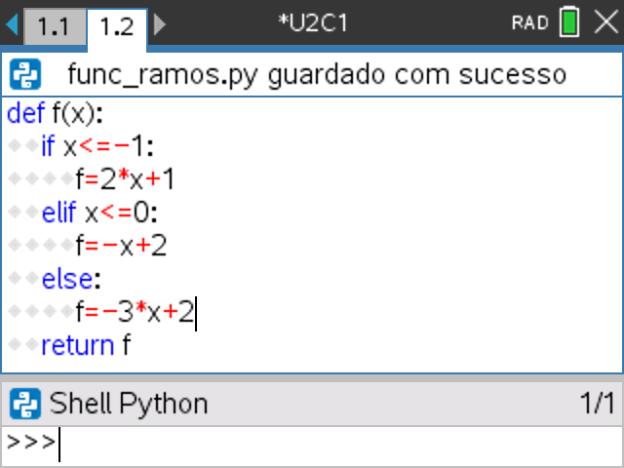
Lição 2: O ciclo FOR
Descarregar documentos do professor / alunoNesta segunda lição da Unidade 2 vamos descobrir como repetir um procedimento ou um conjunto de instruções utilizando um ciclo FOR.
Objetivos:
- Explorar e implementar o ciclo FOR
- Utilizar o ciclo FOR em exemplos simples
Passo 1
Por vezes, num programa, é útil e/ou necessário repetir uma ou várias instruções um certo número finito de vezes. Se o número de repetições do processo é conhecido, então utilizamos um ciclo limitado FOR.
A sintaxe de um ciclo FOR é a seguinte:

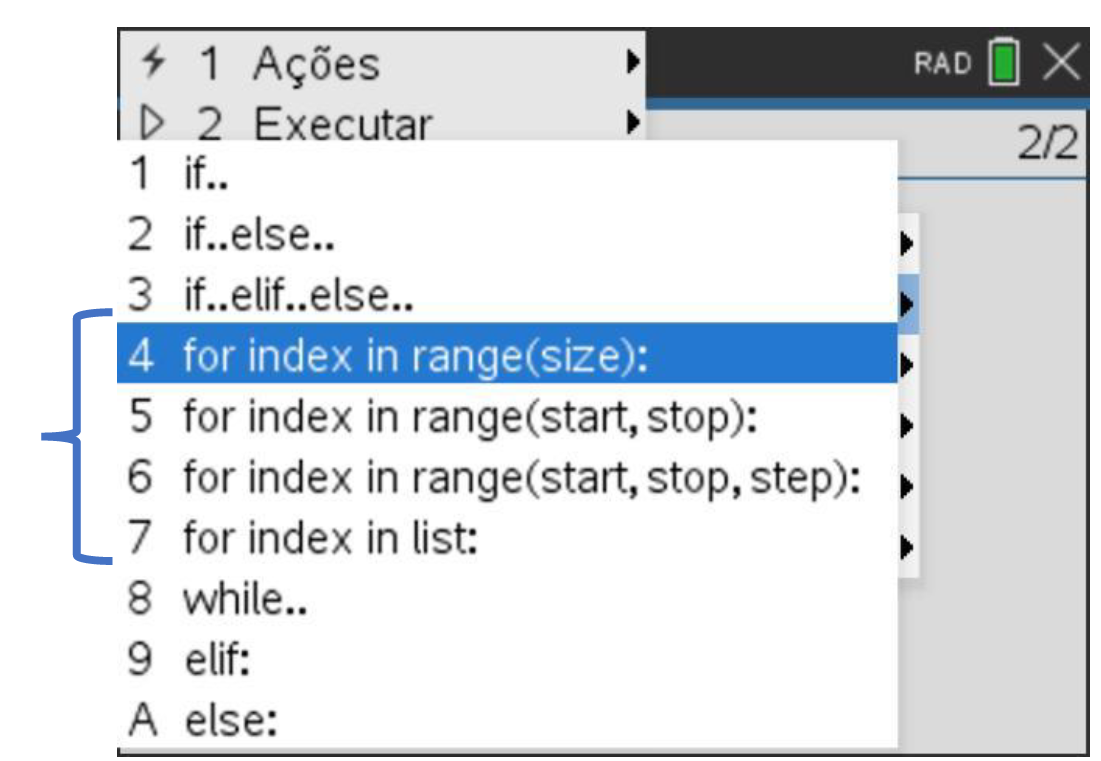
Passo 2
A função range() permite, através dos seus argumentos, definir enumeras formas de se implementar o ciclo FOR. Conforme imagem do passo anterior, este ciclo pode ser executado das seguintes formas:
- for i in range(n): a variável i toma os valores inteiros de 0 até n–1, isto é, toma n valores.
- for i in range(início, fim): a variável i toma os valores inteiros de início até fim–1, onde início e fim são os argumentos da função.
- for i in range(início, fim, passo): a variável i toma os valores inteiros desde início até fim–1, obtidos por um incremento de passo, onde início, fim e passo são os argumentos da função.
- for i in lista: a variável i toma os valores da lista, começando pelo primeiro até ao último.
Não existe nenhuma instrução para indicar o fim de ciclo. Faz-se pela indentação, ou seja, o deslocamento para a direita de uma ou mais linhas é que assinala o fim do ciclo.
Passo 3
EXEMPLO:
Ao estudar sequências e regularidades numéricas, foi colocado a um aluno do ensino básico o seguinte desafio:
Elabora um programa que crie uma lista
com cinco primeiros quadrados perfeitos
não negativos.

Passo 4
IMPLEMENTAÇÃO DO ALGORITMO:
Vamos criar um programa para se entender melhor o que é um ciclo, assim como, o que é um processo iterativo.
- Inicie um novo programa em Python e designe-o por “CICLO”.
- Crie uma lista vazia escrevendo a instrução b = [ ]. Na linguagem Python, os elementos de uma lista são colocados entre [ ] (parêntesis retos), separados por vírgulas.
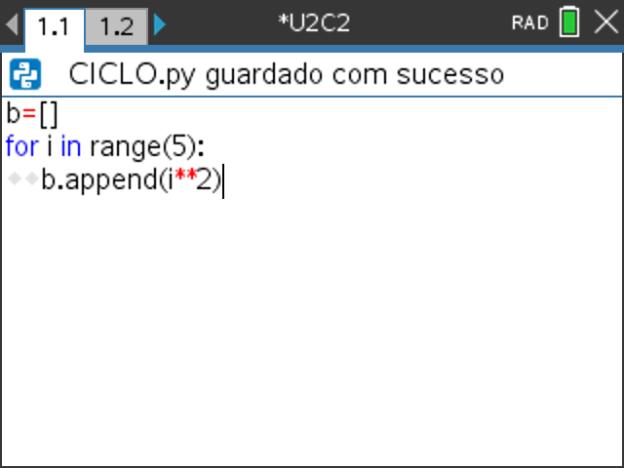
Passo 5
- Depois clique na tecla
 e selecione submenu 4: Planos integrados, depois 2: Controlo, e por fim a opção 4: for index in range(size):.
e selecione submenu 4: Planos integrados, depois 2: Controlo, e por fim a opção 4: for index in range(size):. - A função .append( ) permite o preenchimento de uma lista. Assim, b.append(i**2) acrescenta à lista b um novo elemento com o quadrado de i. Isto é, para cada valor de i, o valor de i2 é acrescentado ao fim da lista.
- A variável i varia ente 0 e 4, o que corresponde a um ciclo de 5 valores, e, portanto, a acrescentar à lista b cinco elementos.
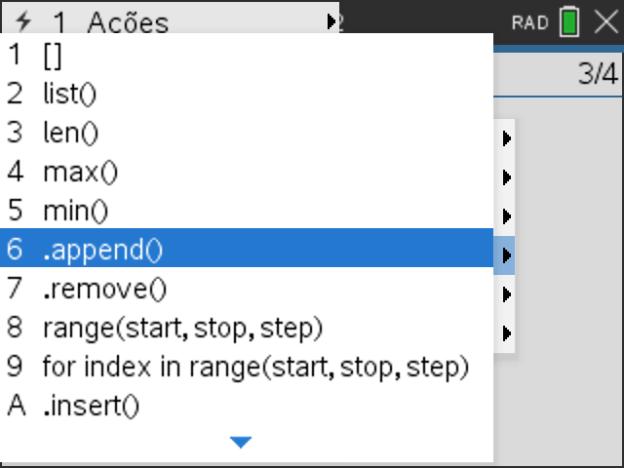
Passo 6
OBSERVAÇÃO:
De notar que, o contador do ciclo FOR é, por defeito, inicializado em 0. A função .append() aplica-se apenas a listas, sendo a sua sintaxe: nomelista.append(elemento a acrescentar). Pode-se aceder a esta função através do menu, pressionando tecla ![]() , de seguida opção 4: Planos integrados, depois a opção 4: Listas e, por fim, selecionar 6: .append().
, de seguida opção 4: Planos integrados, depois a opção 4: Listas e, por fim, selecionar 6: .append().
- Pressione simultaneamente as teclas
 e B para verificar a sintaxe e guardar o programa.
e B para verificar a sintaxe e guardar o programa. - Execute o programa, clicando simultaneamente nas teclas
 e R , abrir-se-á uma nova página com o interpretador de Python (Shell) onde foi executado o programa.
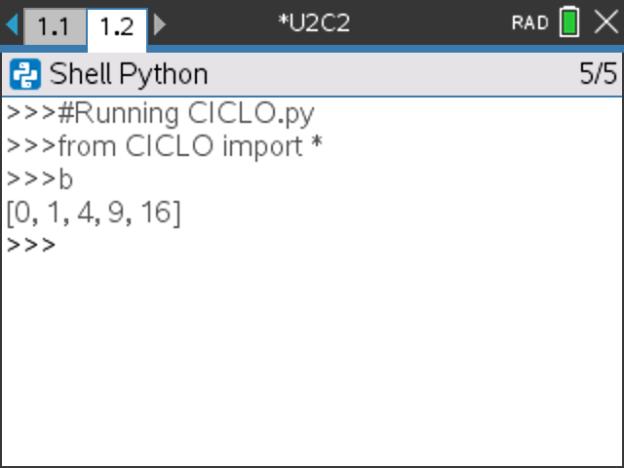
e R , abrir-se-á uma nova página com o interpretador de Python (Shell) onde foi executado o programa. - Por fim, obtenha a lista b, escrevendo o seu nome na linha de comando do Shell e pressionando

OBSERVAÇÃO:
Num ciclo ou numa outra qualquer estrutura de uma função com instruções com recuo, qualquer escrita recuada de um comando faz parte do ciclo ou da função. O fim do ciclo ou da função é definido pela saída do recuo.
Passo 7
APLICAÇÃO DAS APRENDIZAGENS:
Sequências com Construção com Fósforos
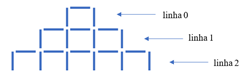
Na construção abaixo, a primeira linha, denominada "linha 0", é formada por 3 fósforos (2 na vertical e 1 na horizontal), a segunda linha por 7 fósforos (4 na vertical e 3 na horizontal), a “linha 2” (3ª linha) por 11 fósforos, e assim sucessivamente.
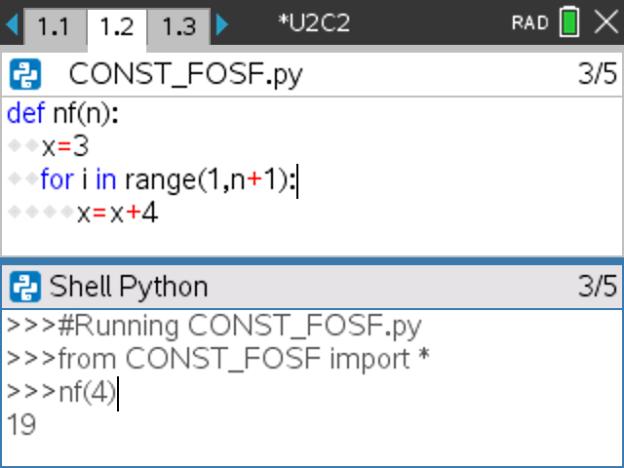
Passo 8
Por quantos fósforos será formada a linha 4?
Construa um programa que, usando um ciclo FOR, permita obter o número de fósforos numa dada linha desta construção.
Execute o programa para obter o número de fósforos que contém a centésima linha.
SUGESTÃO:
Pode aceder a variáveis ou funções definidas num programa, antes ou depois de o executar no interpretador, pressionando a tecla ![]() .
.
Lição 3: O ciclo não limitado WHILE
Descarregar documentos do professor / alunoNesta terceira lição da Unidade 2 vamos descobrir como repetir um procedimento ou um conjunto de instruções utilizando um ciclo não limitado WHILE.
Objetivos
- Explorar e implementar o ciclo não limitado WHILE
- Utilizar o ciclo WHILE em exemplos simples
Passo 1
Por vezes, num programa, é útil e/ou necessário repetir uma ou várias instruções um número, não previamente definido, de vezes. Se o número de repetições do processo não é conhecido, então utilizamos um ciclo não limitado WHILE.
A sintaxe de um ciclo WHILE é a seguinte:
ALGORITMO
Enquanto a condição for verdadeira:
Instrução1
Instrução2
…
Passo 2
LINGUAGEM PYTHON
while condição
Instrução1
Instrução2
…
Não existe nenhuma instrução para indicar o fim de ciclo. Faz-se pela indentação, ou seja, o deslocamento para a direita de uma ou mais linhas é que assinala o fim do ciclo.
Passo 3
EXEMPLO:
Termos de uma sucessão definida por recorrência.
Elabore um programa que permita determinar qual a ordem, n, do maior termo inferior a 1 da sucessão definida por recorrência por:


Passo 4
IMPLEMENTAÇÃO DO ALGORITMO:
Vamos criar um programa para se entender melhor o que é um ciclo, assim como, o que é um processo iterativo.
- Inicie um novo programa em Python e designe-o por “CICLO_ILIM”.
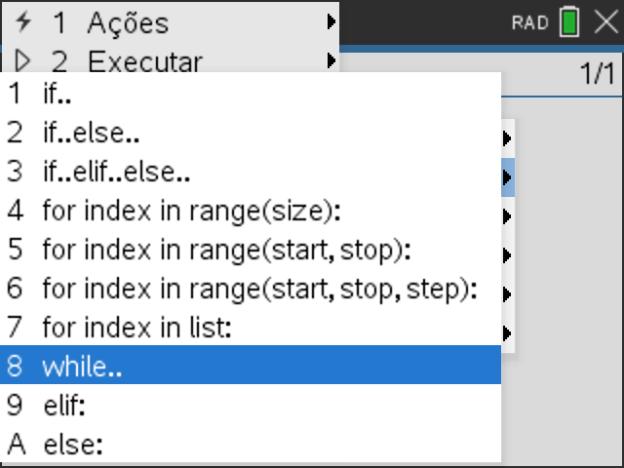
- A função While acede-se clicando na tecla
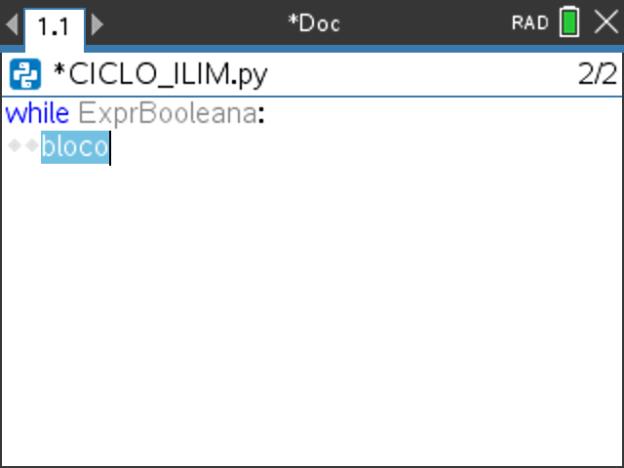
 e selecione submenu 4: Planos integrados, depois 2: Controlo, e por fim a opção 8: while.. , desta forma surgirá já a sua estrutura com os campos para preencher.
e selecione submenu 4: Planos integrados, depois 2: Controlo, e por fim a opção 8: while.. , desta forma surgirá já a sua estrutura com os campos para preencher.
Passo 5
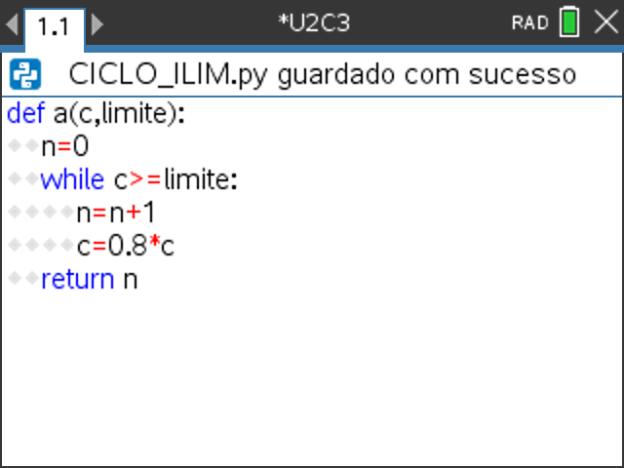
- Enquanto a variável c, termo da sucessão, for superior ou igual ao limite, a variável n, ordem do termo, será incrementada em 1.
- Para tal, defina uma função em Python de forma que entrados dois valores, termo inicial e limite, se obtenha o número de termos inferiores ao valor do limite.
- Pressione simultaneamente as teclas
 e B para verificar a sintaxe e guardar o programa.
e B para verificar a sintaxe e guardar o programa.
Passo 6
- Execute o programa, clicando simultaneamente nas teclas
 e R. Abrir-se-á uma nova página com o interpretador de Python (Shell) onde foi executado o programa.
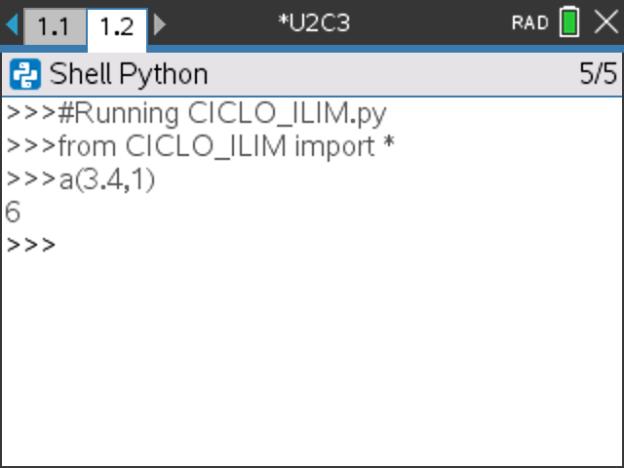
e R. Abrir-se-á uma nova página com o interpretador de Python (Shell) onde foi executado o programa. - No Shell pode agora usar a função a definida no programa CICLO_ILIM.
- Determine, pela função a, a resposta ao problema, isto é, a(3.4,1).
Passo 7
APLICAÇÃO DAS APRENDIZAGENS:
Os ressaltos da bola saltitona
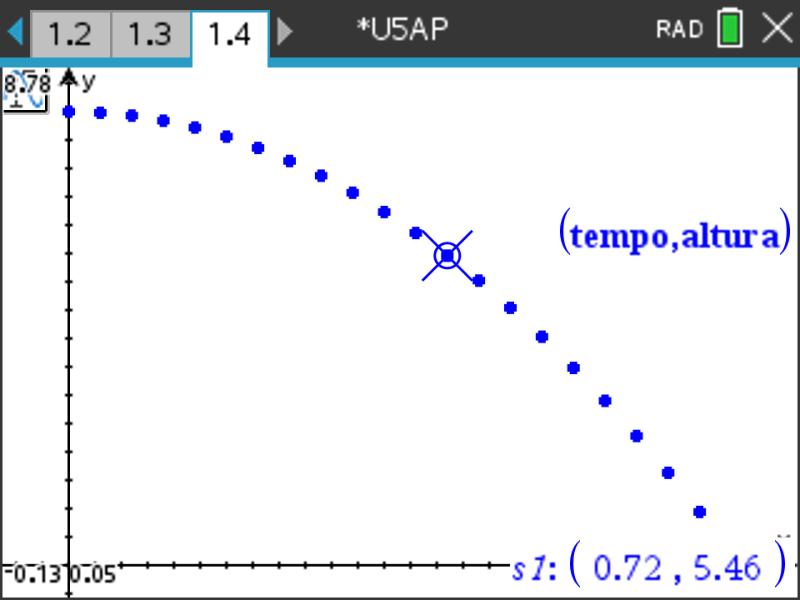
Uma bola é largada no ar a uma altura de 1,20 metros e ressalta no solo atingindo uma altura de 40% da altura do ressalto anterior.
Elabore um algoritmo que permita obter o número de ressaltos realizados até a altura atingida pela bola ser estritamente inferior a 1 cm.
Passo 8
Baseie-se nos seguintes passos:
- Defina uma variável h na qual se guarde a altura do ressalto, em cm, e uma variável r para guardar o número de ressaltos.
- Terá que ser repetido o cálculo da altura, "h toma o valor 0.40 × h", várias vezes sem que se saiba antecipadamente o número de repetições.
- Após cada cálculo será testada a condição h≥1, sendo que o ciclo de repetição dos cálculos será executado enquanto a condição for verdadeira.

Passo 9
IMPLEMENTAÇÃO DO ALGORITMO:
Vamos, agora, construir o programa na linguagem Python, usando o editor da aplicação TI-Python.
- Inicie um novo programa em Python e designe-o por “RESSALTOS”.
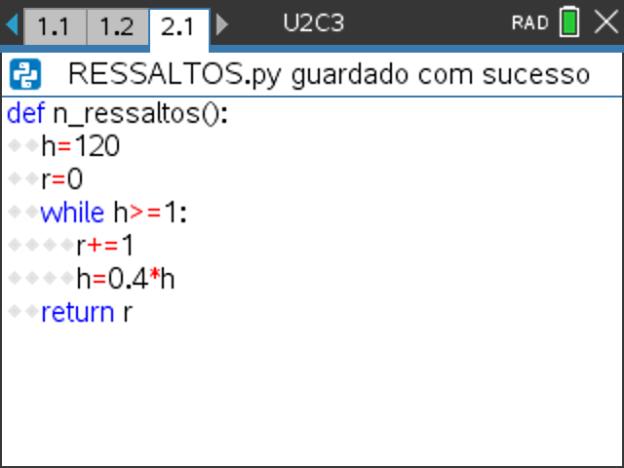
- Propõe-se que use uma função. Teremos, assim, o cuidado de respeitar a indentação (um para o ciclo While e um segundo para a função return) e obteremos no fim o valor da variável r.
Passo 10
- Construa a função n_ressaltos, desta vez será uma função sem argumentos, começando por atribuir os valores iniciais às variáveis h e r.
- De seguida coloque o ciclo não limitado While, colocando a condição e as respetivas linhas de instrução.
- Pressione simultaneamente as teclas
 e
e  para verificar a sintaxe e guardar o programa.
para verificar a sintaxe e guardar o programa.
Passo 11
- Execute o programa, clicando simultaneamente nas teclas
 e
e  . Depois, na página do interpretador, escreva o nome da função ou clique na tecla
. Depois, na página do interpretador, escreva o nome da função ou clique na tecla  e selecione a função e prima
e selecione a função e prima 
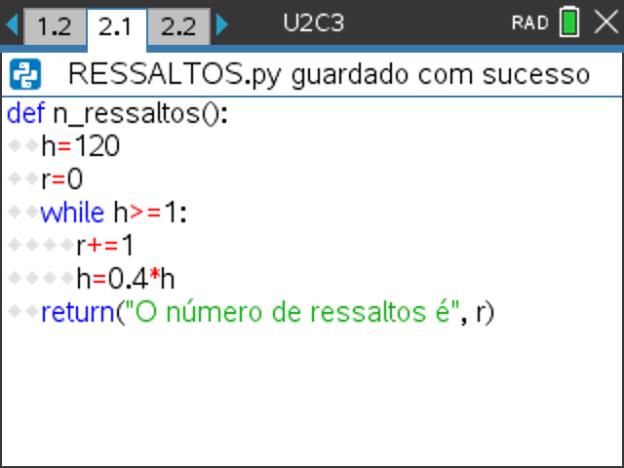
- Enriqueça o programa acrescentando uma mensagem, por exemplo: “O número de ressaltos é “. Para tal, no editor acrescenta à função return o texto pretendido, isto é, escreva:
•• return (“O número de ressaltos é “, r )
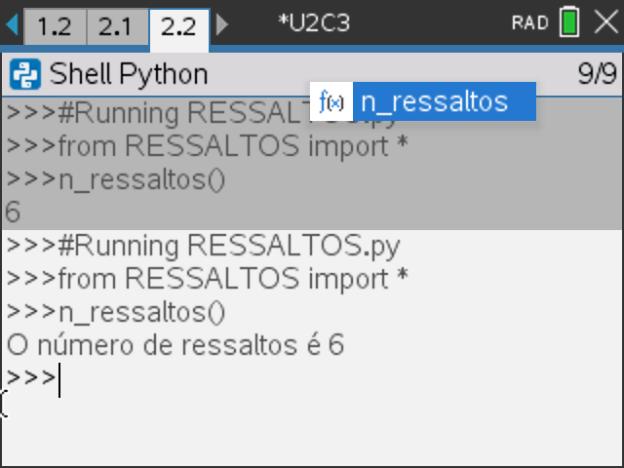
Passo 12
ATENÇÃO:
Pode ser necessário manter os valores intermédios dos cálculos, para por exemplo serem reutilizados ou simplesmente ficarem guardados (termos de uma sequência numérica, por exemplo). Nesse caso será recomendável a utilização de listas, sendo no exemplo anterior o valor pretendido o último elemento dessa lista.
UM DESAFIO:
Enriquecer o programa anterior, RESSALTOS, de forma a obter-se a distância total percorrida pela bola até ela parar, assumindo que os ressaltos da bola apenas registam deslocamentos verticais.
Aplicação: Ciclos e Testes
Descarregar documentos do professor / alunoNesta Aplicação da Unidade 2, propõe-se que utilize as noções trabalhadas nas lições sobre funções condicionais, bem como ciclo limitados e não limitados.
Objetivos:
- Utilizar os ciclos While e For para implementar algoritmos para a resolução de problemas de probabilidades e de estatística.
Passo 1
Nesta aplicação iremos elaborar um programa que permita:
- obter um número aleatório criando, para tal, uma função que designaremos lançamento.
- utilizar esta função num outro programa de forma a determinar o número de lançamentos necessários para obter uma soma de 12 ao lançar 2 dados cúbicos perfeitamente equilibrados e numerados de 1 a 6.
- ao lançar um único dado de 6 faces, se obtenha o número de vezes que cada face saiu, permitindo-se desta forma calcular a frequência relativa e comparar com a probabilidade teórica.

Passo 2
Lançamento de um Dado
- Note que o recurso a funções da TI-Nspire CX com números aleatórios requer, na aplicação TI-Python, a ativação do módulo aleatório.
- Abra um novo documento da TI-Nspire CX II T.
Passo 3
- Crie uma nova página com o editor de programas da aplicação Python, designe o programa por “Lancamento” e de seguida pressione
 para validar.
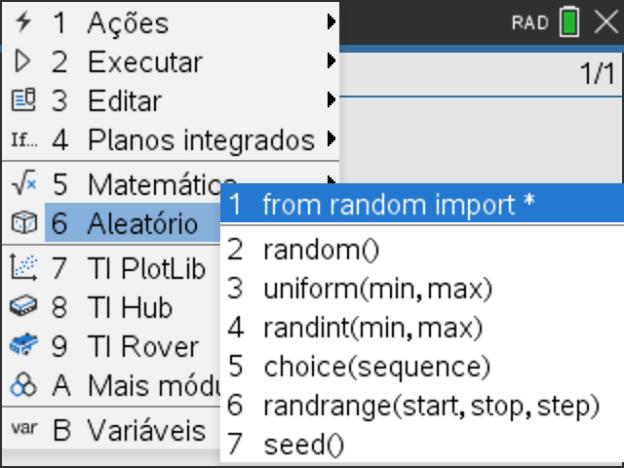
para validar. - Ative o módulo aleatório pressionando a tecla
 e selecionando de seguida a opção 6: Aleatório e depois a opção 1: from random import*.
e selecionando de seguida a opção 6: Aleatório e depois a opção 1: from random import*. - Defina, agora, a função lance() que permita obter um número inteiro aleatório entre 1 e 6, usando a função aleatória randint() da TI-Nspire CX.
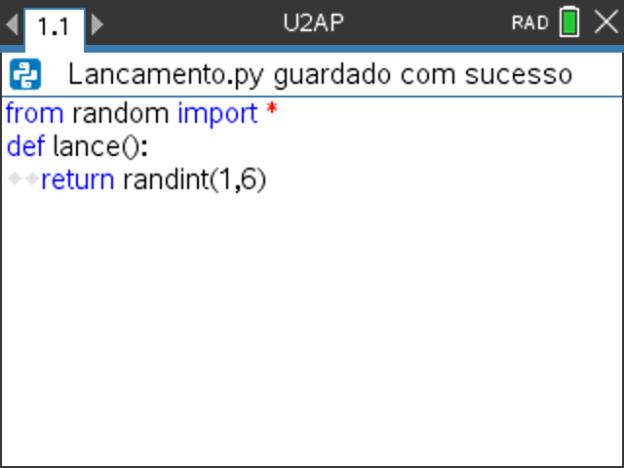
Passo 4
- Teste a função lance(), depois de verificar e guardar o programa.
- Utilize a tecla para cima,
 , para deslocar o cursor para cima e executar novamente a função ou utiliza a tecla
, para deslocar o cursor para cima e executar novamente a função ou utiliza a tecla  , ou ainda, escreva o nome da função.
, ou ainda, escreva o nome da função.
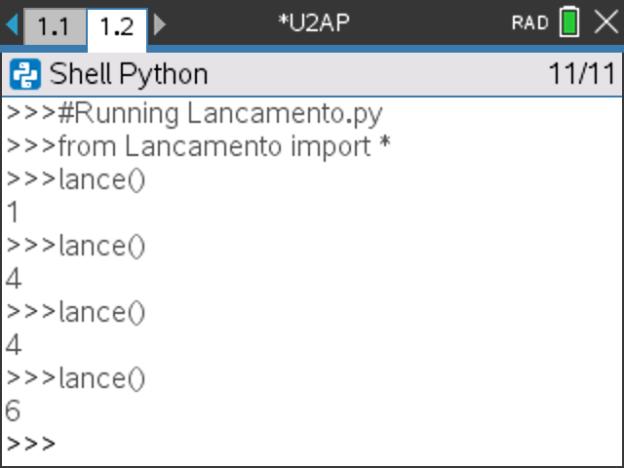
Passo 5
Número de lançamentos necessários.
Lance dois dados de 6 faces, cubos perfeitamente equilibrados e com as faces numeradas de 1 a 6, e adicione os dois resultados obtidos. Escreva outro programa para simular os lançamentos desses dois dados e encontrar o número n de lançamentos realizados até obter a soma 12.
Existem muitas soluções possíveis, mas a primeira que vem à mente é reutilizar a função anterior.
- Utilize-se a variável s para guardar a soma das faces em cada lançamento e a variável n para guardar o número de lançamentos necessários até a soma ser 12.
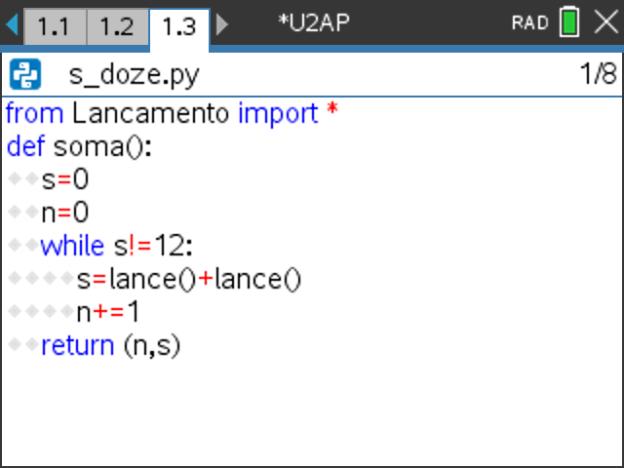
Passo 6
- Na linguagem Python o símbolo de diferente,
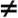 , é representado por != . Este símbolo pode ser obtido clicando na tecla
, é representado por != . Este símbolo pode ser obtido clicando na tecla  , seguido da opção 4: Planos integrados e por fim a opção 3: Ops, ou ainda usando o atalho
, seguido da opção 4: Planos integrados e por fim a opção 3: Ops, ou ainda usando o atalho  e
e 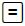 com o teclado da unidade portátil.
com o teclado da unidade portátil. - Construa a função soma(), numa nova página de editor de Python ou dentro do programa Lancamento, recorrendo a um ciclo While e à função lance(). Certifique-se que ativado o programa Lancamento e que é respeitada a indentação e, em seguida, execute-a.
- O resultado é um par ordenado em que o primeiro elemento indica o número de lançamentos necessários até sair soma 12, e o segundo elemento indica o valor da soma atingido, neste caso 12.
Passo 7
Amostragens e frequências
Acabamos de observar, no exemplo anterior, que o número de lançamentos necessários para se obter a soma 12 é variável. Podemos, portanto, proceder ao cálculo da frequência relativa da soma 12 para uma dada amostragem, que, para um grande número de simulações, deve tender para a probabilidade teórica.
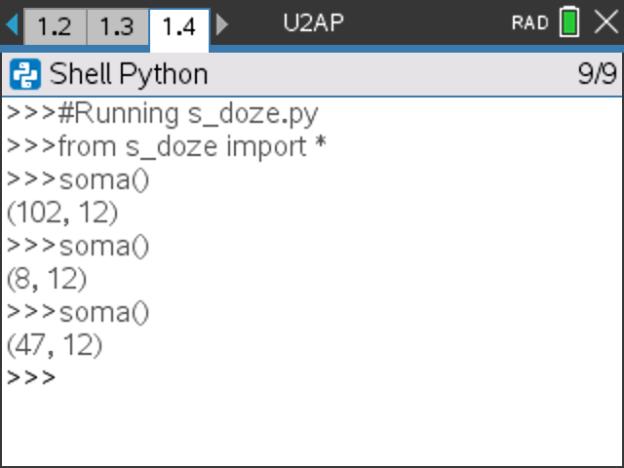
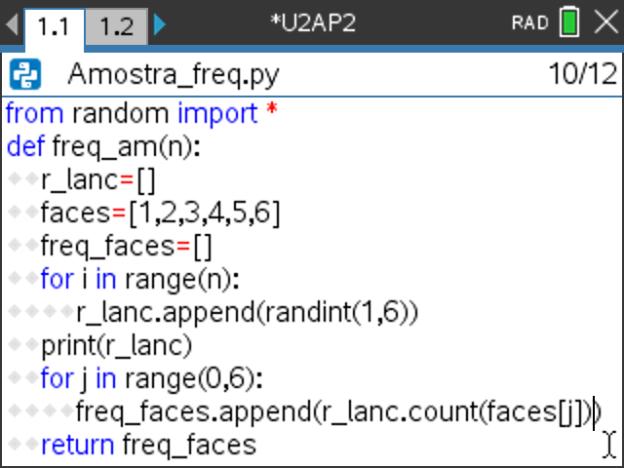
- Adicione uma nova página com o editor de Python, designe o programa por Amostra_freq.
- Use uma função, cujo argumento será o número de simulações do lançamento do dado e que poderemos designar por n, para obter as frequências absoluta de cada valor numérico da face, de 1 a 6.
Passo 8
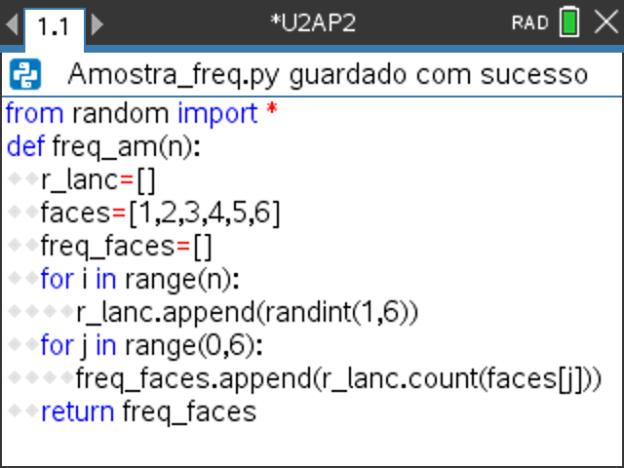
- Nesta função, o resultado de cada lançamento deverá ser armazenado numa lista r_lanc, previamente inicializada como vazia pela instrução r_lanc = [ ] .
- Também as faces do cubo, os números de 1 a 6, devem ser guardados inicialmente numa lista faces, colocando a instrução faces=[1, 2, 3, 4, 5, 6].
- De seguida, usando um ciclo FOR são realizadas as n simulações do lançamento de um dado cúbico numerado de 1 a 6, sendo guardados todos resultados na lista r_lanc.
Passo 9
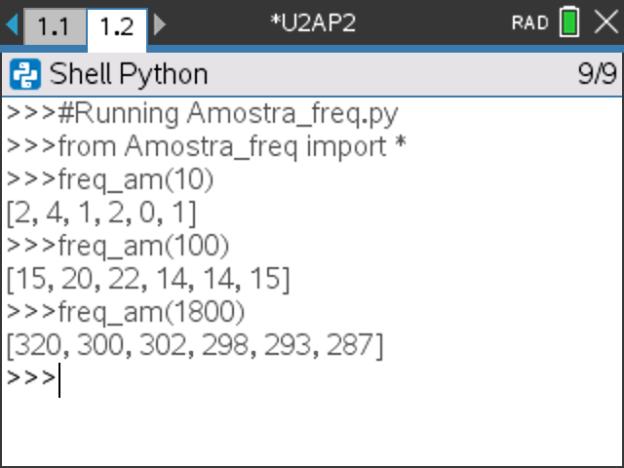
- Por fim, e através novamente de um ciclo FOR, é criada uma instrução que para cada um dos valores da variável (1 a 6) conta quantas ocorrências na lista r_lanc são iguais a esse valor. Essa contagem deverá ser guardada numa nova lista, freq_faces, que deve ser criada no início da função como uma lista vazia.
- Pressione simultaneamente as teclas
 e B para verificar a sintaxe e guardar o programa. Não se esqueça também de usar o atalho
e B para verificar a sintaxe e guardar o programa. Não se esqueça também de usar o atalho  e S para guardar o documento.
e S para guardar o documento.
Passo 10
- Execute o programa, clicando simultaneamente nas teclas
 e
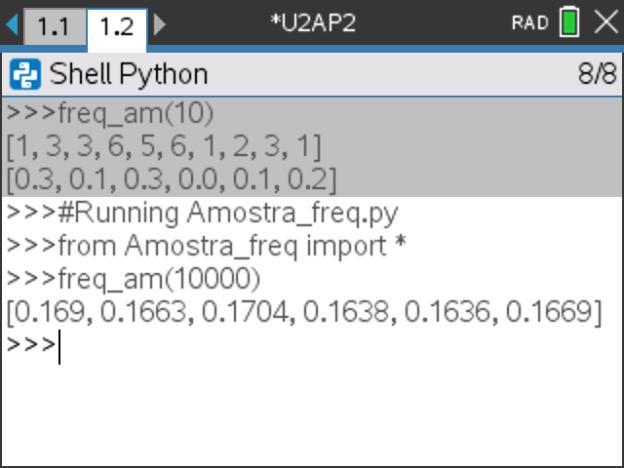
e  . Abrir-se-á uma nova página com o interpretador de Python (Shell) onde foi executado o programa. Por fim execute a função freq_am(), colocando como seu argumento o número de simulações pretendidas, e observará a lista das frequências absolutas.
. Abrir-se-á uma nova página com o interpretador de Python (Shell) onde foi executado o programa. Por fim execute a função freq_am(), colocando como seu argumento o número de simulações pretendidas, e observará a lista das frequências absolutas. - Opcionalmente poderá adaptar o programa de forma a apresentar a frequência absoluta de um só dos valores da variável e/ou apresentar as frequências relativas. Ou então, por exemplo, tornar visível os resultados de todas as n simulações, que poderá ter alguma vantagem para a verificação com poucas simulações.
- Lição 1
- Lição 2
- Lição 3
- Aplicação
Unidade 3: Iniciação à programação em Python
Lição 1: Funções e Ciclos
Descarregar documentos do professor / alunoNesta primeira lição da Unidade 3, aplicará o conhecimento de algoritmos e da linguagem Python para:
- Procurar soluções de uma equação f(x) = 0
- Resolver um problema de otimização.
Objetivos:
- Utilizar uma função em linguagem Python.
- Implementar o ciclo While.
Passo 1
Método da Bisseção
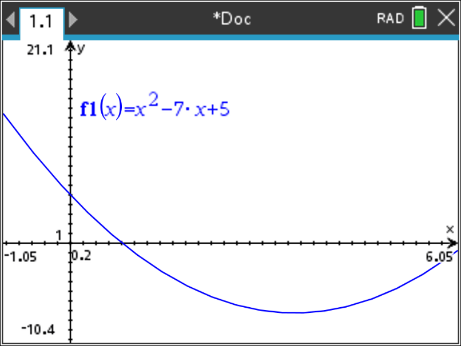
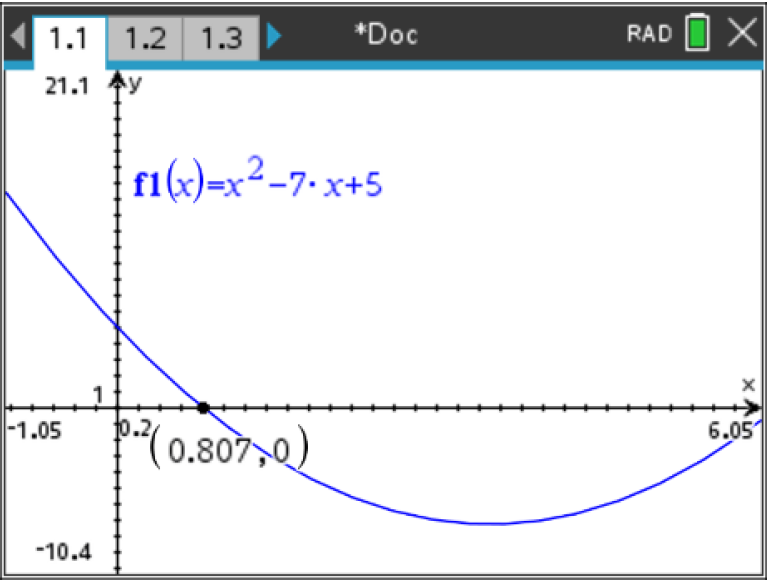
Considere a função f definida em em [-2, 3] por f(x) = x2 - 7x + 5.
Utilize a calculadora para traçar uma curva Cf representação gráfica da função f.
Iremos resolver a equação f(x) = 0 com um programa em Python, que vai escrever, correspondente a um algoritmo conhecido por "método da bisseção".
Passo 4
IMPLEMENTAÇÃO DO ALGORITMO:
- Enquadrar entre dois números inteiros, a e b, a solução x0 da equação f(x) = 0 com uma precisão definida (erro máximo), que designaremos de "erro".
- Verificar que f(a) × f(b) < 0 .
- Calcular
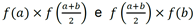
- Concluir se x0 pertence ao intervalo
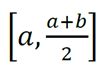 ou ao intervalo
ou ao intervalo 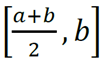
Passo 5
Abra uma nova página da aplicação TI-Python com o editor de programas, designe-o por BISS.
- Introduza as diferentes instruções de código no programa, pode encontrá-las no módulo Planos integrados (clicar na tecla
 depois 4: Planos integrados).
depois 4: Planos integrados). - Os operadores relacionais e lógicos podem obter-se diretamente pressionando
 depois 4: Planos integrados e por fim 3: Ops.
depois 4: Planos integrados e por fim 3: Ops. - [a, b] representa o intervalo de estudo, "erro" o erro máximo admissível.
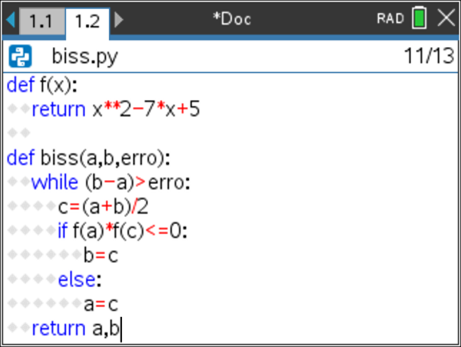
Passo 6
Execute o programa, clicando simultaneamente nas teclas ![]() e
e ![]() , e no interpretador (Shell Python) aplique a função BISS() ao intervalo [0,1] e com erro máximo de 0.01.
, e no interpretador (Shell Python) aplique a função BISS() ao intervalo [0,1] e com erro máximo de 0.01.
Observe o resultado obtido. Teste os resultados apresentados pelo seu programa recorrendo à resolução gráfica da equação na aplicação Gráficos da TI-Nspire™ CX II.
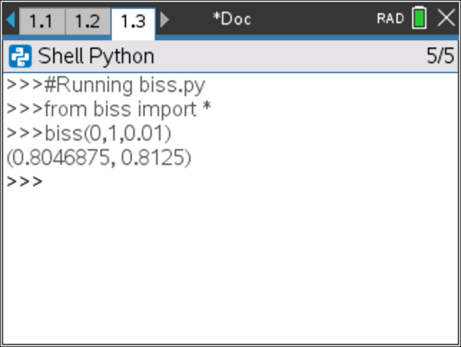
Passo 7
Vá refinando a procura para encontrar uma solução tão próxima quanto a obtida pela resolução gráfica.
O valor exato da solução x0 no intervalo [0, 1] é dado por :x0=(7-√(29 )) / 2
Passo 8
POSSÍVEIS EXTENSÕES:
- Processo Iterativo
Em alternativa a procurar a solução em função de um erro dado, fazê-lo a partir de um número n de iterações.
Passo 9
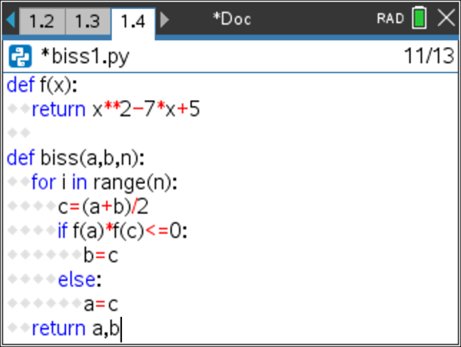
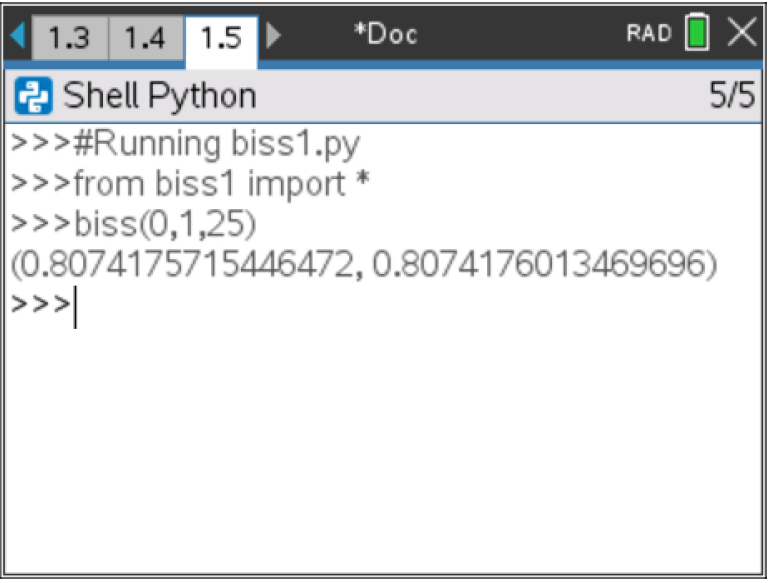
- Comece por fazer uma cópia do programa BISS() e designe-o por BISS1, aliás nome sugerido por defeito. Para duplicar um programa, pressione a tecla
 , em seguida na opção 1: Ações e por fim selecione a opção 3: Criar cópia … . Surgirá uma janela para inserir o nome.
, em seguida na opção 1: Ações e por fim selecione a opção 3: Criar cópia … . Surgirá uma janela para inserir o nome. - Altere no código do programa o ciclo WHILE pelo ciclo FOR adequado, conforme se pode observar no ecrã ao lado.
- O restante código do programa mantem-se igual. Execute o programa e função, compare o resultado obtido com o anterior.
Passo 10
b) Processo Recursivo
Construa um programa em que o processo de procura do intervalo onde se encontra a solução recorra recursivamente a uma mesma função.
Observe a proposta de programa ao lado e construa o programa em TI-Python, experimente-o.
NOTA:
Para mais informações sobre recursividade deve consultar a Lição 3 desta Unidade 3 do projeto “10 Minutos de Código”.

Lição 2: O ciclo FOR
Descarregar documentos do professor / alunoNesta segunda lição da Unidade 3, descobrirá como repetir um processo ou um conjunto de instruções utilizando o ciclo FOR.
Objetivos :
- Aplicar uma função.
- Descobrir como implementar o ciclo FOR
- Utilizar o ciclo FOR em exemplos simples.
Passo 1
Simular uma Experiência Aleatória
Um saco opaco contém seis bolas vermelhas e quatro verdes. Retira-se, ao acaso, uma bola do saco e regista-se a sua cor, de seguida volta-se a colocar a bola no saco.
Crie um programa com uma função cor() que simule esta experiência aleatória de variável X.
- Que valores pode tomar a variável X?
- Pretende-se escrever um programa que, através de uma condição, distinga as bolas vermelhas das bolas verdes.
Passo 2
- Comece um novo programa, com o nome "EXPERIENCIA".
- Como irá trabalhar com números aleatórios, é necessário carregar a biblioteca "random". Para isso, pressionar a tecla
 , depois 6: Aleatório.
, depois 6: Aleatório. - Insira o programa constante no ecrã ao lado no editor de TI-Python, tendo em atenção à necessidade de respeitar a indentação.
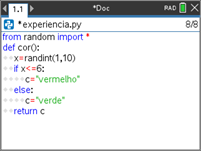
Passo 3
- Executar o programa e, no interpretador (Shell) exibir o resultado da função cor().
- Repita a execução da função cor(), poderá escrever o nome e pressionar
 ou clicar na tecla
ou clicar na tecla  , e analise os resultados.
, e analise os resultados.
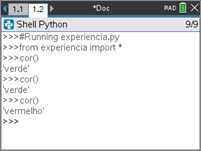
Passo 4
SUGESTÃO:
Este programa pode ser alterado para se poder aplicar a qualquer número de bolas. Neste caso, pode definir-se a função cor(n,a) onde os argumentos representam: n é o número de bolas e a o número de bolas vermelhas.
APLICAÇÃO DAS APRENDIZAGENS:
Amostragem e toma de decisão
Fez-se uma sondagem acerca de um novo espetáculo proposto por um artista. O estudo, realizado numa grande cidade, revelou que dois terços das pessoas que viram o espetáculo gostaram. O agente do artista acredita que toda a população portuguesa pensará da mesma forma. Para verificar o que pensou, solicitou um estudo a uma empresa de sondagens.

Passo 5
Estudo da População
Para realizar o estudo, o estatístico da empresa deve criar uma função que simule a situação.
O vosso trabalho consiste em criar esta função, respeitando as seguintes regras:
- O espetáculo agradou, com uma probabilidade p = 2/3.
- O espetáculo não agradou, com uma probabilidade p = 1/3.
- Comece um novo programa, com o nome SONDAGEM.
- Escreva a função no editor do TI-Python e teste-a várias vezes pressionando
 e depois digite na Shell o nome da função, sem argumentos, resposta() e pressione
e depois digite na Shell o nome da função, sem argumentos, resposta() e pressione 
DICA:
Pode utilizar a tecla ![]() e selecionar a função ou utilizar a tecla de seta para cima,
e selecionar a função ou utilizar a tecla de seta para cima, ![]() , até selecionar a última instrução e clicar
, até selecionar a última instrução e clicar ![]() para repetir a execução (pode ser mais rápido do que digitar o nome da função…).
para repetir a execução (pode ser mais rápido do que digitar o nome da função…).
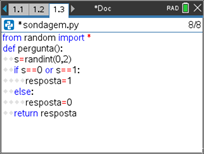
Passo 6
Simulação duma amostra de dimensão n.
A empresa de sondagens pretende simular amostras de dimensões variadas.
Portanto, deve criar no editor de programas uma função experiencia(n) que execute a função pergunta() n vezes, isto é, gere uma amostra de dimensão n.
- Inicie a função com uma instrução que crie uma lista vazia, lista L.
- Preencha esta lista utilizando a função pergunta() e um ciclo For.
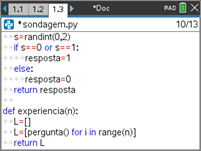
Passo 7
SUGESTÃO:
A linguagem Python permite que se utilize uma função para preencher uma lista incrementada por um ciclo For, como argumento da lista. Processo análogo ao da função seq() usada, nas restantes aplicações da TI-Nspire CX II, para gerar listas.
Este exemplo pode ser feito sem listas. Nesse caso, o programa deve ser ligeiramente alterado para substituir as instruções relativas às listas por ciclos com incremento de uma variável.
- Testar a função experiencia(n) com uma amostra de dimensão 20, executando o programa e escrevendo experiencia(20) no interpretador e pressionando a tecla

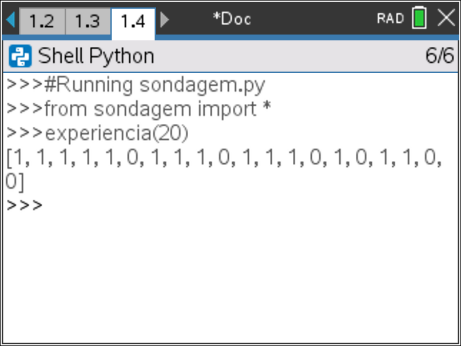
Passo 9
RECORDE QUE:
Para uma dada caraterística estatística, neste caso frequência ou proporção (p ̂), dos elementos de uma amostra, ao seu valor na população designa-se por parâmetro e representa-se por p.
Prova-se que para n ≥ 25 e 0.2 ≤ p ≤ 0.8, a frequência da caraterística na amostra de dimensão n pertence ao intervalo [p-1/√n ;p+1/√n] em 95% dos casos. Este intervalo designa-se “Intervalo de Confiança a 95%”.
A partir do algoritmo da função interv_prev(), escrito em linguagem natural, crie, no programa já iniciado no editor do TI Python, a função interv_prev() .
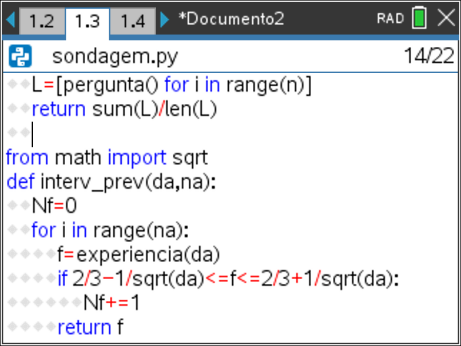
Passo 10
Observe o ecrã ao lado para se orientar.
Execute o programa, atalho ![]() .
.
- No interpretador, pressione a tecla
 para chamar a função interv_prev.
para chamar a função interv_prev. - Teste o programa diversas vezes para amostras de dimensão 100.
- Deduza para dado um exemplo, qual o intervalo de confiança a 95%. Para tal pode seguir a estratégia de fixar a dimensão de cada amostra (da) e variar o número de amostras (na).
- Este estudo estatístico coloca em causa a afirmação do agente do artista?
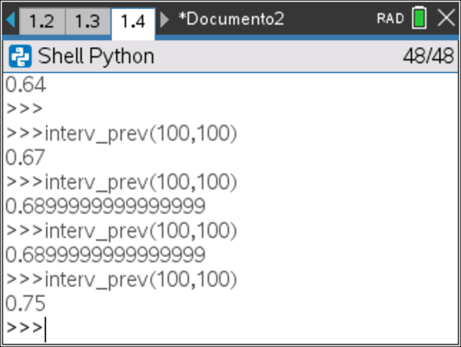
Lição 3: Programação e Recursividade
Descarregar documentos do professor / alunoNesta terceira lição da Unidade 3, aplicará o conhecimento sobre algoritmos e a linguagem Python para programar com recursividade.
Objetivos :
- Aplicar uma função em linguagem Python.
- Implementar programação com recursividade.
Passo 1
Cálculo do Máximo Divisor Comum (Método iterativo)
Para calcular o máximo divisor comum entre dois números naturais a e b, mdc(a,b), utilizaremos o algoritmo de Euclides.
Note-se que consideraremos a > b.
Procederemos da seguinte forma:
- Efetuamos a divisão euclidiana de a por b. Designamos o resto por r (não utilizamos o quociente).
- De seguida trocamos a por b e b por r.
- Enquanto o resto for diferente de 0, repetimos o processo.
Após um determinado número de iterações, obteremos resto 0.
Desta forma, obtemos o mdc(a,b) que será o último resto não nulo do processo recursivo anterior.Passo 2
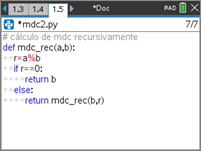
IMPLEMENTAÇÃO DO PROGRAMA:
- Crie um novo programa, designando-o por mdc.
- Crie uma função mdc(a,b) teclando
 , depois 4: Planos integrados e por fim 1: Funções.
, depois 4: Planos integrados e por fim 1: Funções. - O sinal
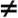 representa-se em linguagem Python por != , que se acede através do menu 4: Planos integrados depois 3: Ops ou pelo atalho
representa-se em linguagem Python por != , que se acede através do menu 4: Planos integrados depois 3: Ops ou pelo atalho  +
+  da unidade portátil.
da unidade portátil.
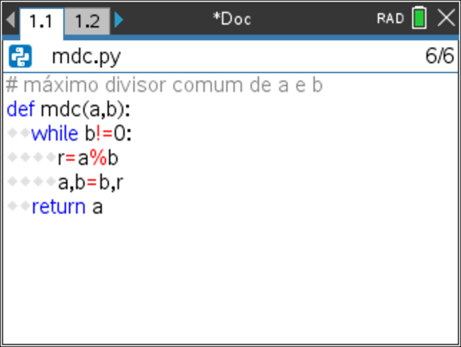
Passo 3
- Note que a atribuição a,b=b,r no programa permite o ganho de uma linha de código, já que corresponde às atribuições a=b e b=r.
- Execute o programa com diferentes pares de números. Verifique a correção dos resultados obtidos.
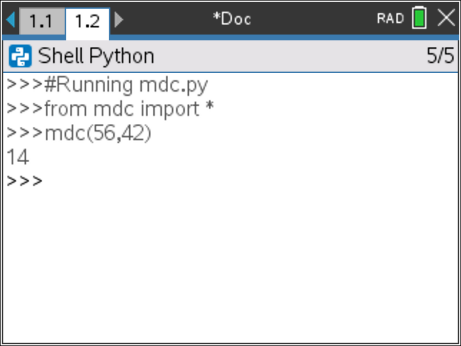
Passo 4
MAIS ALÉM:
Programação com recursividade
Um algoritmo diz-se recursivo quando em algum momento se chama a si próprio.
A recursividade pode ter muitas vantagens num algoritmo. Em primeiro lugar, pode resolver problemas geralmente insolúveis com a utilização apenas de ciclos FOR ou WHILE. Pode ainda tornar um algoritmo mais legível e curto, mas sobretudo permite, em alguns casos, uma grande economia de tempo.
Um primeiro exemplo de recursividade:
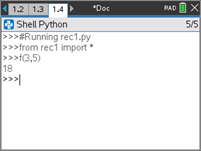
- Crie um novo programa com o nome rec1.
- Escreva o programa que se encontra no ecrã ao lado.
Passo 5
- Quais serão os primeiros casos (valores de 𝒂 e 𝒃) a aplicar este programa? Que resultado obterá?
(Lembre-se de que 𝒂 e 𝒃 são inteiros positivos com 𝒂 > 𝒃)
- O que garante, nesta função recursiva, que o programa vai parar?
- Considere 𝒂=5 e 𝒃=3, efetue manualmente, com papel e lápis, todos os procedimentos desta função. Que resultado obteve?
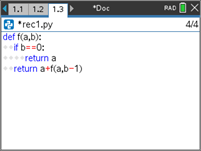
Passo 6
- Execute, agora, o programa, usando o atalho
 , e no interpretador execute a função f.
, e no interpretador execute a função f. - Explore, comparando resultados, situações como f(𝒂,𝒃), f(𝒃,𝒂), f(𝒂,𝒃+c ) e f(𝒂,𝒃)+f(𝒂,c). Que igualdades lhe sugerem?
- O que traduz o resultado da função f(𝒂,𝒃) com 𝒂 e 𝒃 naturais?
Passo 7
Sendo r o resto e q o quociente da divisão euclidiana de a por b teremos que:
a = b*q + r , r < b.
Qualquer divisor comum de a e b é também divisor de r, sendo r = a – b*q, e reciprocamente qualquer divisor comum de b e r divide a = b*q + r.
Assim, o cálculo do mdc(a,b) é reduzido ao cálculo do mdc(b,r), e podemos começar de novo, sem receio, um ciclo recursivo, pois os sucessivos restos constituem uma sequência estritamente decrescente. O último resto não nulo é o mdc pretendido.
Passo 8
Por exemplo, para a=96 e b=81, os cálculos sucessivos obtidos pela função mdc_rec() do programa anterior são os seguintes:
-
mdc_rec(96,81)
r=15 -
mdc_rec(81,15)
r=6 -
mdc_rec(15,6)
r=3 -
mdc_rec(6,3)
r=0 - 3

Passo 9
- Execute o programa, premindo
 , e utiliza a função mdc_rec() com diferentes pares de números naturais.
, e utiliza a função mdc_rec() com diferentes pares de números naturais. - Explore propriedades da função máximo divisor comum recorrendo ao cálculo, através da função mdc_rec(), de um número significativo de casos que lhe permitam formular conjeturas!
IMPORTANTE:
Para evitar ciclos viciosos, sem fim, uma função recursiva deve sempre incluir um caso particular em que o resultado é calculado diretamente, ou seja, sem chamada recursiva; deve-se também garantir que este caso particular seja sempre atingido no final.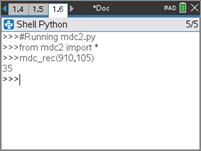
Aplicação: Ciclos e Testes
Descarregar documentos do professor / alunoNesta aplicação da Unidade 3, utilizará os conhecimentos adquiridos nas lições anteriores para implementar algoritmos no editor de programas da aplicação TI-Python, revisitando os conhecimentos sobre números, em particular sobre números primos.
Objetivos :
- Implementar ciclos e testes na programação completa de um algoritmo em Python.
Passo 1
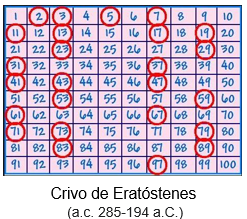
Números Primos
Um número natural diz-se número primo quando tem exatamente dois divisores: 1 e ele próprio.
Por exemplo:
- 1 não é primo (tem apenas um divisor, o 1)
- 7 é um número primo (os seus únicos divisores são 1 e 7).
- 8 não é primo (tem quatro divisores: 1, 2, 4 e 8)
Os números primos são: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …
Há um número infinito de primos.
Passo 2
Pretende-se saber qual é o número primo de ordem 2020.

Passo 3
Pretende-se saber qual é o número primo de ordem 2020.

Passo 4
- Começar um novo programa, no editor TI-Python, e designá-lo por np.
- Escrever as diferentes instruções, respeitando a indentação, conforme ecrã ao lado.
- Note que é necessário embeber o módulo Matemática (tecla
 , seguida de opção 5: Matemática e por fim opção 1: from math import*), por serem utilizadas função matemáticas, como raiz quadrada.
, seguida de opção 5: Matemática e por fim opção 1: from math import*), por serem utilizadas função matemáticas, como raiz quadrada.
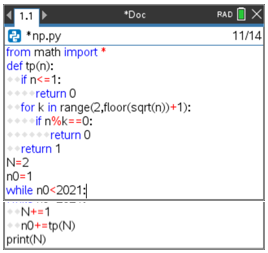
Passo 5
RECORDE QUE:
A incrementação de uma dada variável poderá ser realizada, em linguagem Python, por pelos menos as duas seguintes formas: i = i + inc ou i+=inc , em que inc é o valor do incremento.
SUGESTÃO:
Alterando o ciclo FOR para desde 2 até à parte inteira de raiz quadrada de n mais 1 ( parte inteira (sqrt(n) + 1) ), o que garante o teste a todos os possíveis divisores), diminuímos consideravelmente o tempo de espera, que cai alguns segundos.
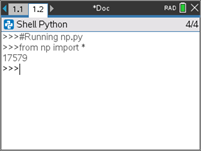
- Execute o programa, e obtenha no interpretador o resultado.
- Verifique que o 2020o número primo é 17579.
- Poderá obter, agora, o número primo de qualquer ordem. Experimente com casos conhecidos, por exemplo o 5º número primo, e com casos seus desconhecidos, por exemplo o 1000º número primo.
- Lição 1
- Lição 2
- Lição 3
- Aplicação
Unidade 4: Utilização da biblioteca TI PlotLib
Lição 1: Configurar uma representação
Descarregar documentos do professor / alunoNesta primeira lição da Unidade 4 vamos aprender como escrever e usar uma instrução para efetuar representações gráficas em Python. Iremos, também, aprender a como traçar um gráfico e configurar a representação.
Objetivos:
- Explorar o módulo TI PlotLib.
- Representar um ponto e um segmento de reta.
- Configurar uma representação gráfica
Passo 1
Etapa 1: A livraria ou módulo TI PlotLib
Para efetuar uma representação gráfica recorrendo a um programa teremos que fazer com que o programa “reconheça” as instruções de representação gráfica. Assim, teremos que, antes do uso dessas instruções, “embutir” as funções de representação gráfica de uma biblioteca TI PlotLib.
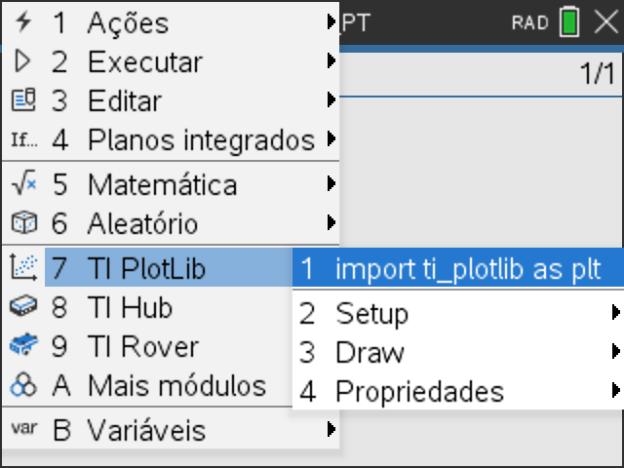
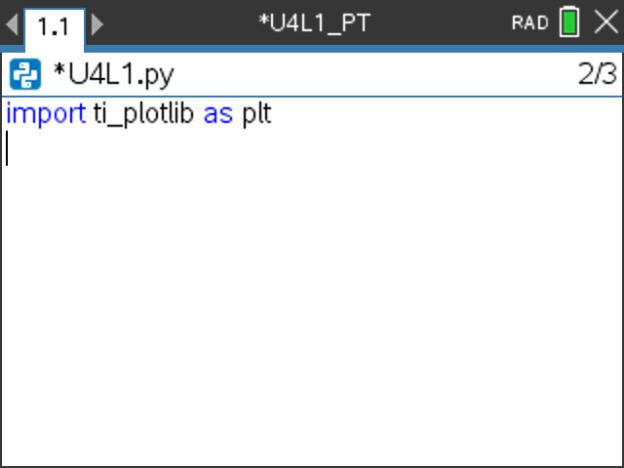
Abra um novo documento TI-Nspire com um novo programa da aplicação TI-Python e designe-o por U4L1, colocando como primeira instrução a inclusão do módulo TI PLotLib (tecla ![]() , escolher a opção 7: TI PlotLib e depois 1: import ti_plotlib as plt.
, escolher a opção 7: TI PlotLib e depois 1: import ti_plotlib as plt.
Passo 2
Desta forma, a partir desta instrução, o programa reconhecerá as habituais instruções usada na representação gráfica.
Numa primeira fase, vamos escrever um programa que permita representar um ponto conhecidas as suas coordenadas. De seguida, alteraremos o programa de modo a localizar o ponto no referencial e a alterar a sua cor.
Para terminar esta primeira lição, colocaremos visível o nome de cada eixo e daremos um título à representação gráfica.
Passo 3
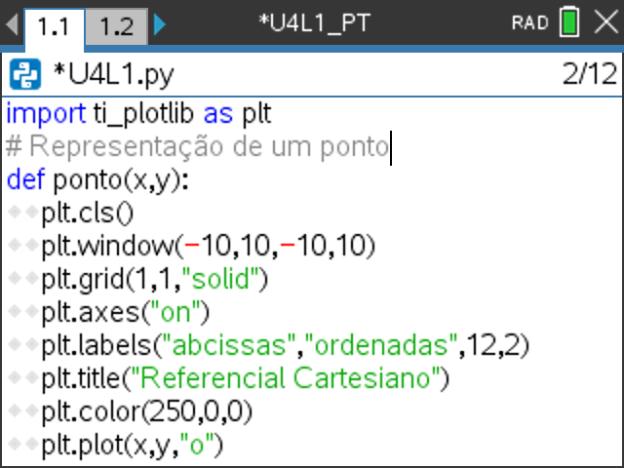
Defina uma função que tenha como argumentos as coordenadas de um ponto e, em seguida, efetue a representação gráfica desse ponto.
- Comecemos por limpar do ecrã a representação gráfica usando a função pl.cls(), que encontrará no módulo TI PlotLib (tecla
 , opção 7: TI PlotLib, depois opção 2:Configurar e por fim 1:cls()) .
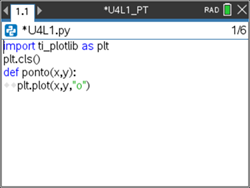
, opção 7: TI PlotLib, depois opção 2:Configurar e por fim 1:cls()) . - De seguida defina uma função, designe-a por ponto(), recorrendo ao menu 4: Planos integrados e à opção 1: Funções. Coloque como argumentos as variáveis x e y, coordenadas no plano.
- Para representar um ponto, selecione no submenu 3: Desenhar a opção 6: plot(x,y,"mark"), situado no menu do módulo TI PlotLib.
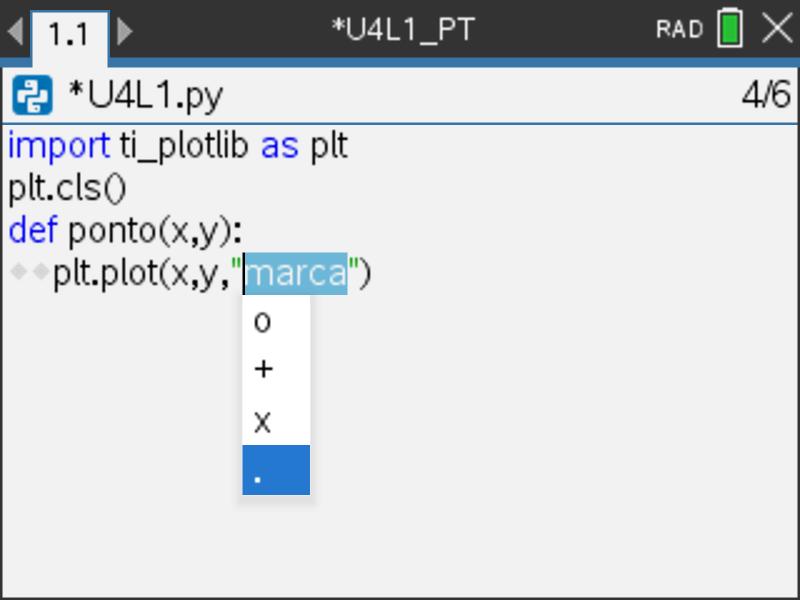
- Escolha, agora, a marca que pretende para representar o ponto.
Passo 4
SUGESTÃO:
A marca utilizada para a representação do ponto dever ser escolhida tendo em atenção o número de pontos e outros elementos a representar na mesma janela, sendo aconselhado, pelo menos no caso de serem muitos pontos, a optar-se pela forma de pixel (.). Após a escolha da forma da marca, para a alterar terá que a inserir de novo através do menu respetivo.
Passo 5
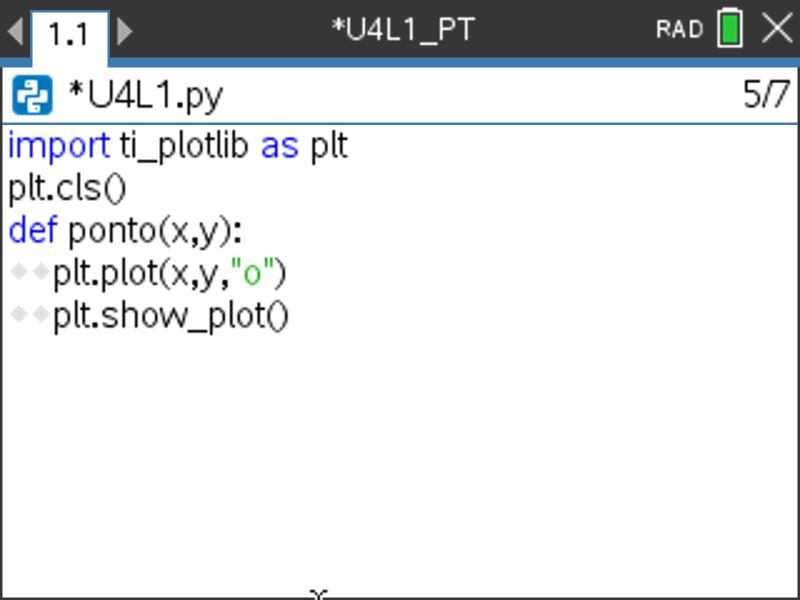
- Termine o programa efetuando a representação gráfica, usando a função show_plot() (opção 3: shown_plot() do submenu 3: Desenhar do módulo TI PlotLib).
- Execute o programa, clicando simultaneamente nas teclas
 e R, e de seguida, no interpretador, clique na tecla
e R, e de seguida, no interpretador, clique na tecla  e selecione a função ponto(). Poderá, também, escrever o nome da função que o interpretador reconhecerá.
e selecione a função ponto(). Poderá, também, escrever o nome da função que o interpretador reconhecerá. - Coloque as coordenadas do ponto que pretende representar, os dois argumentos da função, e execute a função clicando na tecla
 . Observe o ecrã.
. Observe o ecrã.
Passo 6
- Para sair da representação gráfica pode clicar na tecla
 ou na tecla
ou na tecla  , uma primeira vez para terminar a representação e uma segunda vez para voltar ao interpretador (Shell).
, uma primeira vez para terminar a representação e uma segunda vez para voltar ao interpretador (Shell). - Execute novamente a função ponto, agora com outras coordenadas (por exemplo ponto(10,10), ponto(-4,6), …) e observe o ecrã com a representação gráfica do ponto. Constatará que para algumas coordenadas o ponto não surge visível no ecrã. Teste, usando esta função, a janela de visualização assumida por defeito.
Passo 7
OBSERVAÇÃO:
Ao escrever um programa usando as instruções para obter uma representação gráfica, será necessário especificar os parâmetros da janela de visualização, assim como, eventualmente, tornar visível um sistema de eixos, o nome dos eixos, uma grelha de fundo, etc.
Passo 8
Etapa 2: Melhorar a representação gráfica
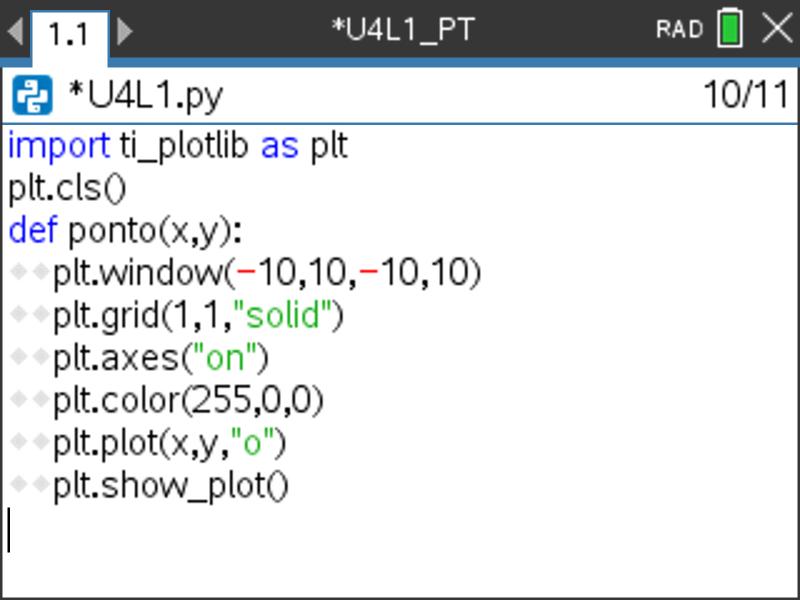
Insira a função plt.cls() antes da definição da função, para evitar que outros elementos fiquem sobrepostos à representação gráfica.
A partir das diferentes opções do submenu de configurações do módulo TI PlotLlib, adicione ao seu programas as instruções seguintes que lhe permitam:
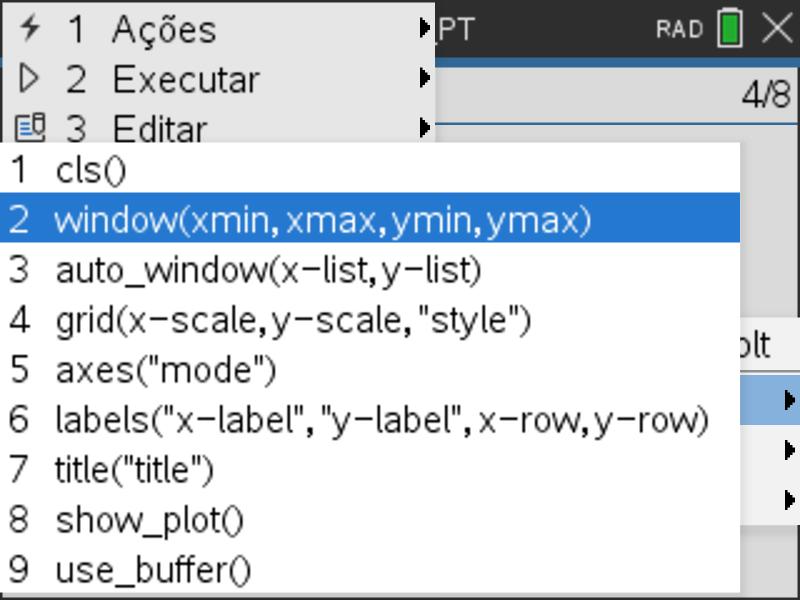
- definir uma janela gráfica com as seguintes caraterísticas: Xmin = -10; Xmax = 10; Ymin = -10 e Ymax = 10 (submenu 2: Configurar seguido de opção 2: window(xmin,xmax,ymin,ymax)).
Passo 9
- exibir uma grelha (submenu 2: Configurar seguido de opção 4: grade 4), sendo que o tipo de grelha é deixado à sua escolha.
- exibir os eixos coordenados (opção 5: axes(“mode”)).
- alterar a cor do ponto (menu 3: Desenhar, a seguir 1: color(vermelho,verde,azul)).
Passo 10
OBSERVAÇÕES:
- Para cortar, copiar ou colar uma linha, use os atalhos Ctrl + X , Ctrl + C e Ctrl + V, respetivamente.
- A cor de um ponto ou de uma linha deve ser definida pelos parâmetros da mistura de cores RGB (red-vermelho, green-verde, blue-azul), cada parâmetro pode assumir um valor no intervalo [0; 255]. As cores são codificadas em 8 bits, ou seja, 28 = 256 possibilidades, incluindo o 0 que corresponde a ausência da cor, por exemplo RGB(255, 0, 0) corresponde ao vermelho “puro” já que está ausente o verde e o azul.
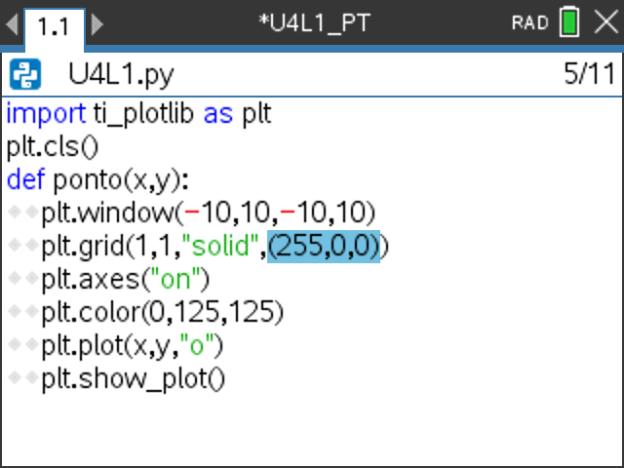
- Também é possível desenhar a grelha de fundo com cores, completando para tal a instrução grid da seguinte forma: grid(x-scale, y-scale,“style",(r,g,b)). Veja-se o exemplo de formatação usada no programa ao lado e a imagem de execução da função ponto().
Passo 11
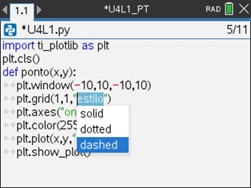
DICA:
Utilize a tecla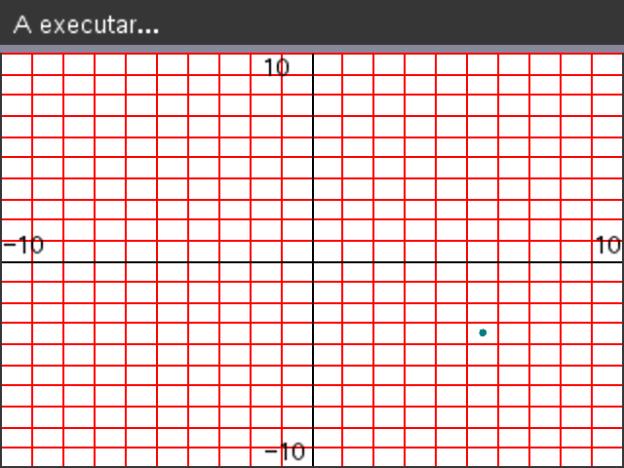
Passo 12
Voltemos ao nosso programa melhorado, sem formatações extra.
- Execute o programa, atalho
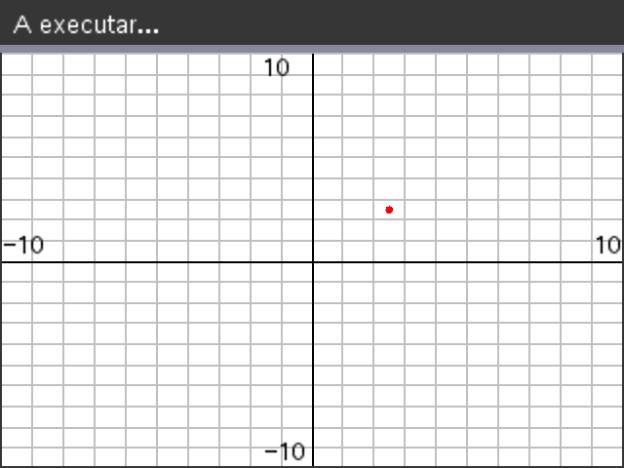
 , e já na página do interpretador, escreva a função ponto() e execute-a clicando na tecla
, e já na página do interpretador, escreva a função ponto() e execute-a clicando na tecla 
- Deverá obter um ecrã idêntico ao que se encontra ao lado.
Passo 13
OBSERVAÇÃO:
Como no programa a função cls() se encontra fora da função ponto(), ao executar o programa de imediato é executada a função cls() e por isso surge uma janela de desenho vazia, sendo necessário premir duas vezes a tecla ![]() para voltar ao interpretador, e aí executar a função ponto(). Esta situação resolve-se colocando a função cls() dentro e no início da função ponto(), experimente.
para voltar ao interpretador, e aí executar a função ponto(). Esta situação resolve-se colocando a função cls() dentro e no início da função ponto(), experimente.
Passo 14
ATENÇÃO:
- Ao executar um programa,
 o interpretador é reiniciado, o que significa que se perde o histórico do interpretador, como por exemplo variáveis definidas anteriormente no interpretador ou até bibliotecas que haviam sido “embutidas” no interpretador (por exemplo outros programas).
o interpretador é reiniciado, o que significa que se perde o histórico do interpretador, como por exemplo variáveis definidas anteriormente no interpretador ou até bibliotecas que haviam sido “embutidas” no interpretador (por exemplo outros programas). - Note ainda que, ao guardar o programa, atalho
 , sem o executar a partir do editor, as alterações não são consideradas no interpretador, para tal sempre que alterar o programa tem que o executar novamente a partir do editor.
, sem o executar a partir do editor, as alterações não são consideradas no interpretador, para tal sempre que alterar o programa tem que o executar novamente a partir do editor.
Passo 15
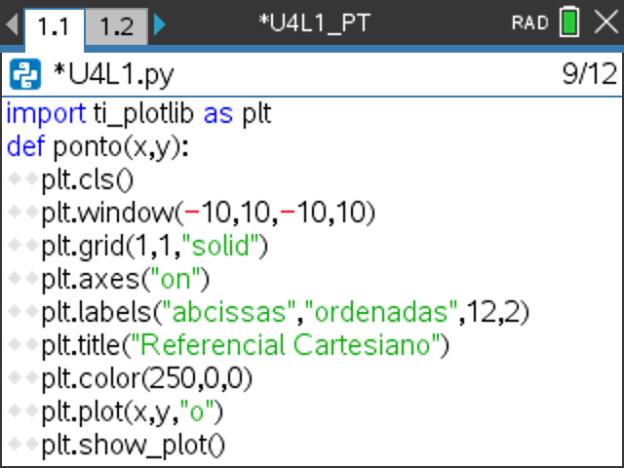
Altere novamente o programa de forma a colocar legendas nos eixos do referencial, por exemplo, “abcissa” e “ordenada”.
Para isso, inclua no seu programa (dentro da função, independentemente da localização) uma linha com a instrução plt.labels. Acede a esta função na opção 7: labels() do submenu 2: Configurar do módulo 7: TI PlotLib.
Vamos, ainda, adicionar um título à nossa representação gráfica, usando para tal a função plt.title, inserindo a função 7: title(“title”), do submenu 2: Configurar do módulo 7: TI PlotLib.
Passo 16
OBSERVAÇÕES:
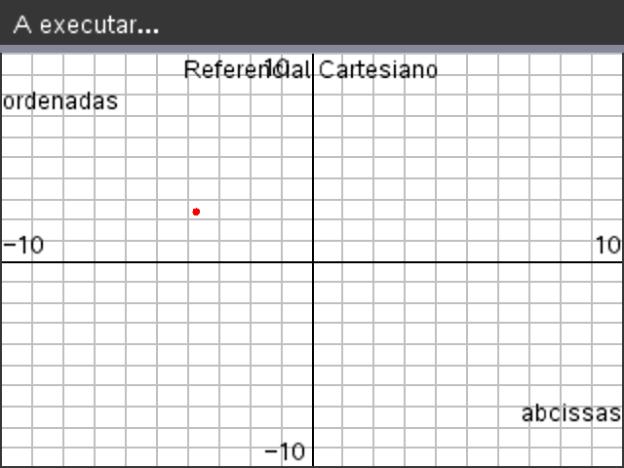
A função de labels("Etiqueta-x","etiqueta-y",x-row,y-row) permite designar os eixos coordenados, colocando as etiquetas na linha x e coluna y, que por defeito são a linha 12 para x e a coluna 2 para y, respetivamente justificado à esquerda e à direita.
- Execute novamente o programa, atalho
 , e na página do interpretador, execute a função ponto(-3.7,2.4) .
, e na página do interpretador, execute a função ponto(-3.7,2.4) . - Deverá obter um ecrã idêntico ao que se encontra ao lado.
RECORDE QUE:
Os carateres especiais (acentuados e outros) podem ser obtidos de duas formas: pressionando sucessivamente a tecla ![]() após inserir a letra ou procurando na tabela do código ASCI, usando o atalho
após inserir a letra ou procurando na tabela do código ASCI, usando o atalho ![]() +
+![]() , o carater pretendido. No software bastará utilizar, como habitual, o teclado do computador.
, o carater pretendido. No software bastará utilizar, como habitual, o teclado do computador.
Passo 17
MAIS ALÉM:
Faça um upgrade ao seu programa, construa uma nova função que lhe permita representar graficamente um segmento de reta dadas as coordenadas dos seus extremos.
- Comecemos por colocar uma linha de comentário (atalho
 +
+  ), antes de cada uma das funções do programa, para desta forma qualquer utilizador saber facilmente o objetivo da função.
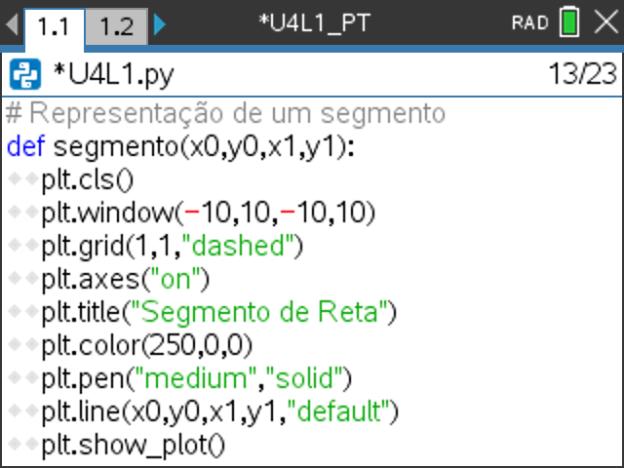
), antes de cada uma das funções do programa, para desta forma qualquer utilizador saber facilmente o objetivo da função. - Deseguida construa a função segmento() tendo em atenção as instruções essenciais constantes na imagem ao lado. Poderá, se entender, alterar algumas das configurações/parâmetros definidos.
- Para representar o segmento de reta iremos utilizar a função plt.pen(), acessível através do menu 3: Desenhar (opção 9: pen ("size", "style"), que permite configurar a largura e o estilo da linha.)
Passo 18
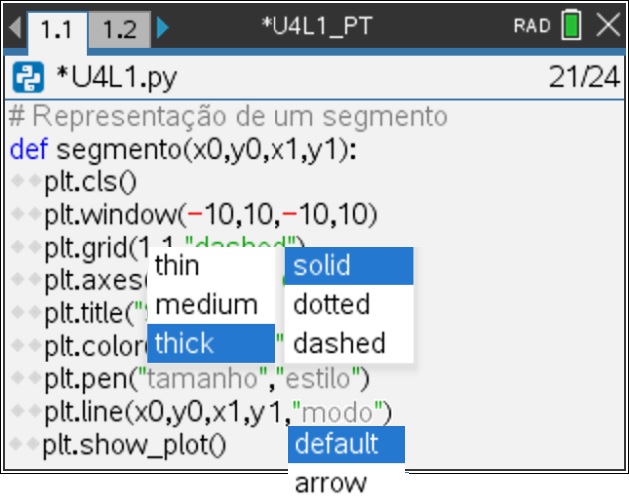
OBSERVAÇÃO:
Para configurar as funções plt.pen() e line(), a primeira com os campos relativos ao tamanho (estreito, médio, largo) e ao estilo (sólido, ponteado, tracejado) e a segunda com o campo relativo ao modo (por feito, setas), surge uma janela de escolha de opção conforme imagem ao lado. Note que a imagem é uma composição de captura de ecrãs, não sendo possível obter como um único ecrã.
Passo 19
RECORDE QUE:
A captura de ecrã no software pode ser obtida através do atalho ![]() + J, ou usando a ferramenta
+ J, ou usando a ferramenta ![]()
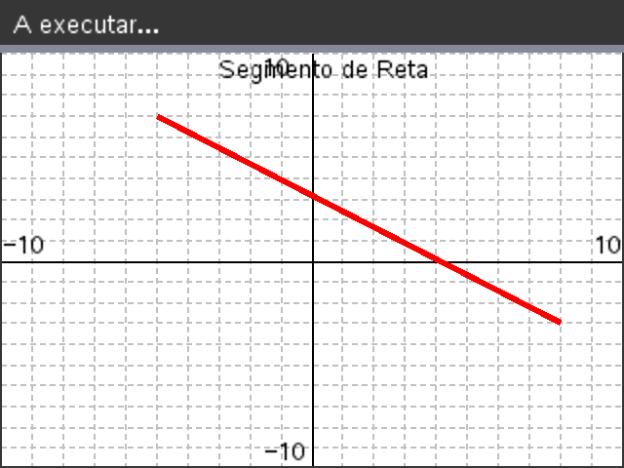
- Por fim, execute mais uma vez o programa, atalho
 , e na página do interpretador, execute a função segmento(-5,7,8,-3) .
, e na página do interpretador, execute a função segmento(-5,7,8,-3) . - Obterá um ecrã idêntico ao que se encontra ao lado.
Passo 20
ATENÇÃO:
Após executar, no interpretador, qualquer uma das funções definidas no programa a cor que fica definida para desenho é a vermelha (cor escolhida para o ponto e o segmento de reta), por isso se executarmos de seguida qualquer uma das funções todo os elementos representados terão essa cor. Assim, será indicado no início de cada função definir a cor por defeito como sendo o preto, RGB(0,0,0).Lição 2: Representar graficamente uma função
Descarregar documentos do professor / alunoNesta segunda lição da Unidade 4 vamos aprender como representar graficamente uma função utilizando a biblioteca TI PlotLib da aplicação TI-Python
Objetivos:
- Representar graficamente uma função.
- Revisitar o conceito de ciclo fechado.
- Configurar uma representação gráfica.
Passo 1
Propomos, nesta lição, a criação de um programa na aplicação TI-Python utilizando a biblioteca TI PlotLib que permite desenhar a representação gráfica de uma função para certos valores do objeto x pertencentes a um intervalo [a; b] com N segmentos.
O programa que irá criar será muito geral para que possa ser reutilizado em outros exemplos.
Passo 2
OBSERVAÇÃO:
Se os conceitos de ciclo e funções em Python não lhe são familiares, é aconselhável ir realizar as lições das unidades 1, 2 e 3 do TI-Código Python dos “10 Minutos de Código”.
- Comecemos por abrir um novo documento e adicionar uma página com a aplicação TI-Python, criando um novo programa designando-o por U4L2.
- Importe, no início do programa, o módulo TI PlotLib, que se obtém clicando na tecla
 e depois escolhendo a opção 7: TI PlotLib.
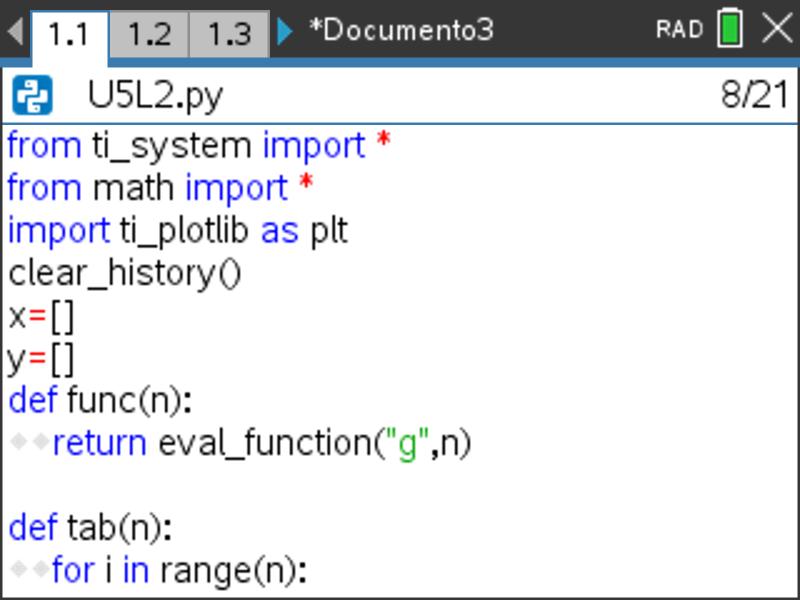
e depois escolhendo a opção 7: TI PlotLib. - Crie, de seguida, a função quadrática definida por g(x) = x2 – 3x + 4.
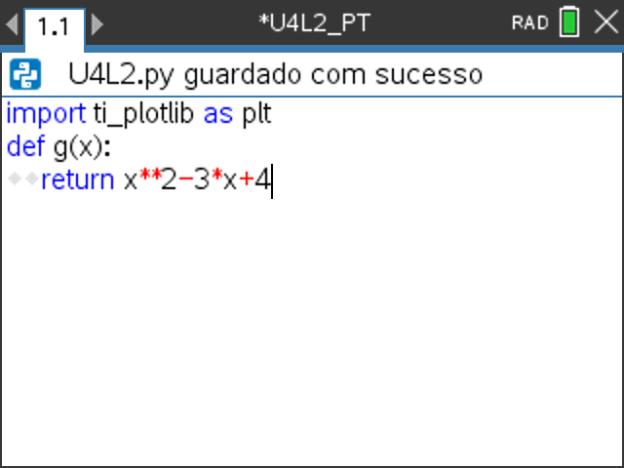
Passo 3
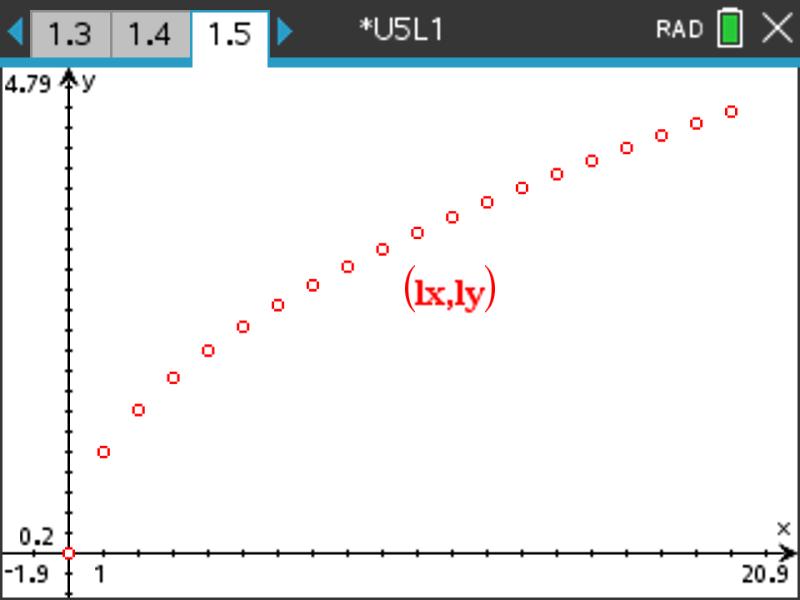
SUGESTÃO:
A lista das abcissas, que designaremos por lx, será construída utilizando um ciclo limitado cuja instrução for i index in range(size) poderá ser obtida clicando na tecla ![]() , depois selecionar opção 4: Planos integrados e por fim 2: Controlo. Já a lista das ordenadas, ly, obter-se-á a partir das imagens dos elementos da lista das abcissas, lx, portanto utilizaremos a opção 7: for index in list do mesmo menu anterior.
, depois selecionar opção 4: Planos integrados e por fim 2: Controlo. Já a lista das ordenadas, ly, obter-se-á a partir das imagens dos elementos da lista das abcissas, lx, portanto utilizaremos a opção 7: for index in list do mesmo menu anterior.
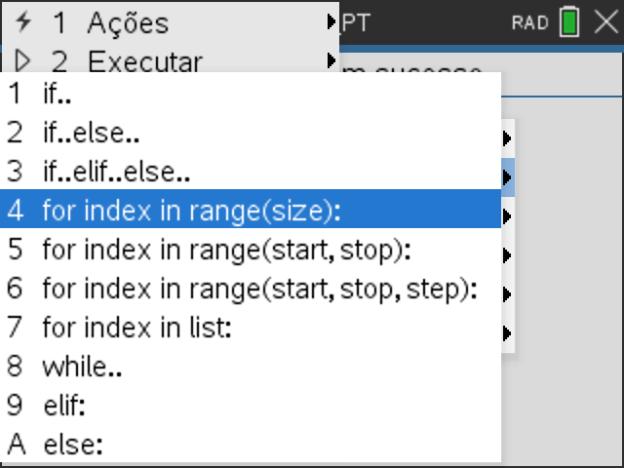
Passo 4
DICA:
Insira um novo problema no seu documento e experimente esta forma de gerar uma lista de valores a partir de uma página do interpretador do TI-Python. Veja a imagem ao lado e faça a interpretação da estratégia usada.
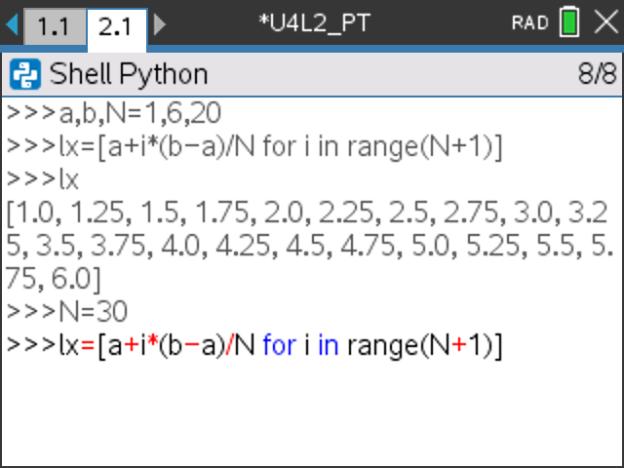
Passo 5
Agora, estará pronto para obter uma representação gráfica da função g. Assim, insira sucessivamente as seguintes instruções no programa, tendo como objetivo efetuar o indicado em cada uma delas:
- Limpar o ecrã: plt.cls() .
- Ajustar os parâmetros da janela de visualização gráfica: plt.window(xmin, xmax, ymin, ymax).
- Mostrar os eixos coordenados: plt.axes("on").
- Colocar legenda nos eixos coordenados: plt.labels(“x”, “y”).
- Executar a representação gráfica: plt.plot(lx, ly,"+").
- Mostrar a representação gráfica: plt.show_plot().
Todas essas instruções estão no módulo TI PlotLib, sendo que os parâmetros de configuração da representação gráfica se encontram no submenu 2: Configurar e as instruções de representação gráfica no submenu 3: Desenhar.
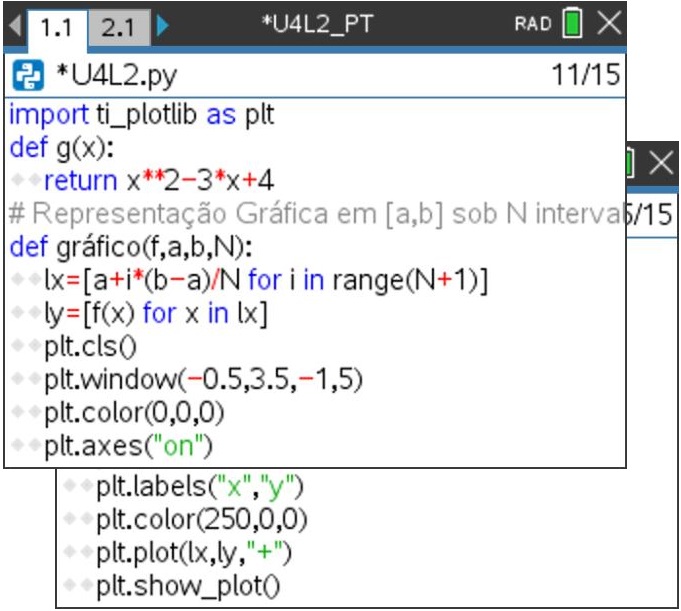
Passo 6
NOTE QUE:
As instruções para a escolha da cor em RGB (vermelho, verde, azul) devem ser parametrizados entre 0 e 255 e inseridas no programa com localização criteriosa, de forma a evitar, por exemplo, que os eixos sejam vermelhos.
- Execute o programa, atalho
 , e na página do interpretador insira a função gráfico() clicando, por exemplo, na tecla
, e na página do interpretador insira a função gráfico() clicando, por exemplo, na tecla  .
. - Obtenha a representação gráfica da função g, no intervalo [0, 3] e com a divisão em 25 subintervalos.
- Obterá a representação que se encontra na imagem ao lado.
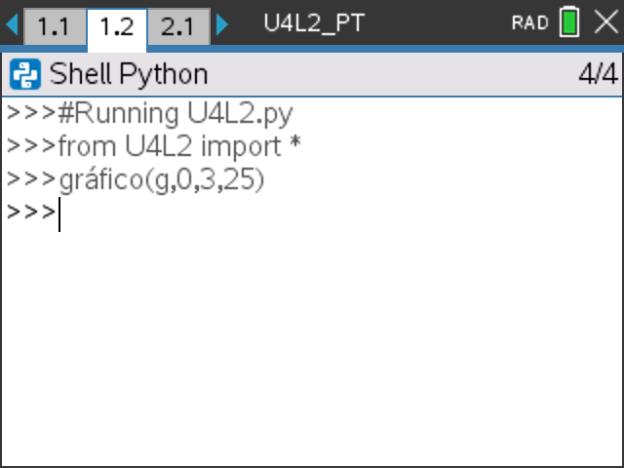
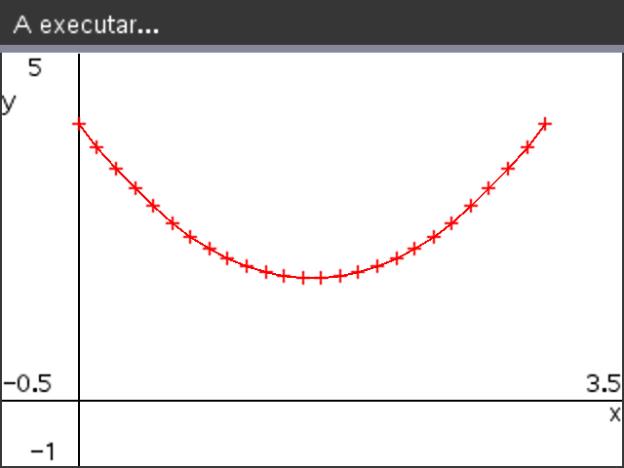
Passo 7
SUGESTÃO:
Se optar por uma partição do intervalo num grande número de subintervalos, e consequentemente a representação ser obtida através de um grande número de pequenos segmentos, então deve optar pela marca da representação ser em pixel (×) (em vez de +).
Passo 8
MAIS ALÉM:
Poderá alterar ou utilizador o programa para ir mais além na representação e estudo de funções, por exemplo:
- Mostrar a grelha de fundo no referencial.
- Alterar a função e/ou estudar várias funções
- Realizar um estudo matemático (cálculo diferencial), por exemplo, representando a função com 6 segmentos e depois 50.
Lição 3: Representar graficamente uma função
Descarregar documentos do professor / alunoNesta terceira lição da Unidade 4 vamos aprender como representar graficamente um conjunto de dados e, de seguida, procurar o modelo matemático que melhor se ajusta à nuvem de pontos
Objetivos:
- Representar graficamente uma nuvem de pontos.
- Procurar e utilizar um modelo de regressão.
- Utilizar listas em TI-Python.
Passo 1
PROBLEMA:
Durante uma enchente, a fim de fornecer informações práticas à população, as autoridades registaram, a cada hora desde o início da enchente, o nível máximo de água em relação a um ponto de referência.
Os dados registados encontram-se na tabela abaixo.
| T(h) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| H(cm) | 130 | 127 | 123 | 118 | 116 | 111 | 105 | 103 | 101 | 95 | 86 | 80 | 71 |
Pretende-se representar a nuvem de pontos usando a biblioteca TI PlotLib, para depois procurar um modelo matemático que permita fazer uma extrapolação, a fim de prever o tempo total da recessão.

Passo 2
IMPLEMENTAÇÃO:
Num novo documento adicione uma página com o editor de programa em TI-Python, designe-o por U4L3.
- Comece por importar o módulo TI PlotLib, opção 7: TI PlotLib do menu do TI-Python.
- Guarde os dados do problema em duas novas listas, lt e lh para, respetivamente lista dos tempos e lista das alturas.
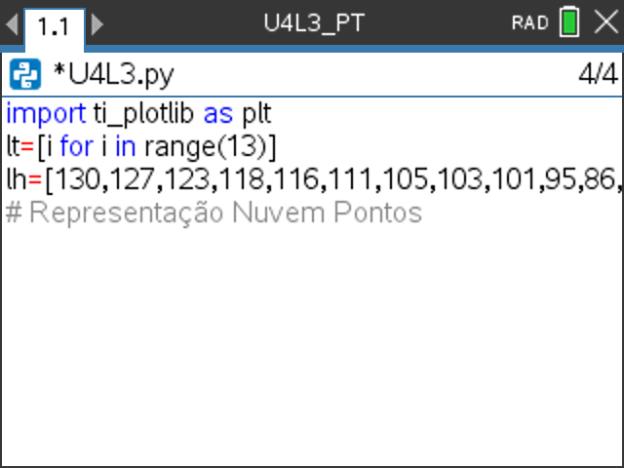
Passo 3
RECORDE QUE:
Na linguagem Python uma lista é representada através de parênteses retos colocando os elementos das listas entre os parênteses e separados por virgulas.
- Prepare de seguida a representação gráfica da nuvem de pontos:
- Limpar o ecrã: plt.cls()
- Definir a janela de visualização: xmin= – 2; xmax=20; ymin= – 20, ymax=200 escrevendo plt.window(–2,20, –2,200).
- Mostrar os eixos coordenados: plt.axes().
- Mostrar a representação gráfica sob a forma de nuvem de pontos: plt.scatter(). (Acessível pelo submenu 7: TI PlotLib, seguida da opção 3: Desenhar e por fim a opção 4: plt.scatter(x-list,y-list,”mark”) .
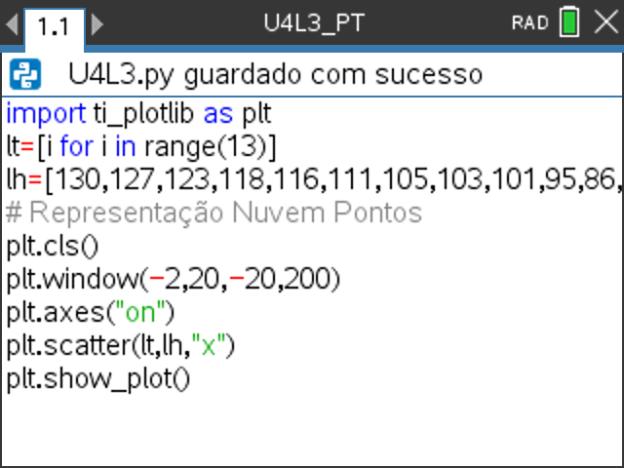
Passo 4
Todas essas instruções estão no módulo TI PlotLib, sendo que os parâmetros de configuração da representação gráfica se encontram no submenu 2: Configurar e as instruções de representação gráfica no submenu 3: Desenhar.
Execute o programa, atalho ![]() , e observe a representação gráfica.
, e observe a representação gráfica.
Se tudo estiver correto, deverá obter um ecrã igual ao do lado.
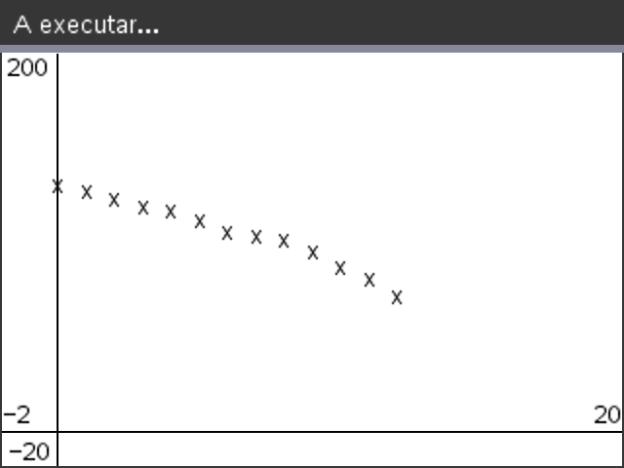
Passo 5
Os pontos estão todos alinhados? Que curva se ajustará melhor à nuvem?
Vamos então, agora, encontrar o modelo matemático, função afim, que melhor passa por todos os pontos da nuvem.
Para isso, deve adicionar uma linha de código ao seu programa com a instrução plt.lin_reg(x-list, y-list, "display") para que a expressão da reta de regressão seja calculada a partir das listas de dados lt e lh, depois representada e exibida centralizada.
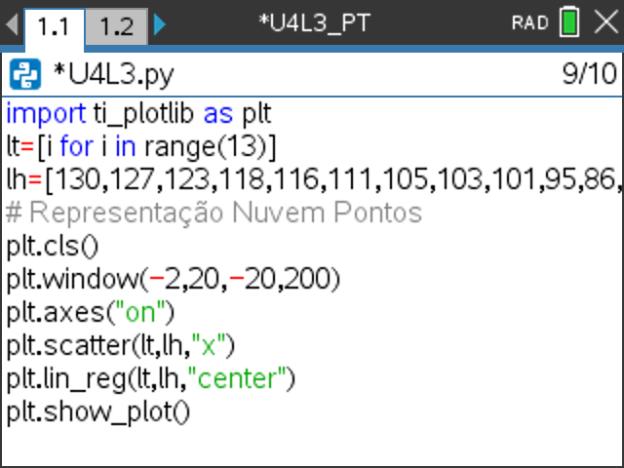
Passo 6
Mais uma vez, acede-se à função plt.lin_reg() através do módulo TI PlotLib, no submenu 3: Desenhar, seguido da opção 8: plt.lin_reg(x-list, y-list, "display").
Para saber o tempo de recessão total, ainda precisa resolver a equação do primeiro grau:
- 4.64 x + 132.90 = 0
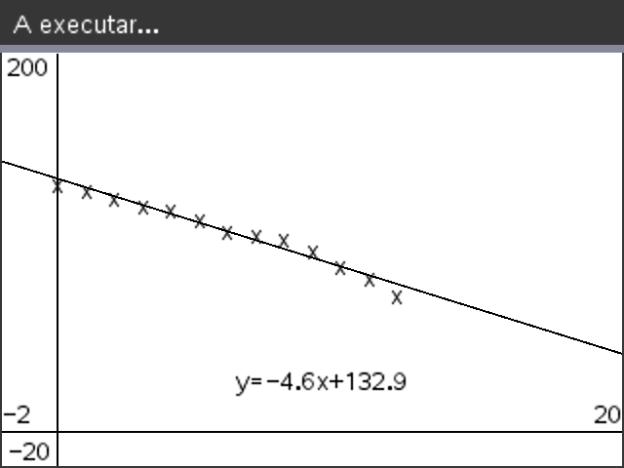
Passo 7
Dar cor à representação gráfica:
Usando a função que permite definir a cor dos elementos representados, plt.color(), vamos:
- manter os eixos coordenados a preto: plt.color(0,0,0) ;
- a representação gráfica da nuvem de pontos a vermelho: plt.color (255,0,0) ;
- a representação da reta de regressão a azul: plt.color(0,0,255).
Será também interessante colocar um título e etiquetas nos eixos!
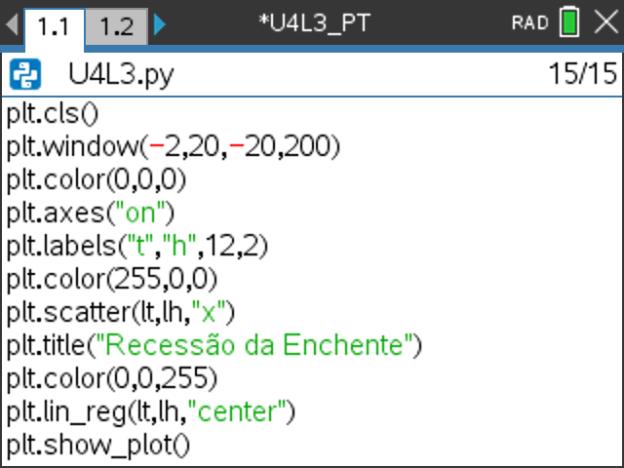
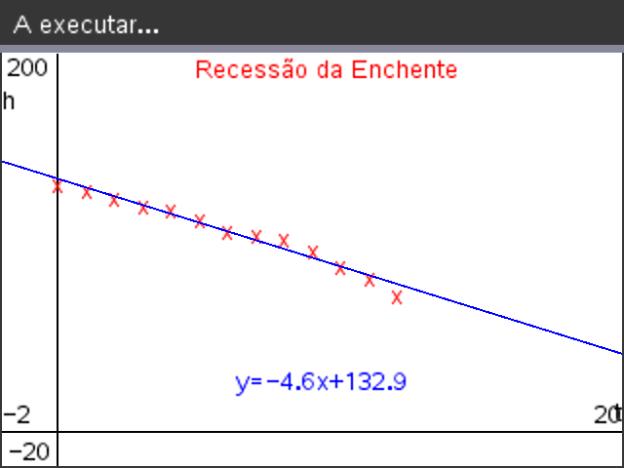
Passo 8
SUGESTÕES:
Para evitar problemas de sobreposição de elementos, opte por nomes curtos para as etiquetas dos eixos, por exemplo “t” e “h”. Utilize a instrução plt.labels("x-label", "y-label" ", x, y), onde x e y representam a linha as etiquetas são escritas. Por defeito, essas linhas são respetivamente 12 e 2 para x e y e, respetivamente, justificadas à esquerda e à direita.
Da mesma forma, a equação da reta de regressão pode ser exibida no local desejado, usando a instrução lin_reg (x-list, y-list, "display", linha), sendo por defeito a linha 11.
Aplicação: Posições sucessivas num movimento
Descarregar documentos do professor / alunoNesta aplicação da Unidade 4 vamos aprender como estudar um movimento a partir das medições efetuadas por um cronofotógrafo e revisitar o conhecimento adquirido, nas três lições anteriores, na utilização da biblioteca TI PlotLib.
Objetivos :
- Representar uma nuvem de pontos.
- Efetuar o cálculo, seguido da representação dos vetores de um sistema modelado por um ponto.
Passo 1
PROBLEMA:
Estudemos o movimento de uma bola de golfe a partir de uma cronofotografia ou fotografia estroboscópica (registo do movimento de um objeto tirando fotos num intervalo de tempo fixo, observando a sua posição).
Pretende-se representar a evolução do vetor velocidade ao longo do tempo.
As posições são lidas a cada 0,066 segundos e registadas numa tabela.
| t(s) | 0 | 0.066 | 0.132 | 0.198 | 0.264 | 0.33 | 0.396 | 0.462 | 0.528 | 0.594 | 0.66 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| x(m) | 0.01 | 0.25 | 0.57 | 0.91 | 1.22 | 1.54 | 1.87 | 2.16 | 2.49 | 2.81 | 3.15 |
| y(m) | 0.015 | 0.34 | 0.681 | 1.01 | 1.297 | 1.559 | 1.768 | 1.95 | 2.08 | 2.158 | 2.193 |
NOTA:
Na Unidade 5, deste projeto “10 Minutos de Código”, poderá aprender a importar dados de listas da calculadora utilizando o módulo TI System.
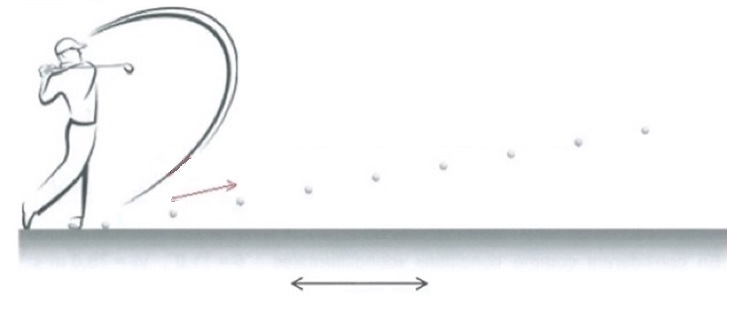
Passo 2
IMPLEMENTAÇÃO:
Etapa 1: Introdução das medidas registadas e criação da lista com os valores dos tempos de registo.
- Adicionar um novo programa TI-Python com o nome U4AP.
- Importar a biblioteca TI PlotLib para se utilizar as instruções de representação gráfica.
- Definir a variação do tempo de registo de dados, dt=0.066.
- Inserir as medidas correspondentes às coordenadas, x e y, dos pontos identificados durante a análise da cronofotografia.
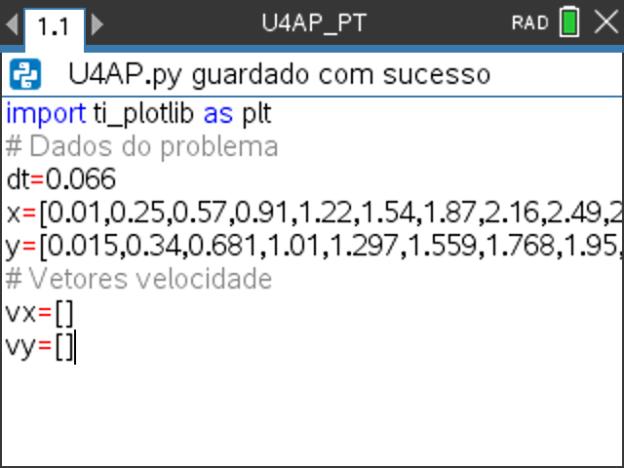
Passo 3
Etapa 2: Cálculo dos vetores velocidade
- O vetor velocidade, num dado instante ti, é dado pela igualdade:
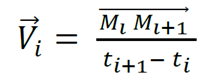 sendo Mi a posição da bola no instante ti.
sendo Mi a posição da bola no instante ti. - Desta forma, portanto, não será representado o vetor velocidade do último ponto da lista, facto que dever-se-á ter em atenção no código.
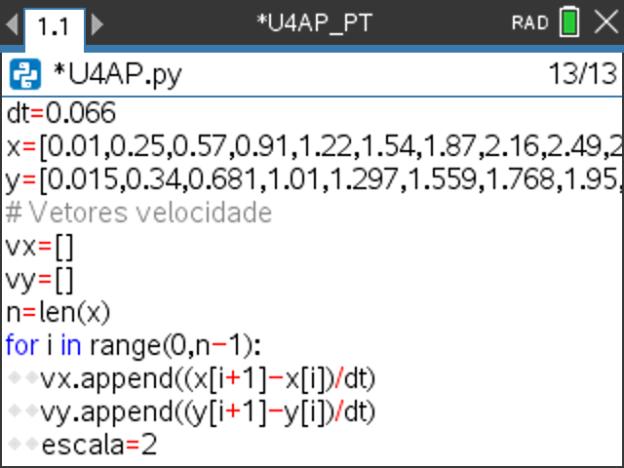
Passo 4
DICA:
Para tornar a representação gráfica legível, usaremos 2 como fator de escala.
RECORDE QUE:
- A função len(x) permite obter o número de elementos da lista x, isto é, a sua dimensão (comprimento). Poderá escrever diretamente no programa o nome da função ou aceder ao menu 4: Planos integrados, seguido de 4: Listas e por fim 3: len().
- A instrução .append() permite acrescentar, no fim da lista, um elemento a uma dada lista e que se pode obter no menu 4: Planos integrados, seguido de 4: Listas e por fim 6: append().
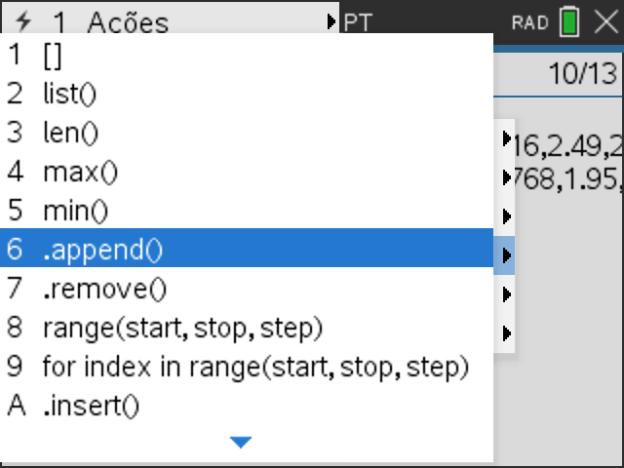
Passo 5
Etapa 3: Definição dos parâmetros da representação gráfica
- plt.cls() – para limpar o ecrã.
- plt.title(“title”) – para inserir um título no gráfico (“Velocidades Bola Ténis”).
- plt.window(xmin, xmax, ymin, ymax) – para definir a janela de visualização da representação gráfica ([–0.5,3.5] x [–1, 3]).
- plt.grid(x-scale, y-scale, “type”) – para mostrar uma grelha de fundo com linha contínua e graduação 0.5 ((0.5, 0.5,”solid”)).
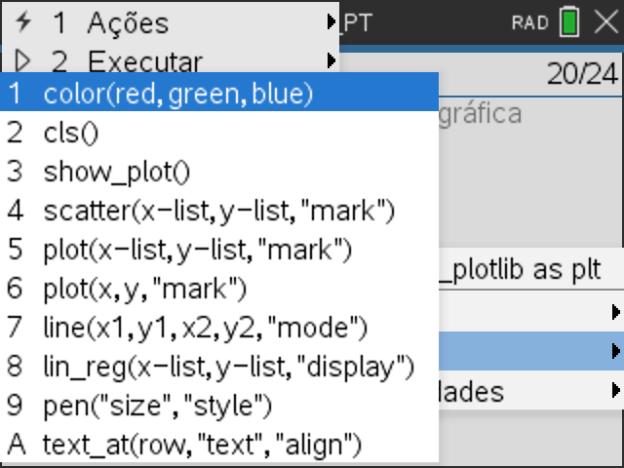
Passo 6
- plt.color(255,0,255) – para definir a cor magenta para a nuvem de pontos
- plt.scatter(x-list, y-list, “mark”) – para definir as listas e a marca da nuvem de pontos ( (x,y,”o”) ).
- plt.color(0,0,0) – para definir como preto da cor dos eixos coordenados.
- plt.pen(“size”, “style”) – para definir os eixos com espessura média e linha contínua (“medium”,”solid”).
- plt.labels(“x-label”, “y-label”) – para definir as etiquetas dos eixos coordenados, localizadas por defeito nas linhas 12 e 2, respetivamente (“x(m)”,”y(m)”).
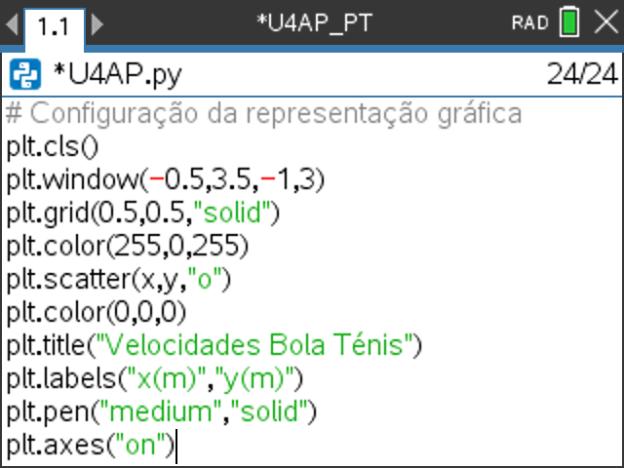
Passo 7
A representação gráfica dos vetores velocidade é efetuada através de um ciclo limitado de n-1 valores, com as instruções:
- plt.pen(“size”, “style”) – para traçar os vetores com espessura estreita e linha contínua (“thin”,”solid”).
- plt.line(x0,y0,x1,y1) – para traçar um vetor velocidade.
No fim do ciclo, é necessário tornar visível todos os elementos gráficos através da função:
- plt.show() – para mostrar toda a representação gráfica.
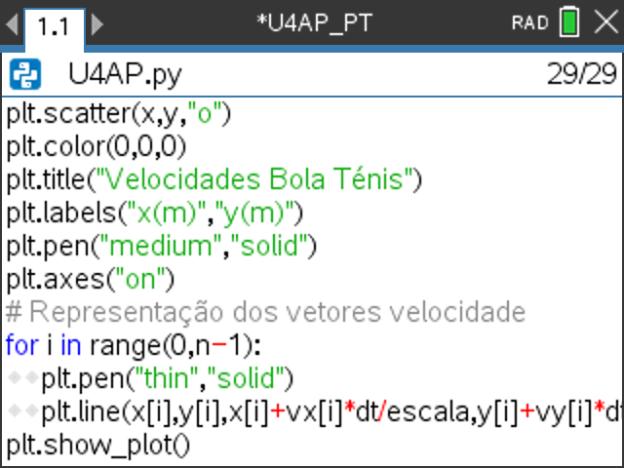
Passo 8
RECORDE QUE:
A posição da bola de ténis num instante t, entre os instantes ti e ti + 1, pode ser identificada num referencial cartesiano por xi + vxi × dt para a abcissa e yi + vyi × dt para a ordenada, com dt=t – ti. Note que, se o instante t for igual a ti + 1, então a posição da bola tem as coordenadas (xi + 1 , yi + 1), já que dt= ti + 1 – ti =0.066 .
- Execute o programa, clicando simultaneamente nas teclas
 e
e  .
. - Deverá obter uma representação análoga à do ecrã ao lado. Observe a representação e associe cada linha de código aos elementos representados.
NOTE QUE:
O facto escala utilizado no programa, no caso de 2, permite representar um vetor colinear com o vetor velocidade e tornar a representação mais percetível.
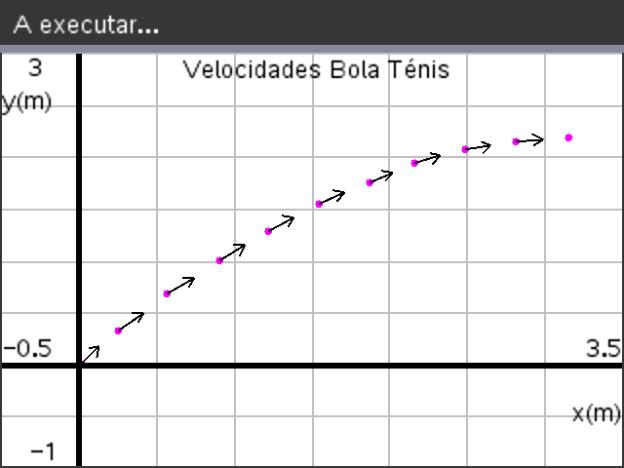
Passo 9
OBSERVAÇÕES:
Para cortar, copiar ou colar uma linha ou uma instrução, use os atalhos Ctrl + X , Ctrl + C e Ctrl + V, respetivamente.
Para programas mais complexos e/ou mais extensos, poderá optar por duplicar o programa como estratégia de reutilização de trabalho realizado. Para isso, com o editor de programas do TI-Python aberto no programa a duplicar, pressione a tecla ![]() , em seguida na opção 1: Ações e por fim seleciona a opção 3: Criar cópia … . Surgirá uma janela para inserir o nome.
, em seguida na opção 1: Ações e por fim seleciona a opção 3: Criar cópia … . Surgirá uma janela para inserir o nome.
Se a quantidade de dados a utilizar for grande ou proveniente de uma atividade experimental realizada com uma consola de recolha de dados, é possível usar a aplicação "Listas e Folha de Cálculo" da TI-Nspire CX II para copiar dados facilmente e guardá-los em forma de listas antes de importá-los (consulte a Lição 1 da Unidade 5).
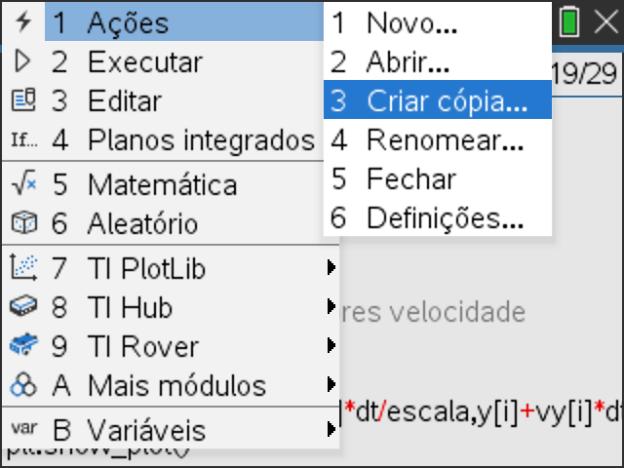
- Lição 1
- Lição 2
- Lição 3
- Aplicação
Unidade 5: Utilização da biblioteca TI System
Lição 1: Trabalhar com dados
Descarregar documentos do professor / alunoNesta primeira lição da Unidade 5, pode aprender como usar a biblioteca TI System para importar ou exportar listas num programa em Python.
Objetivos :
- Importar e exportar listas.
- Revisitar os conceitos da Unidade 4 sobre representações gráficas.
Passo 1
A biblioteca ou módulo TI System usada sozinha ou associada a outras, permite comunicação bidirecional com a calculadora gráfica.
Para carregar esta biblioteca, pressionar ![]() depois A Mais módulos e finalmente 3 TI System.
depois A Mais módulos e finalmente 3 TI System.
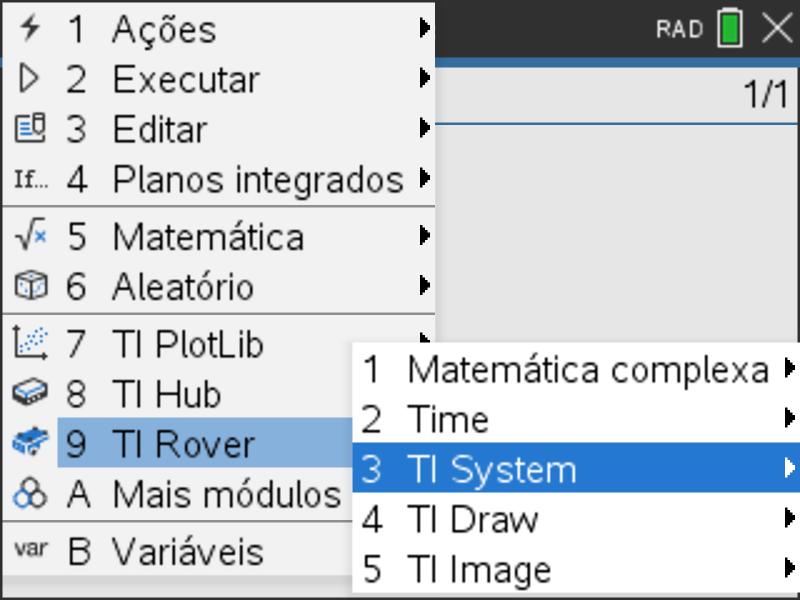
Passo 2
Nesta lição, vamos centrar a atenção sobre as instruções:
4: var=recall_list ("name" ) e 5: store_list ("name",list )
As outras opções desta biblioteca serão abordadas nas próximas lições.
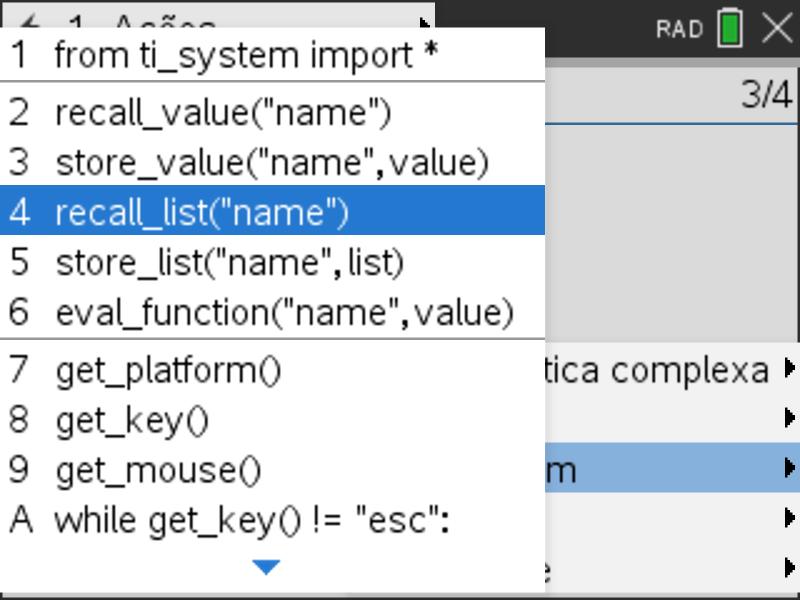
Passo 3
1: Importar dados da calculadora.
a). Construir duas listas.
Em primeiro lugar, vamos criar apenas duas listas contendo os dados.
- Crie uma nova página de calculadora

 depois escolha1 Adicionar Calculadora.
depois escolha1 Adicionar Calculadora. - O mesmo trabalho poderia ter sido realizado a partir da aplicaçãoListas e Folha de Cálculo.
Crie uma lista l1.com a sequência de números de 0 a 12, com passo de 0.2.
Passo 4
De seguida crie outra lista l2, das imagens de x (imagens dos dados da lista l1) pela função f definida por: x⟼-x2 /2 + 3x + 1
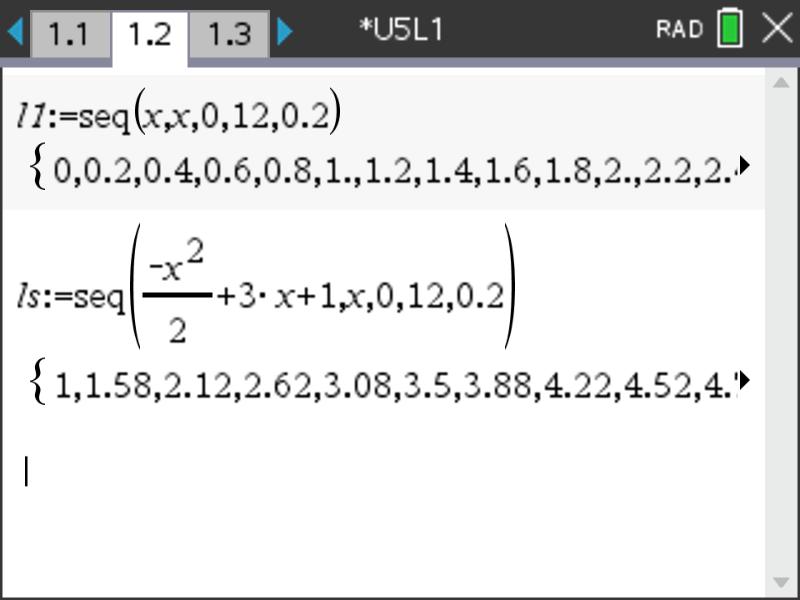
Passo 5
- Adicione uma nova página com a aplicação Gráficos.
- Obtenha nessa página a representação gráfica da nuvem de pontos (l1, l2), isto é, o diagrama de dispersão.
- Considere as seguintes definições da janela de visualização:
Xmin = -1.2 ; Xmax = 8 ; Ymin = -0.5 e Ymax= 6.5.
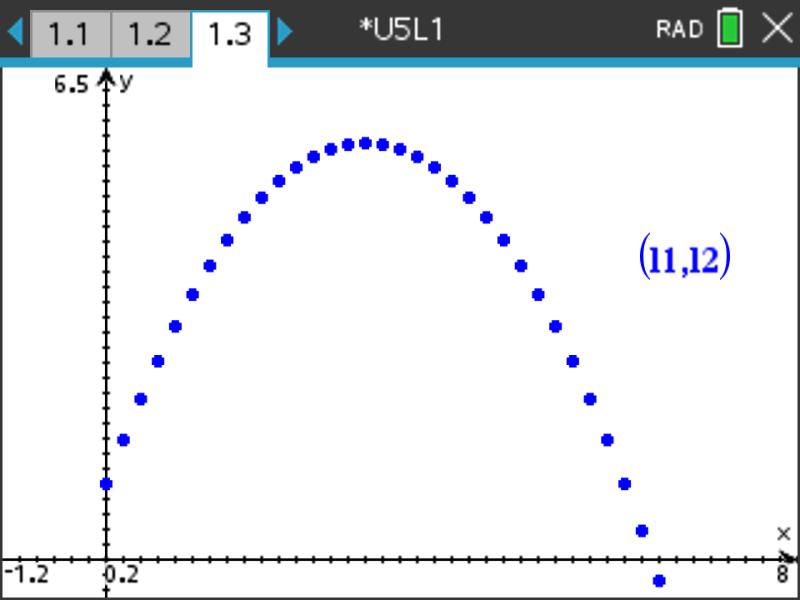
Passo 6
b) Importar dados de um programa em Python.
- Comece um novo script com o nome U5L1.
- A partir de
 importe a biblioteca TI System.
importe a biblioteca TI System. - Crie duas variáveis de listas (vazias) abcs e orda.
- Importe as bibliotecas TI System e TI PlotLib (não importa a ordem
) - Crie uma variável abcs e depois, a partir das opções da biblioteca TI System, escolha a opção 4: var=recall_list(" name"). Como as abcissas estão na lista l1, o campo "name" é preenchido com o nome da lista.
- Crie outra variável orda e proceda da mesma forma com a lista l2.
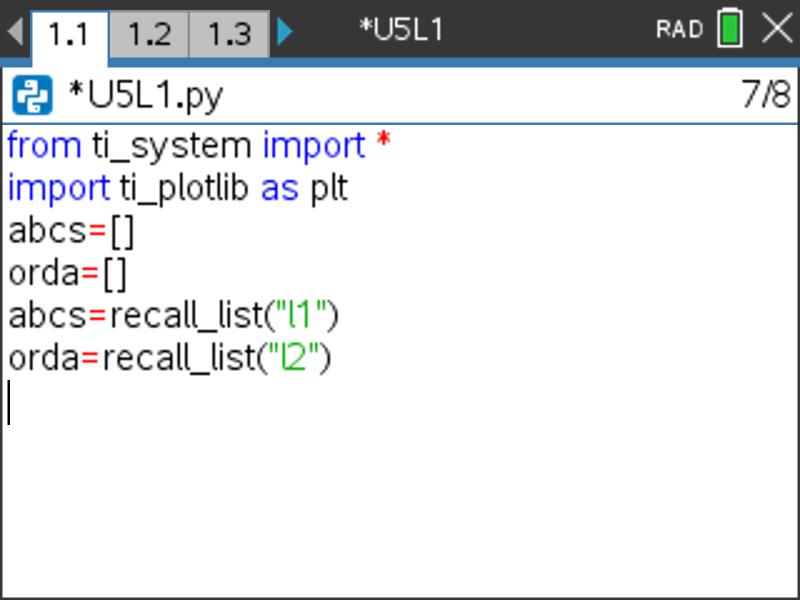
Passo 7
SUGESTÃO:
A criação de listas vazias abcs=[ ] e orda=[ ] não é obrigatória, pois elas serão criadas quando as listas l1 e l2 forem chamadas. No entanto, é bom manter os bons hábitos aprendidos quando não se utilizar o módulo TI System que requer essa criação prévia
- Execute o programa e depois verifique o conteúdo das variáveis abcs e orda pressionando a tecla
 .
. - Chame a lista abcs e valide-a

- Proceda da mesma forma com a lista das ordenadas (orda)
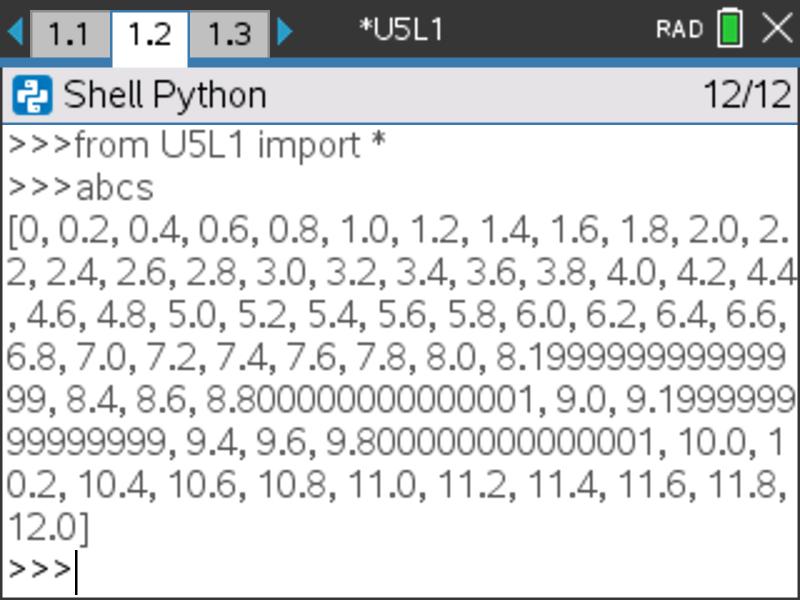
Passo 8
c) Representação gráfica.
Configure a representação conforme o ecrã ao lado.
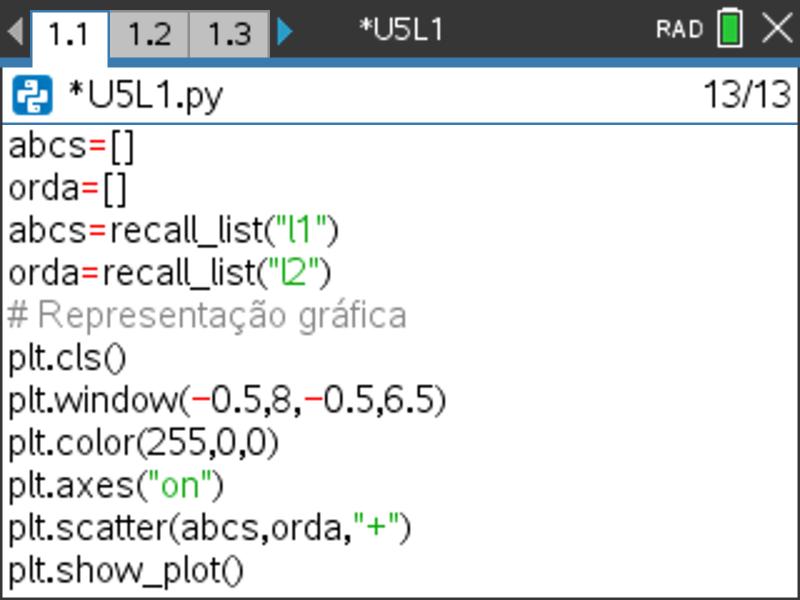
Passo 10
2: Exportar dados.
Crie um novo programa e designe-o por U5L11
SUGESTÃO:
Coloque o cursor no final duma linha e validar. Não importa a ordem da escrita da importação dos módulos.
- Crie uma função, nomeando-a por data (a,b,n).
- Crie duas listas de dados a serem representados na forma de nuvem de pontos com valores no intervalo [a; b], calculados com passo n.
- Na lista y, calcula-se a raiz quadrada dos valores da lista x.
- Para criar estas listas de dados podemos utilizar um ciclo FOR, naturalmente depois de criar duas listas vazias.
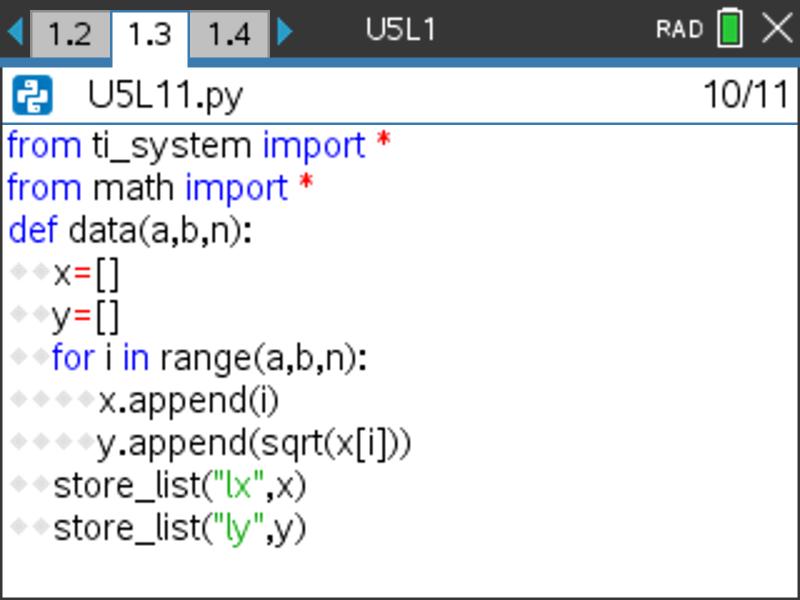
Passo 11
SUGESTÃO:
A criação de duas listas vazias permite evitar uma mensagem de erro durante a execução do programa.
NOTA:
Atenção à indentação, as instruções store_list não podem estar dentro do ciclo. Utilizar ![]() para suprimir níveis de deslocamento.
para suprimir níveis de deslocamento.
- Execute o programa. Tomamos aqui 20 valores, de 0 a 20 com passo 1
- Saia do ambiente Python e exiba a representação gráfica das listas lx e ly (nuvem de pontos na aplicação Gráficos, por exemplo).
Lição 2: Modelação
Descarregar documentos do professor / alunoNesta segunda lição da unidade 5, pode aprender como importar os resultados de um modelo utilizando a biblioteca TI System..
Objetivos:
- Efetuar modelação linear.
- Importar os resultados desta modelação num programa em Python.
Passo 1
Nesta lição trabalhará com um modelo linear a partir de dados inseridos previamente nas listas da calculadora. De seguida, vai escrever um programa para importar os dados desta modelação para os utilizar numa representação gráfica, numa interpolação, numa extrapolação …
Passo 2
O PROBLEMA
Num determinado dia, o pico de consumo de eletricidade é atingido por volta das 19 h. A nível nacional, é registado um pico de consumo de 96 350 megawatts às 19h02 do dia 15 de dezembro de 2019, uma quarta feira. Pretende fazer uma previsão dos picos de consumo no fim de semana seguinte para a zona abrangida pela central elétrica.
Para estabelecer essa previsão, tem dez leituras de consumo feitas às 19h, em função da temperatura, conforme apresentado na tabela abaixo
| T(oC) | 11 | -5 | -8 | -6 | 9 | 14 | 4 | -1 | -12 | 3 |
|---|---|---|---|---|---|---|---|---|---|---|
| MW | 3 | 5.7 | 6.6 | 6.3 | 3.4 | 2.7 | 4 | 5.1 | 7.1 | 4.6 |

Passo 3
- Os dados são inseridos em listas da calculadora, a temperatura em temp e o consumo em MW em cons.
- Para tal, abra uma aplicação de Listas e Folha de Cálculo, e de seguida introduza os dados.
NOTA
É também possível utilizar a aplicação Dados e Estatística, mas também a definição de listas numa aplicação Calculadora.
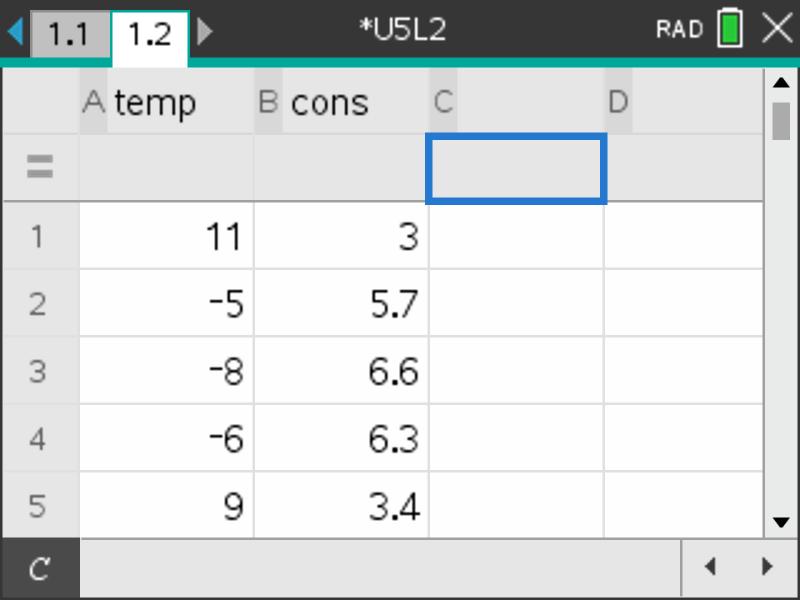
Passo 4
Efetuar uma regressão linear do tipo mx+b (![]() depois 4 Estatística).
depois 4 Estatística).
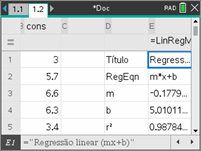
Passo 5
A fórmula permite prever o consumo em função da temperatura, que é
C = - 0.18 × t + 5.01 .
Representar numa aplicação Gráficos, a nuvem de pontos, bem como a reta de regressão.
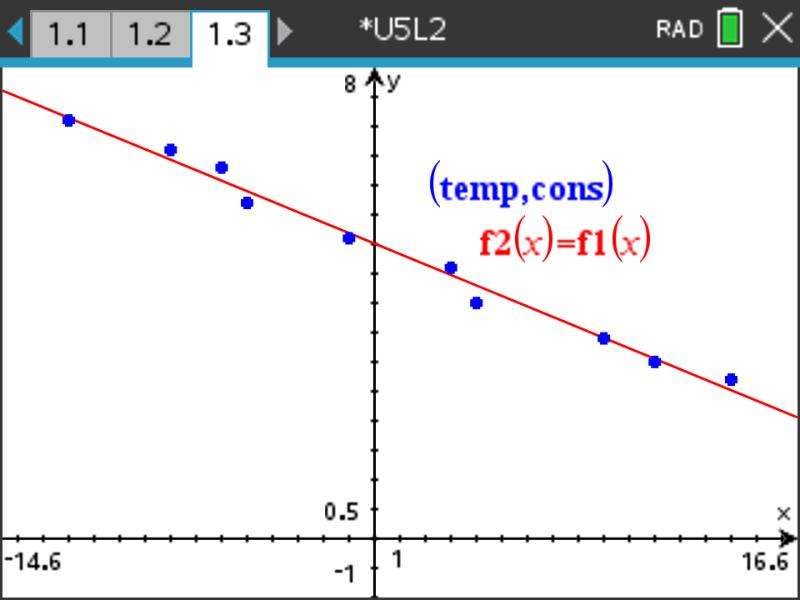
Passo 6
Utilização dos resultados da modelação num programa em Python.
- Começar um novo programa, nomeando-o como U5L2.
- Incorporar o menu TI System e TI PlotLib.
- Criar duas listas vazias, temperatura e consumo.
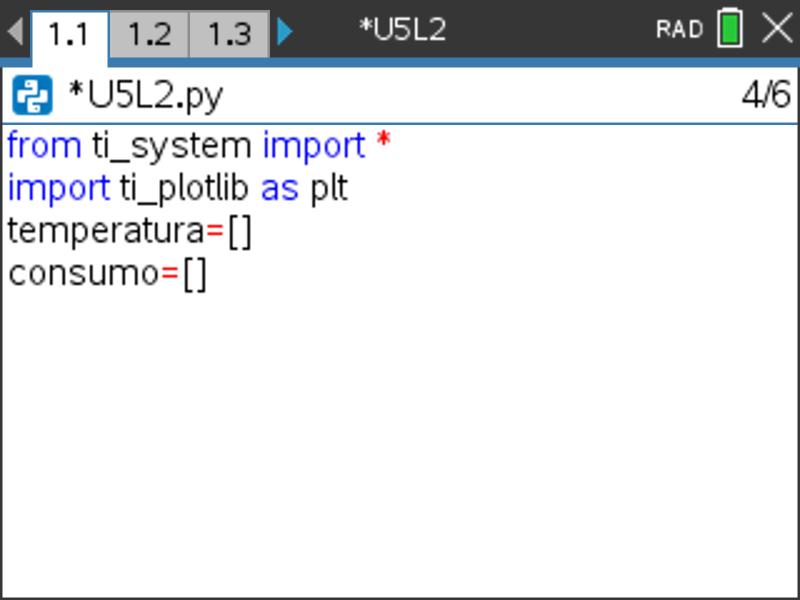
Passo 7
Atribuir o conteúdo das listas temp e cons nas respetivas listas novas.A instrução var=recall_list ( "name") está acessível no menu do módulo TI System(ver lição 1 da unidade 5).
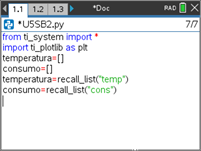
Passo 8
Testar o programa e solicitar a exibição das variáveis pressionando a tecla ![]() , escolhendo depois a variável pretendida.
, escolhendo depois a variável pretendida.
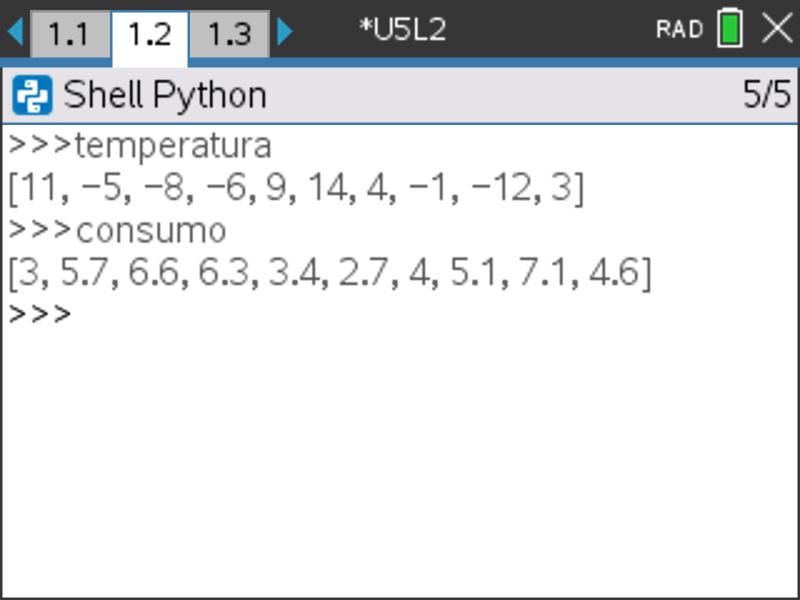
Passo 9
Para concluir esta lição e revisitar as lições da unidade 4, pode efetuar a representação gráfica das medições, bem como o modelo de regressão obtido.
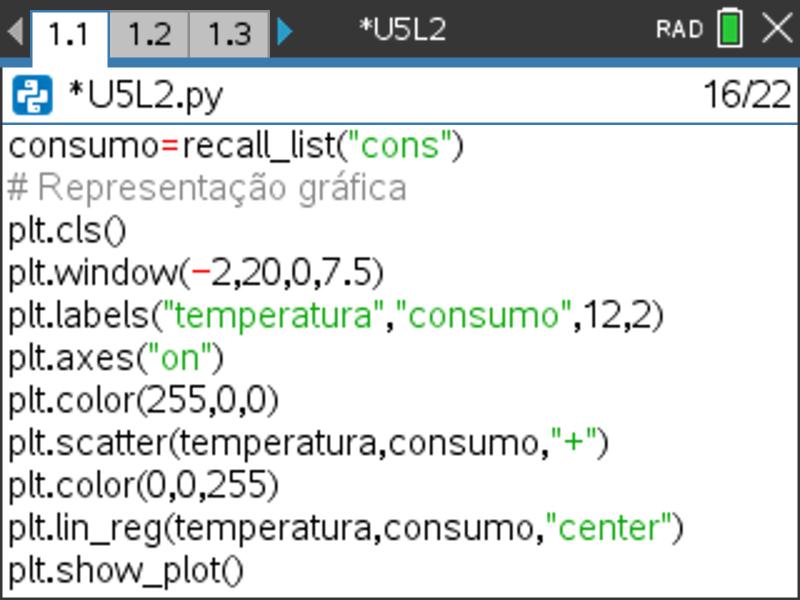
Passo 10
SUGESTÃO:
A instrução lin_reg(xliste, yliste, "marca", row) comporta um parâmetro suplementar row dando a possibilidade de colocar sobre outra linha a equação de regressão. Por defeito, é colocada na linha 11.
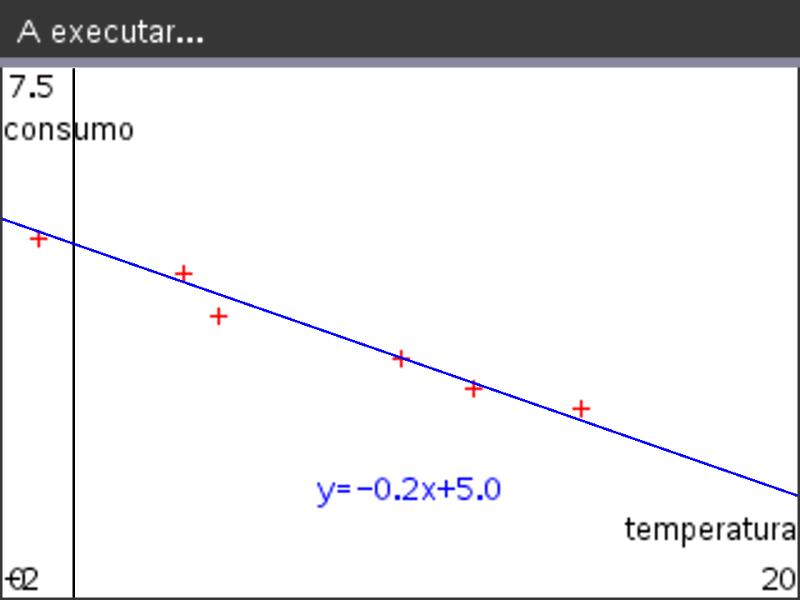
Passo 11
MAIS ALÉM:
Estimar o consumo de energia para uma determinada temperatura.Irá recuperar os coeficientes da reta m e b para os utilizar numa função que permitirá realizar uma estimativa do consumo de eletricidade quando se sabe a temperatura.
Definir uma função est(t) que dará o consumo estimado para uma temperatura t.
Executar o programa e efetuar alguns testes com diferentes temperaturas.
Lembre-se que o modelo apresentado representa uma estimativa de consumo às 19h02 em função da temperatura.
Pode então determinar os limites de validade do modelo.
- A instrução recall(value, "name") permite recuperar um programa, uma variável definida ou declarada numa aplicação.
- Atenção: as variáveis estatísticas têm um nome do tipo statn°.nome. Para as encontrar, pressione a tecla
 quando a aplicação estiver ativa.
quando a aplicação estiver ativa.
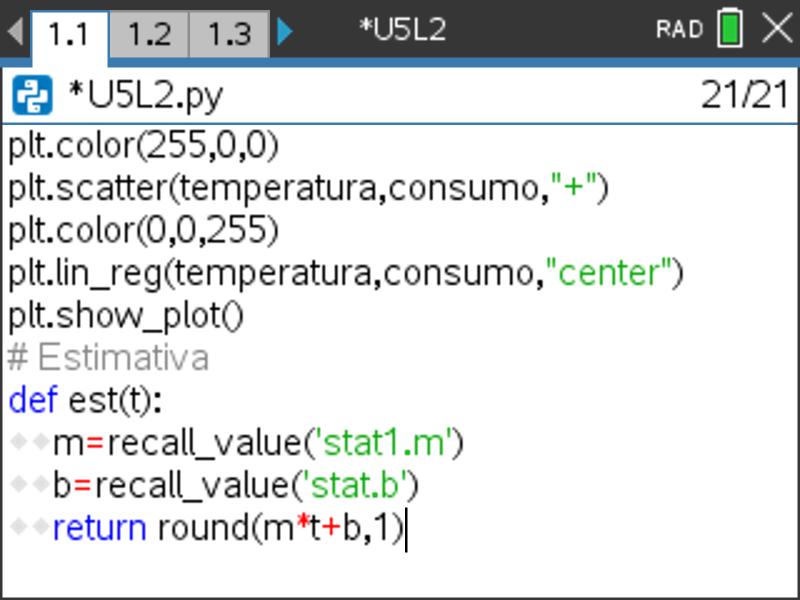
Lição 3: Exibição e temporização
Descarregar documentos do professor / alunoNesta terceira lição da unidade 5, poderá aprender como utilizar as opções de exibição e de temporização da biblioteca TI System do Python.
Objetivos:
- Compreender o funcionamento das instruções disp…
- Utilizar estas instruções num programa, para além dos outros módulos.
Passo 1
Nas primeiras duas lições desta unidade aprendeu como importar/exportar listas de dados e a trabalhar com uma equação de regressão.
A biblioteca TI System tem outras opções eventualmente úteis, que nos propomos descobrir aqui.
1: A instrução clear_history
- Iniciar um novo programa com o nome U5L3.
- Importar o módulo TI System.
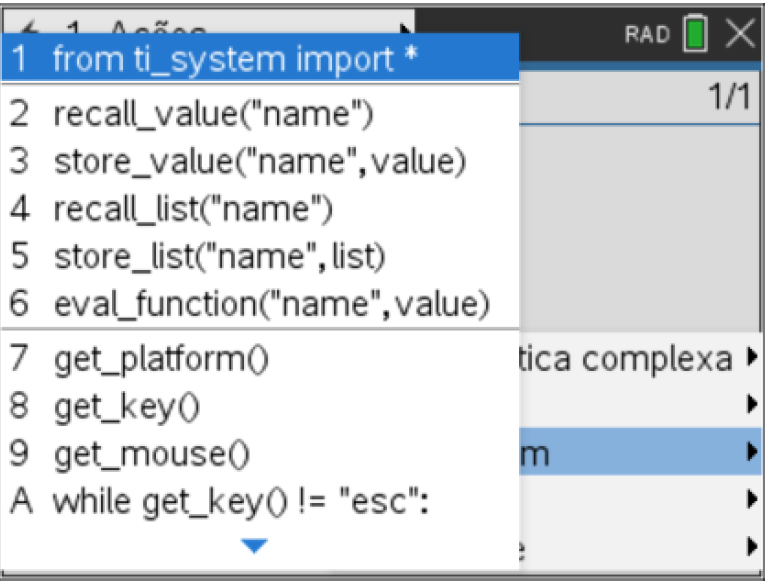
Passo 2
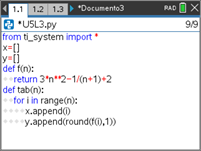
Passo 3
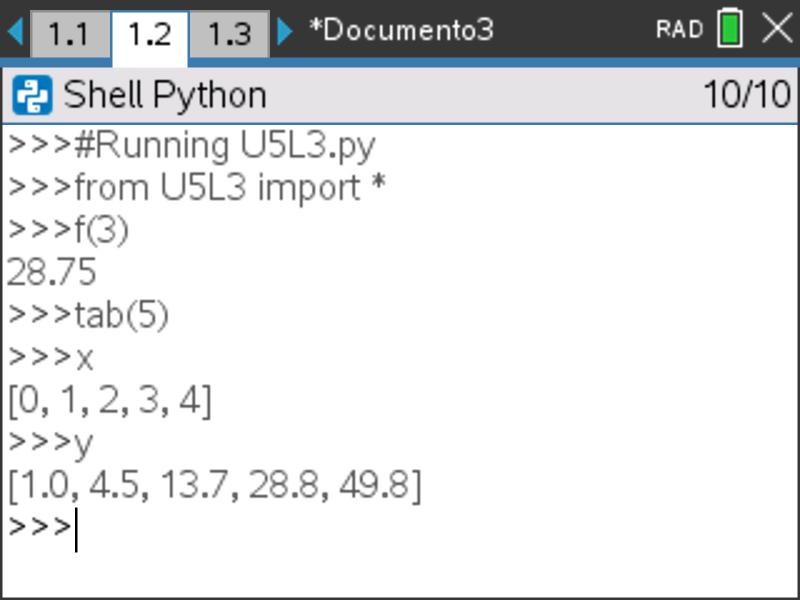
Passo 4
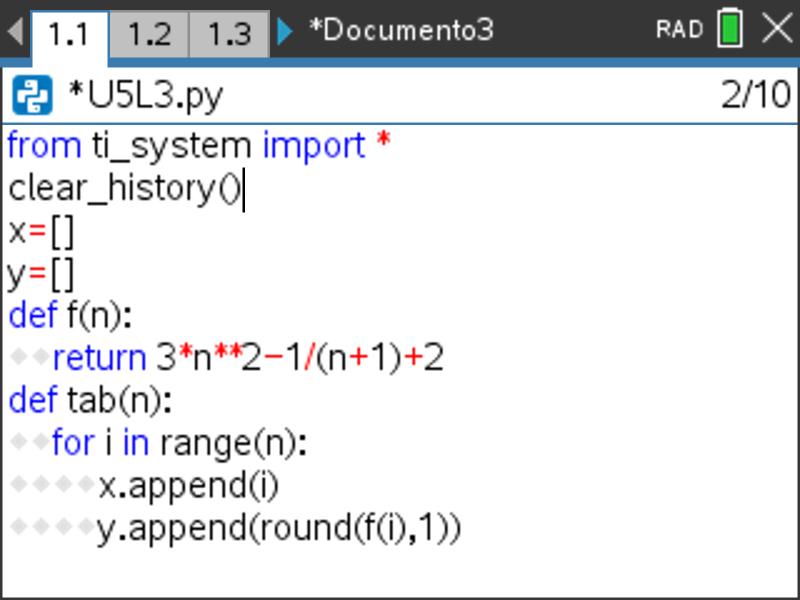
Passo 5
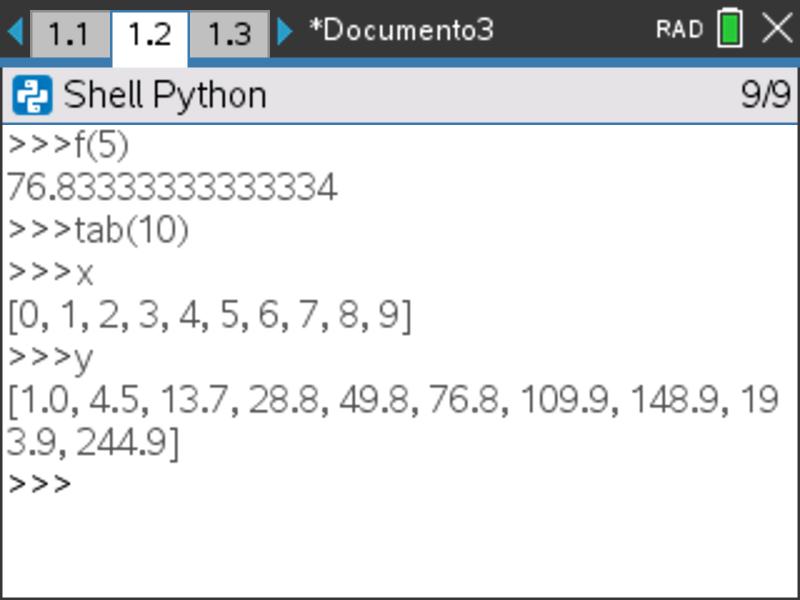
Passo 6
2: A instrução eval_function()
- Inserir uma página de Calculadora

 e definir a função:
e definir a função:
g: x→sin(x)
- A instrução eval_function() permitirá a utilização num programa em Python de uma instrução previamente definida noutra aplicação da TI-Nspire™ (Calculadora, Gráficos, Listas e Folha de Cálculo…).
Passo 7
Retome o programa e modifique-o como no ecrã para poder tabelar a função g: e depois representar graficamente a nuvem de pontos correspondente ao intervalo [0 ; 2π].
A instrução eval_function encontra-se no menu TI System, mas atenção à sintaxe.
eval_function("name",value): o argumento name será aqui g e não g(x)
Passo 9
- Executar o programa. Atenção, a unidade é, por defeito, o radiano.
- Veja as opções da biblioteca Maths para uma expressão da medida dos ângulos em graus ou uma conversão. (Unidade 1, Lição 1).
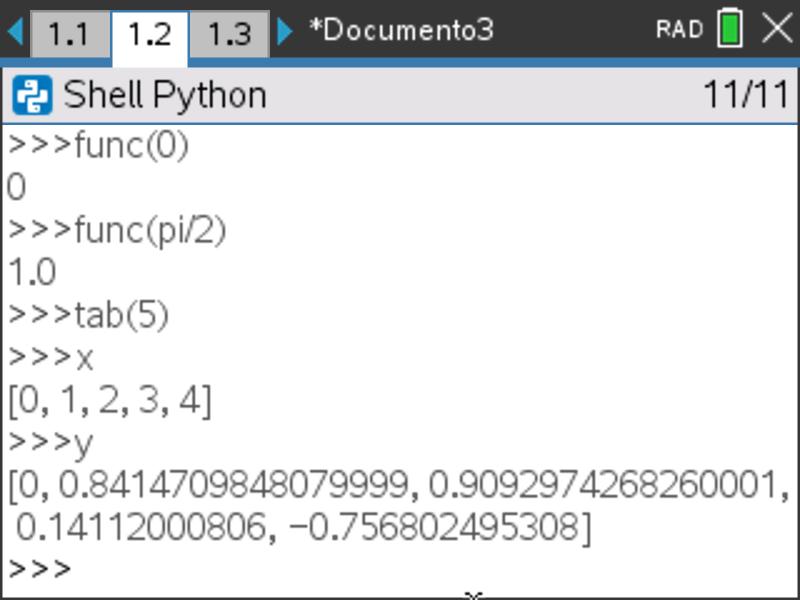
Passo 10
- Modificar novamente o programa para obter as coordenadas de n pontos de abcissa no intervalo [0 ; 2π]. Pode revisitar aqui o que aprendeu na unidade 4, lição 2.
- Terminar o programa, incluindo uma função graf( ).
- Verifique o funcionamento do programa.
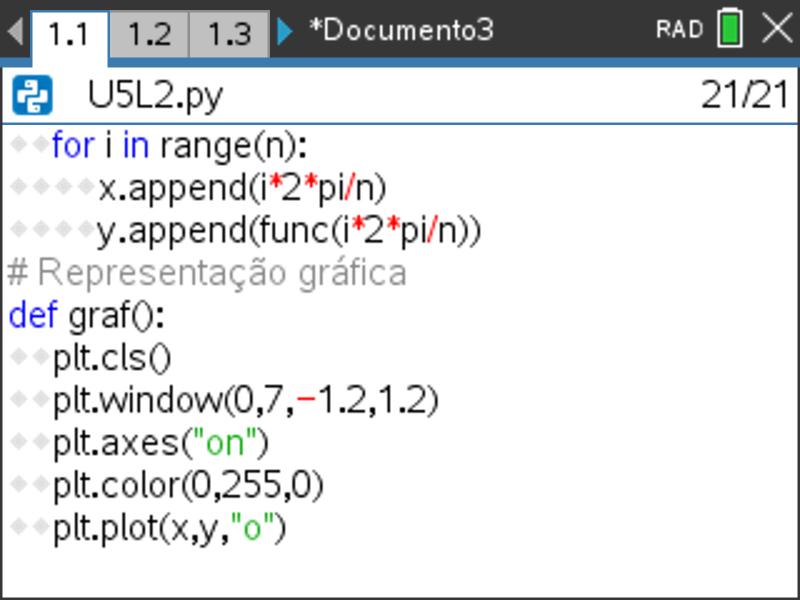
Aplicação: Estudo da queda livre
Descarregar documentos do professor / alunoNesta aplicação da unidade 5, pode revisitar as noções tratadas nas unidades 4 e 5 para criar um simulador que permita descrever um movimento.
Objetivos:
- Efetuar uma simulação de uma foto estroboscópica.
- Exportar os resultados para listas na calculadora.
Passo 1
Propõe-se, nesta aplicação relativa à unidade 5, utilizar a linguagem Python para criar um simulador de um fenómeno físico. Trataremos do estudo da queda livre:
- O programa deverá permitir a descrição de um movimento;
- A representação gráfica dos dados sob a forma de uma foto estroboscópica;
- Exportação dos dados para listas da calculadora.
O PROBLEMA:
Uma bola é lançada, sem velocidade inicial, de uma altura h.
As fotos são tiradas a cada 60 ms.
Vai escrever um programa que permita calcular, ao longo do tempo, a posição da bola, e depois fazer uma representação gráfica.
Passo 2
a) Cálculo das posições sucessivas
Durante a queda livre, a partir de uma posição inicial, e origem da marcação do tempo (y>0), a posição da bola pode ser calculada a partir da fórmula
y=-g/2×t2+h0
Note-se que: g≈9,81 m.s -2.
Criar um novo programa com o nome U5AP.
- Importar os módulos TI System e TI PlotLib.
- Limpar o ecrã.
- Criar uma função foto(h), com a altura inicial como parâmetro, que forneça a posição da bola em função do tempo.
- Criar três listas vazias, abcissa x, ordenada y e tempo te.
- A ordenada é calculada a cada 60 ms.
- Os valores são guardados nas listas se y >0 (a bola não passa do chão).
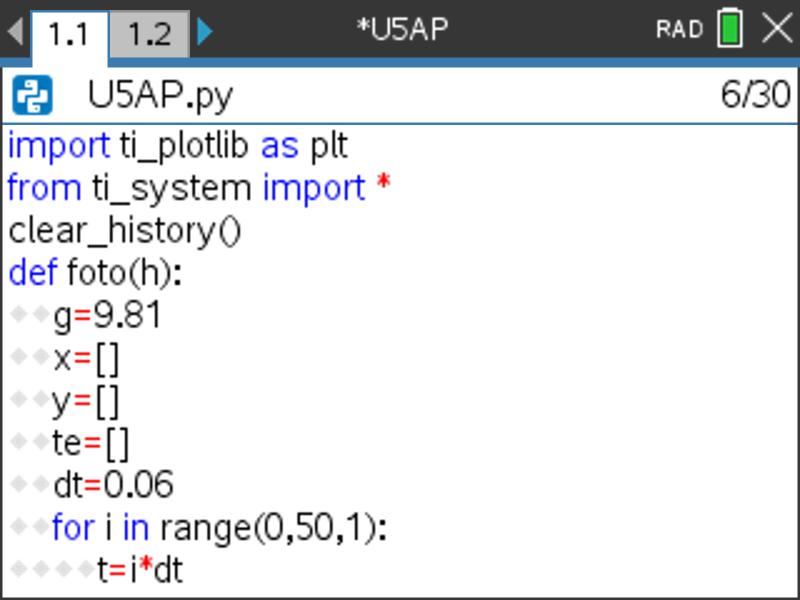
Passo 3
Criar um ciclo for para calcular a altitude da bola em função do tempo. Os resultados são expressos com precisão de 10-2 e armazenados nas respetivas listas. Como se pretende uma representação gráfica na forma de foto estroboscópica correspondente à realidade, a lista de abcissas será sempre 0. Finalmente, as listas te e y são exportadas respetivamente para as listas de tempo e de altura da calculadora.
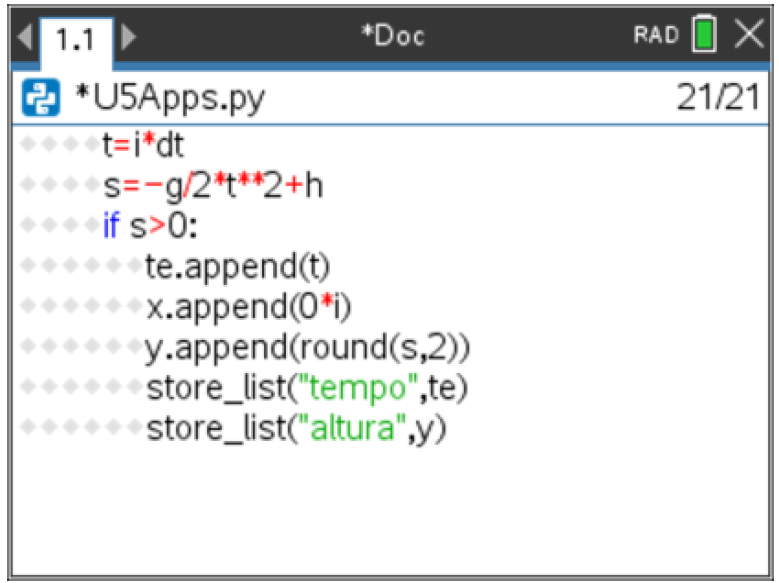
Passo 4
b) Representação gráfica
Configurar:
- Limpar o ecrã plt.cls( ).
- Exibir uma grelha de unidade 2 plt.grid(xscl, yscl, type,(r,v,b)).
- Definir uma janela para a representação plt.window(xmin, xmax, ymin, ymax).
- Definir a cor do ponto como magenta plt.color(255,0,255).
- Representar a nuvem de pontos plt.plot(x-list, y-list, mark).
- Exibir o gráfico plt.show_plot( ).
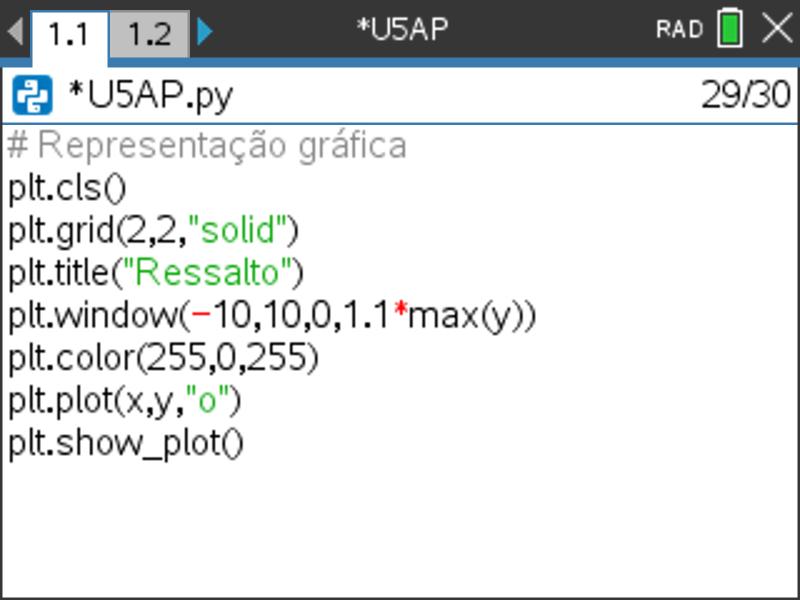
Passo 5
Executar o programa e pressionar a tecla ![]() , depois fornecer um valor para a altura inicial (8 m por exemplo).
, depois fornecer um valor para a altura inicial (8 m por exemplo).
Passo 7
SUGESTÃO:
A partir da lista de posições da bola, pode calcular-se a velocidade da bola e exibir os respetivos vetores.
Passo 8
c) Visualização dos dados exportados
- Sair do editor Python e exibir as listas.
- Inserir uma aplicação Calculadora.
- Obter as listas tempo e altura.
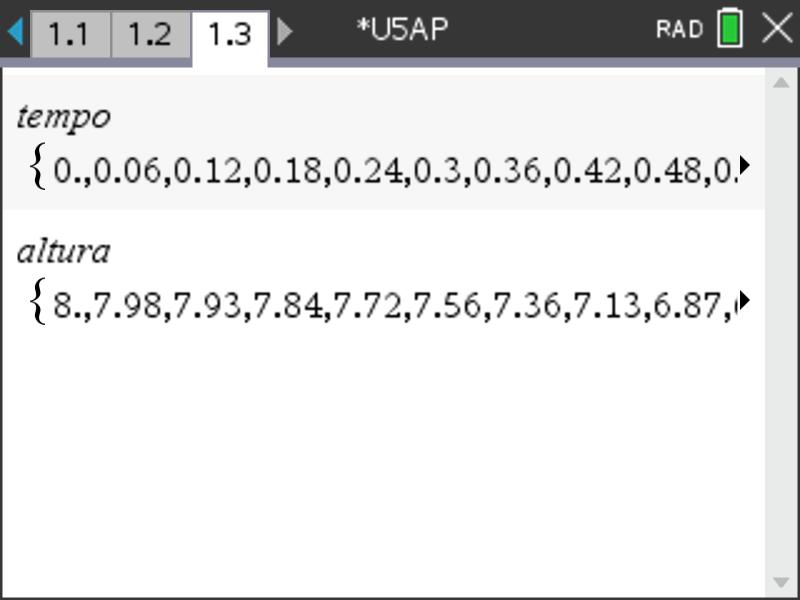
- Lição 1
- Lição 2
- Lição 3
- Aplicação
Unidade 6: Utilização das bibliotecas TI Hub & TI Rover
Lição 1: Os sensores integrados no Hub
Descarregar documentos do professor / alunoNesta primeira lição da Unidade 6 vamos aprender como utilizar a biblioteca TI Hub com o objetivo de controlar os dispositivos integrados no TI-Innovator™ Hub.
Objetivos:
- Explorar o módulo TI Hub.
- Escrever um programa integrando a biblioteca TI Hub para dispositivos integrados.
Passo 1
Nesta lição, iremos utilizar a biblioteca do TI Hub para observar visualmente uma mudança na luminosidade para, subsequentemente, simular uma mudança de crepúsculo ou para registar um conjunto de medições durante o nascer ou o anoitecer.
Começará, também, a considerar como associar esta biblioteca com aquelas que já conhece das Unidades anteriores (TI PlotLib e TI System) por forma a desenvolver um projeto científico completo.
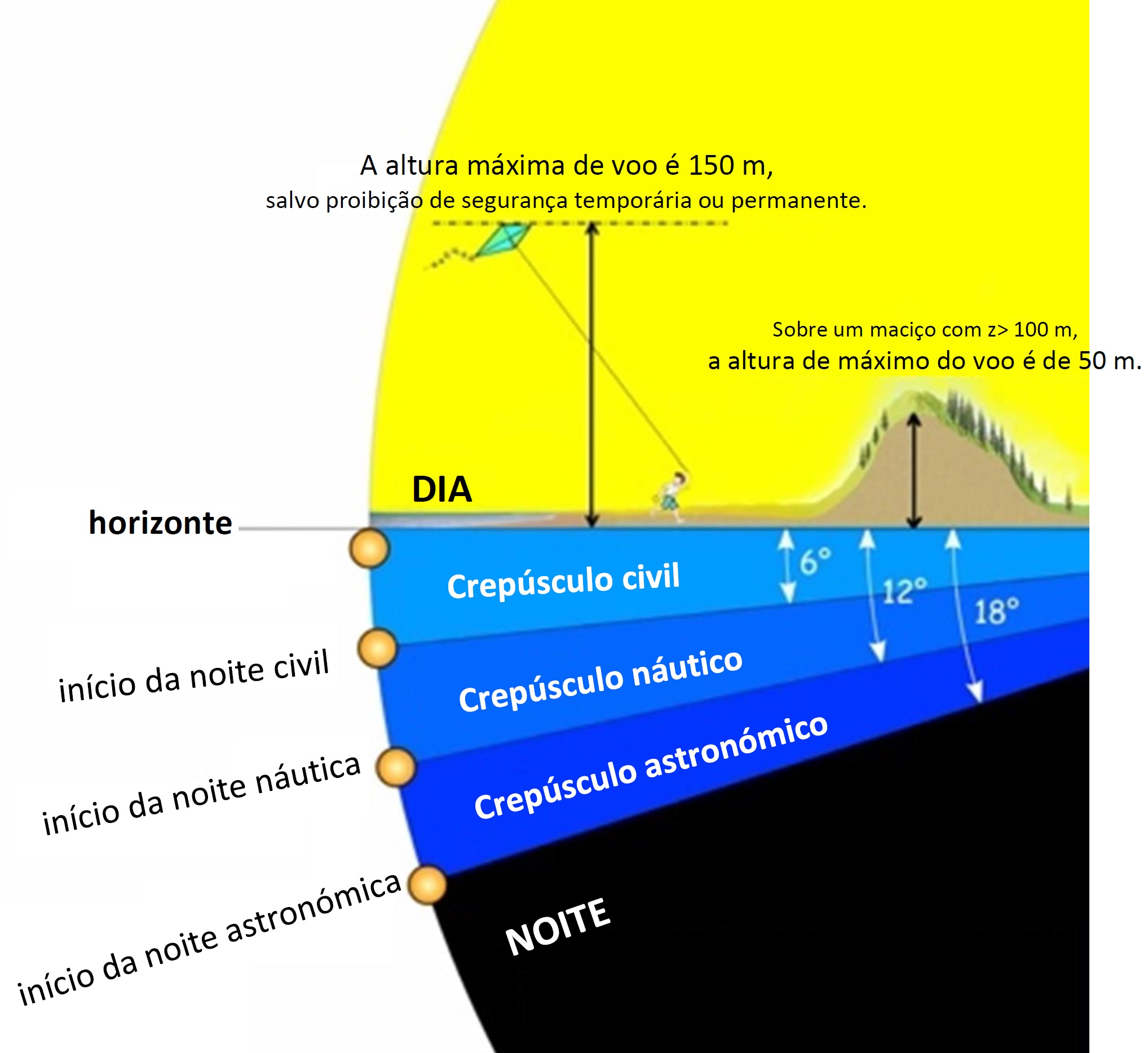
Passo 2
Considere o algoritmo simples que se apresenta abaixo, o programa que iremos elaborar basear-se-á nele.

Passo 3
IMPLEMENTAÇÃO DO PROGRAMA:
- Inicie um novo programa no editor de TI-Python, designe-o por U6L1
- Este programa deve integrar a biblioteca TI Hub, podendo optar por várias formas de o fazer:
- ao adicionar uma página com o editor de TI-Python, especificando o tipo geral de programa. Desta forma irá integrar, pelo menos, a biblioteca correspondente ao nome do tipo.
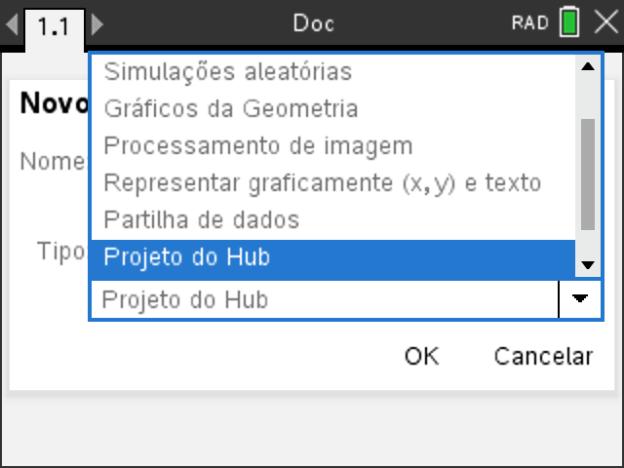
Passo 4
- Ou, também, pode começar com um programa em branco e, de seguida no início do programa, incorporar manualmente as bibliotecas de que necessita. Estratégia usada nas unidades anteriores.
Ao selecionar o tipo de documento como Projeto do Hub, irá obter um ecrã idêntico ao do lado. Ficarão ativas duas bibliotecas TI Hub e Matemática, e três funções de três bibliotecas diferentes. Por vezes é necessário adicionar mais bibliotecas, algo que se pode aperceber ao executar o programa.
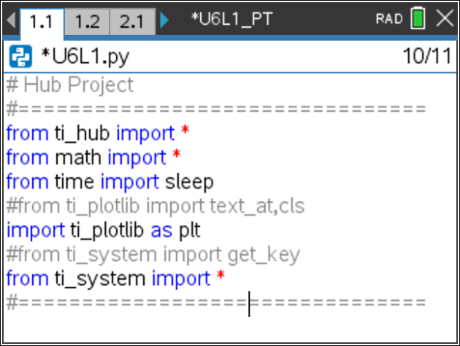
Passo 5
Usaremos o sensor de luz integrado no TI-Innovator, bem como o díodo RGB. Para que o programa seja capaz de os gerenciar, teremos de integrar as bibliotecas correspondentes. Para fazer isso, deve selecionar no menu o módulo 6: TI Hub, depois opção 1: Dispositivos integrados do Hub, e por fim 1: Saída de cor.
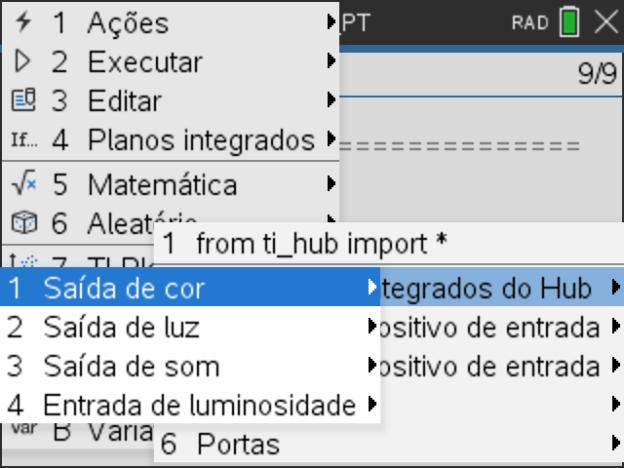
Passo 6
OBSERVAÇÃO:
As outras duas opções dizem respeito aos sensores e atuadores que serão conectados diretamente às portas de entrada IN ... e OUT ... do Hub ou possivelmente a outras portas.
- Para que o programa apresente as informações num ecrã "limpo", limpe-o usando a instrução clear_history() acessível através da biblioteca TI System. (Tecla
 , seguido de opção A: Mais módulos, depois 3: TI System e por fim B: clear_history())
, seguido de opção A: Mais módulos, depois 3: TI System e por fim B: clear_history())
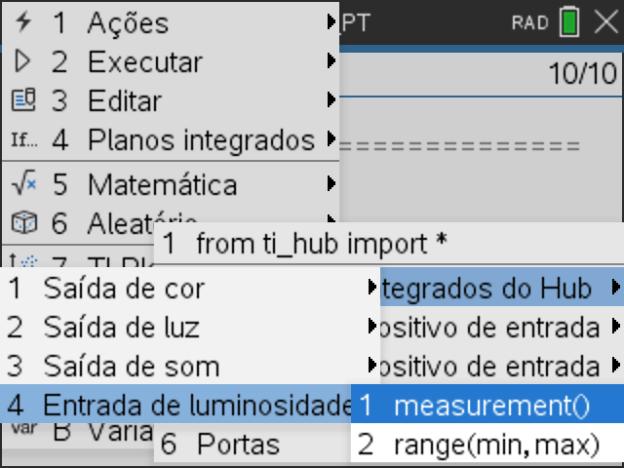
Passo 7
- Crie uma variável lum0, à qual deve atribuir a medida de luminosidade do momento. A instrução brightness.measurement() está no módulo 8: TI Hub , depois opção 2: Dispositivos integrados do Hub , seguido de 4: Entrada de luminosidade, e por 1: measurement().

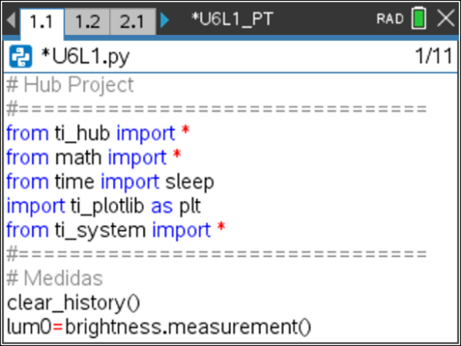
Passo 8
- De seguida insira o código que permita o programa exibir uma mensagem solicitando que o utilizador altere a intensidade da luz nas proximidades do sensor integrado: plt.text_at(). Esta função e a função cls(), para limpar a janela gráfica, encontram-se no módulo 7: TI PlotLib.
- Adicione um tempo de espera, função sleep(), que será útil para efetuar alteração da intensidade da luz. (Tecla
 , seguido de opçãoA:Mais módulos, depois 2:Time e por fim 2: sleep(seconds))
, seguido de opçãoA:Mais módulos, depois 2:Time e por fim 2: sleep(seconds)) - Crie uma nova variável lum1 à qual irá atribuir o valor da nova medição da intensidade luminosa.
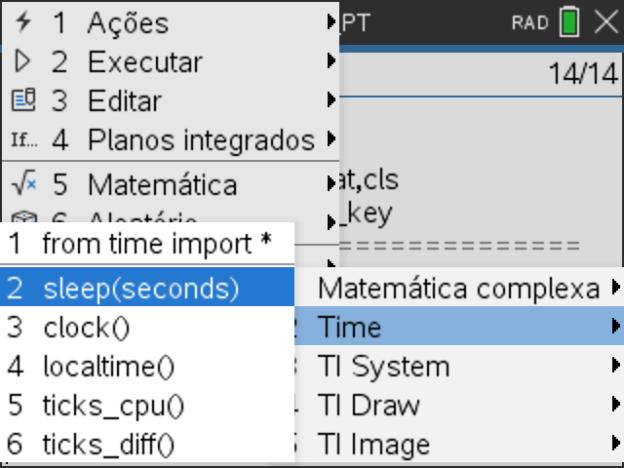
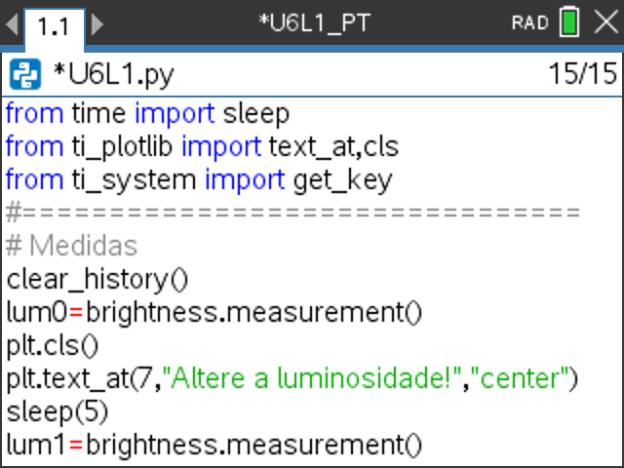
Passo 9
- Por fim a comparação entre as medidas lum0 e lum1. Utilizando a estrutura de controlo condicional IF e em função do resultado lógico da condição lum0 > lum1, o LED RGB ficará verde ou vermelho durante 2 segundos. Caso lum0 = lum1, não ocorrerá nada!
- As funções color.rgb(Red,Green,Blue) e color.off() encontram-se no módulo 8: TI Hub, depois opção 2: Dispositivos integrados do Hub, seguido de 1: Saída de cor
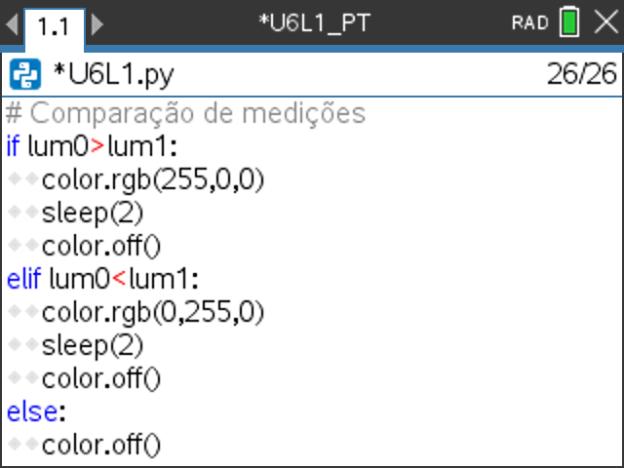
Passo 10
SUGESTÃO:
Pode acrescentar ao seu programa uma instrução que lhe permita observar, no ecrã da unidade portátil, qual a cor que deverá surgir no Hub em função das medidas, para isso bastará acrescentar uma instrução de texto após cada teste. Esta estratégia poderá ser útil para validar programas e verificar se o resultado é o esperado.
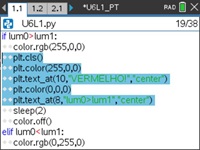
Passo 11
EXTENSÃO DA ATIVIDADE:
Faça uma cópia do programa anterior, designe-o por U6L1ext e mova-o para um Problema 2 do seu documento tns. Para mover uma página entre Problemas pode usar a vista de Gestor de Página, clicando ![]() e usar o menu de contexto,
e usar o menu de contexto, ![]() , sobre a página a mover.
, sobre a página a mover.
Também poderá, se entender, abri um novo documento e começar de início o programa.
Altere o programa de forma que registe as medidas de luminosidade ao longo de 40 minutos.
Passo 12
OBSERVAÇÃO:
Note que o sensor de intensidade luminosa do TI-Innovator não é calibrado em Lux, mas isso não é problema, pois estamos interessados apenas nas variações de intensidade e não em sua medida em Lux.
No programa, as medidas da intensidade luminosa serão guardadas numa lista, que designaremos por r, que a iniciaremos como vazia r=[ ]. O registo dos tempos de recolha dos dados serão também guardados numa lista,t[ ].
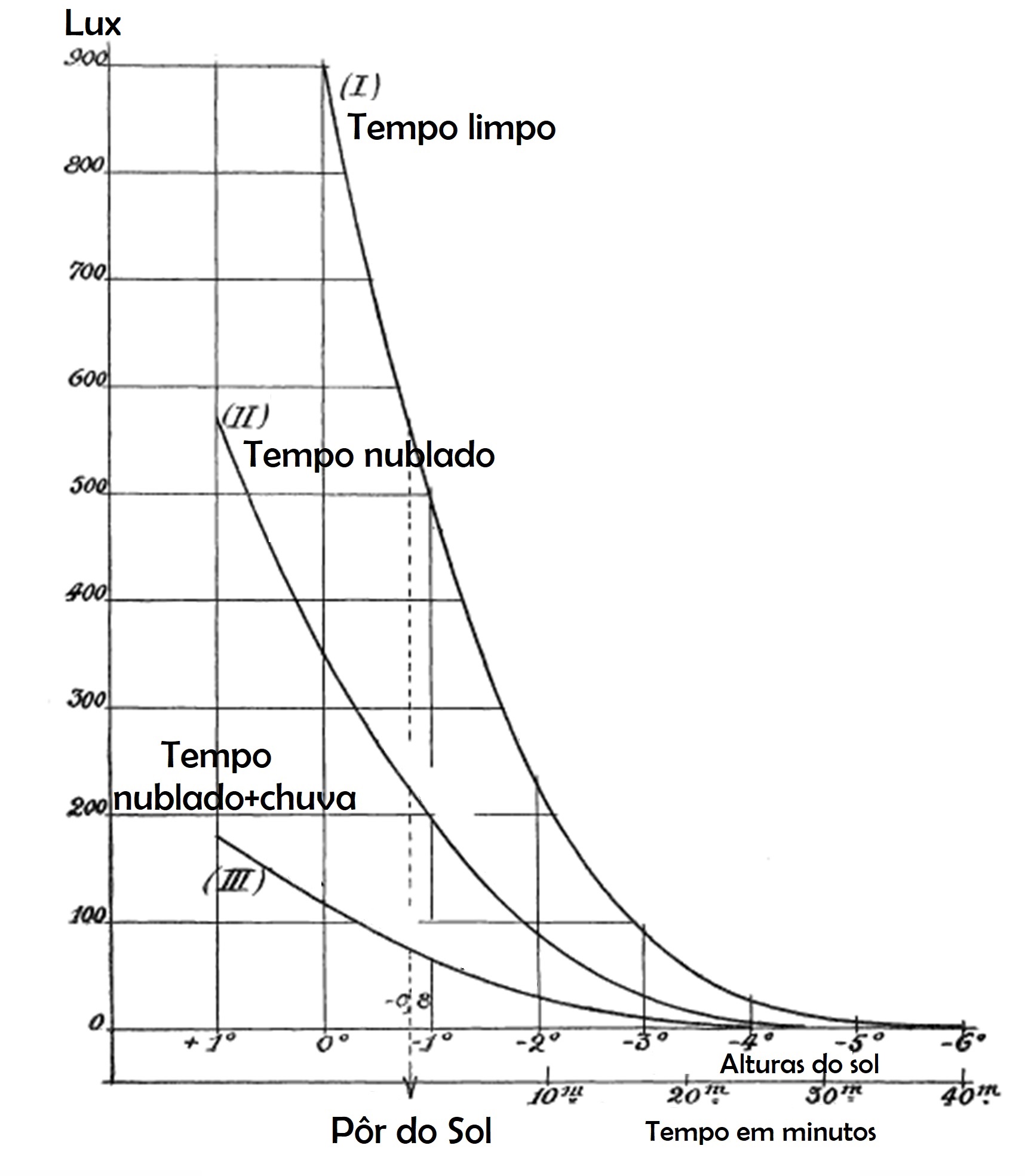
Passo 13
Abaixo, no ecrã da esquerda, propõe-se o código para a parte do programa que executará a recolha de dados e os guardará em listas, (#Recolha de dados), e à direita encontra-se um ecrã com o código relativo à representação gráfica dos dados, (#Representação gráfica).
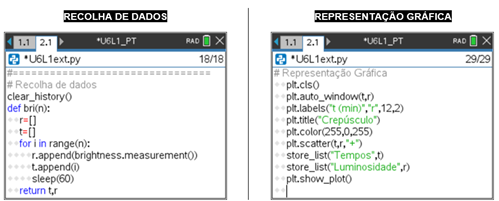
Passo 14
OBSERVAÇÃO:
No ecrã da direita, também se apresenta a proposta de exportação dos dados para listas das restantes aplicações da TI-Nspire CX II, podendo ser exploradas, por exemplo, na aplicação Listas e Folha de Cálculo.
- A função store.list() encontra-se no menu A: Mais módulos, na opção 3: System e depois opção 5: store.list(“ name”,list ).
- A função ,bri(n) realiza aquisição de dados a cada minuto, dada a instrução sleep(60), por n minutos e retorna as listas t e r.
- De seguida são representados graficamente os dados constantes nas listas t te r e exportados para as listas Tempos e Luminosidade da TI-Nspire CX II
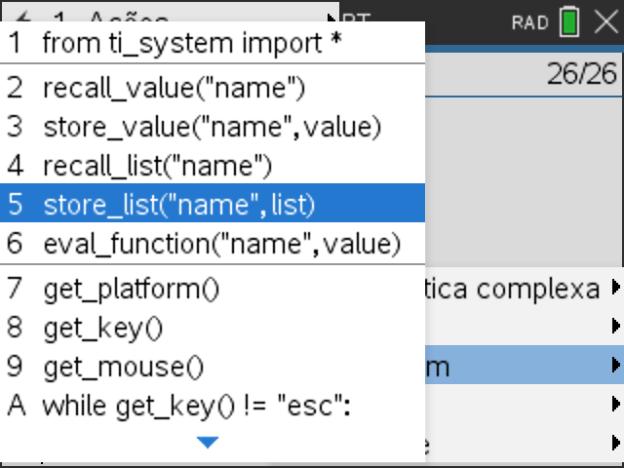
Lição 2: Dispositivos de entrada e saída
Descarregar documentos do professor / alunoNesta segunda lição da Unidade 6 vamos aprender como conectar e utilizar um dispositivo, de entrada e saída, integrado no TI-Innovator™ usando a biblioteca TI Hub.
Objetivos :
- Explorar o módulo TI Hub.
- Escrever e utilizar um programa para usar um componente de entrada/saída
Passo 1
Nesta lição, iremos utilizar um componente essencial em qualquer cadeia de medição usando sensores: o potenciómetro.
Um potenciómetro é um tipo de resistor variável com três terminais, um dos quais está conectado a um cursor que se move numa trilha resistiva terminada pelos outros dois aos quais a resistência está sujeita.
Os potenciómetros são comumente usados em circuitos eletrónicos. Eles são usados, por exemplo, para controlar o volume de um rádio. Os potenciómetros também podem ser usados como transdutores, pois convertem uma posição em uma tensão. Esse tipo de dispositivo pode ser encontrado em joysticks.
Vamos agora escrever um programa para medir a tensão elétrica entre dois terminais do potenciómetro e, em seguida, apresentar no ecrã.
OBSERVAÇÃO:
O objetivo desta lição não é estudar o componente em si, mas sim integrá-lo num programa Python para se obter os dados que ele fornece. Portanto, o programa que irá ser criado será facilmente transponível para qualquer outro tipo de transdutor.

Passo 2
IMPLEMENTAÇÃO:
- Inicie um novo programa no editor de TI-Python, designe-o por U6L2.
- Selecione tipo de programa Projeto do Hub, desta forma automaticamente as bibliotecas TI Math e TI Hub serão importadas.
- Agora, necessitará de ainda de importar as bibliotecas TI System e Time, acessíveis na opçãoA: Mais módulos do menu, e eventualmente necessitará também da biblioteca TI Plot.
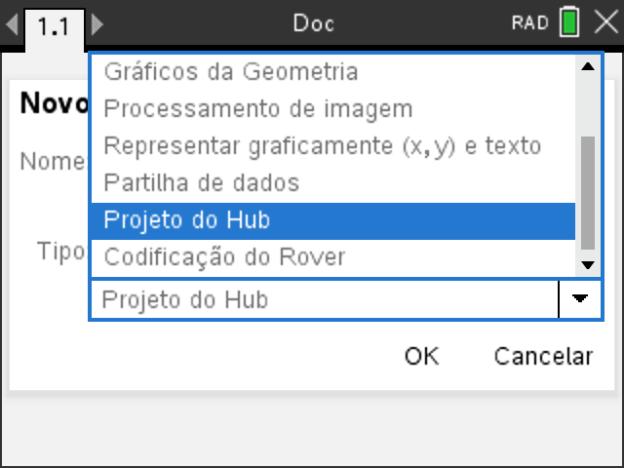
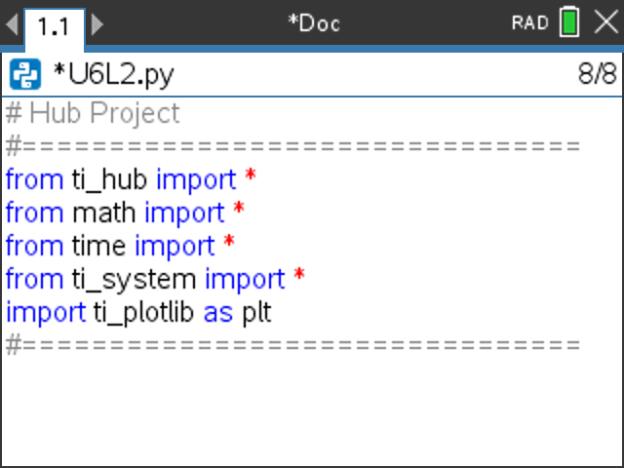
Passo 3
- Crie uma função pot() sem qualquer argumento.
- Apague o ecrã usando a instrução clear_history() localizada na biblioteca TI System.
- Na biblioteca TI Hub, selecione o menu 3: Adicionar uma unidade de entrada e de seguida A: Potenciómetro.
- Atribua o valor a ser registado pela função potentiometer ("porta") à variável mes.
- Conclua esta instrução definindo como argumento da função potentiometer("porta") a porta In1(entrada 1).
- Utilizando a tecla
 pode preencher os campos da função de forma automática e mais rápida.
pode preencher os campos da função de forma automática e mais rápida.
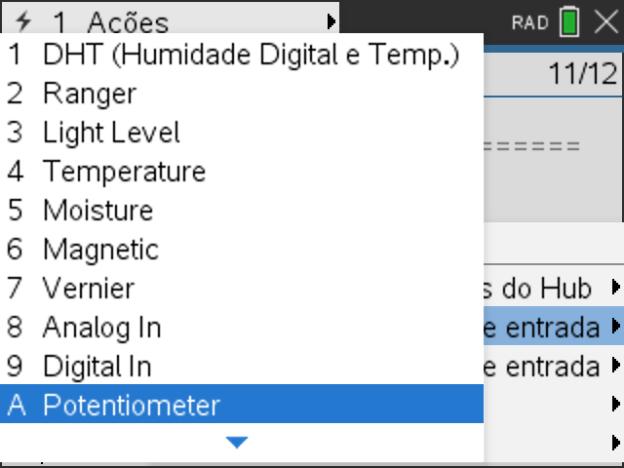
Passo 4
OBSERVAÇÃO:
Todos os sensores (dispositivos de entrada) têm um mínimo de duas variáveis:
1: var=sensor("porta") e 2: var.measurement() .
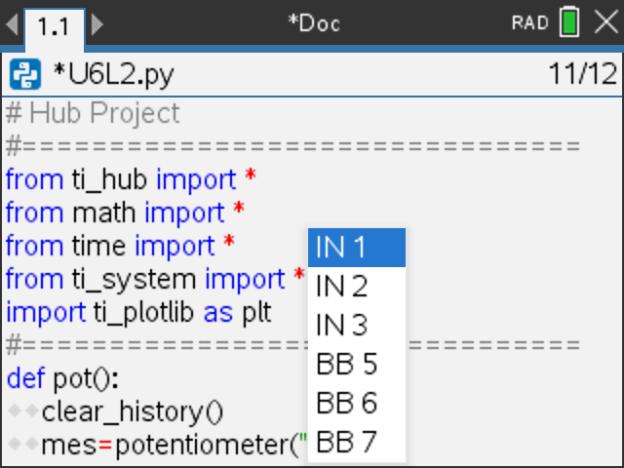
Passo 5
- Crie uma variável v que permita recolher a medição do sensor conectado (variável mes ). No editor de programas, surgirá a proposta de preenchimento automático assim que se escreva v=mês., abrindo uma janela com as opções. A opção measurement() não está disponível no menu TI Hub.
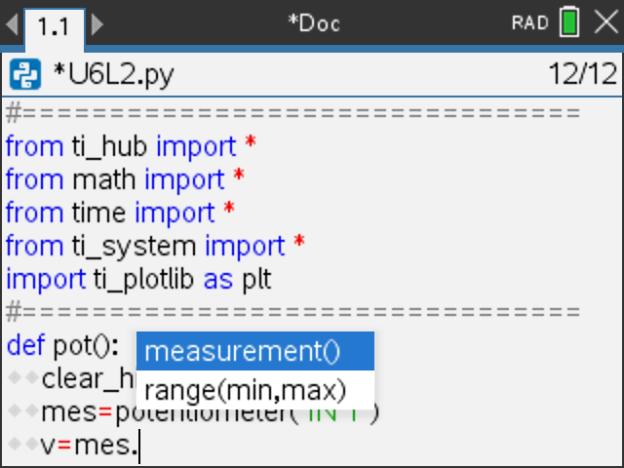
Passo 6
- Verifique o funcionamento do seu sensor após ter colocado previamente o potenciómetro na posição central.
- Conecte o TI-Innovator™ à calculadora e, em seguida, o potenciómetro à porta IN1 do Hub.
- Execute o programa, e no interpretador execute a função pot().
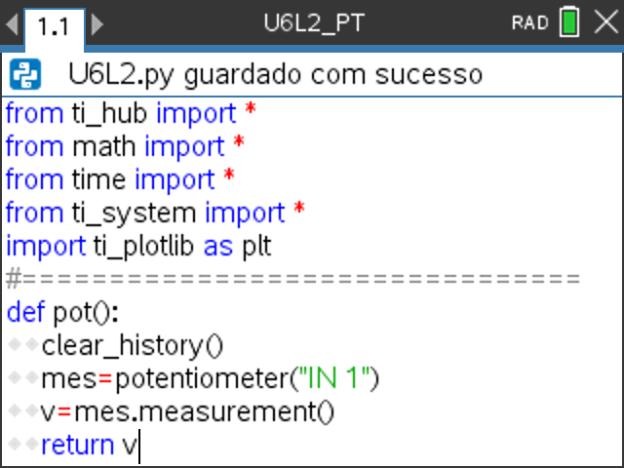
Passo 7
Deverá obter dados da mesma ordem de magnitude do ecrã ao lado, mas observe que não é uma tensão, pois seu potenciómetro é alimentado por uma tensão de 3,3V. O valor a ser encontrado pertencerá ao intervalo [0; 3,3].
- Efetue uma cópia do programa através do menu, tecla
 , e da opção 1:Ações, seguido da opção 3:Criar uma cópia. Designe a cópia do programa por U6L22.
, e da opção 1:Ações, seguido da opção 3:Criar uma cópia. Designe a cópia do programa por U6L22.
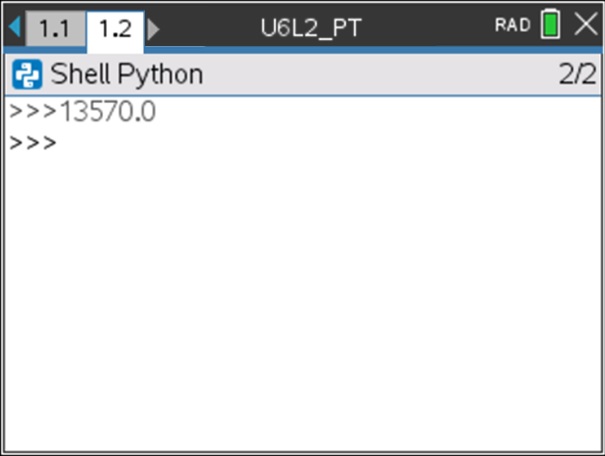
Passo 8
- Altere o programa para levar em consideração a resolução do conversor analógico para digital (14 bits). Assim, a medição da tensão será:
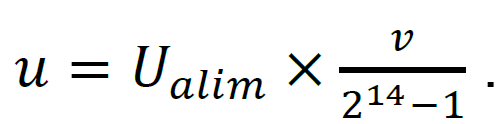
- O valor final da tensão será arredondado às centésimas.
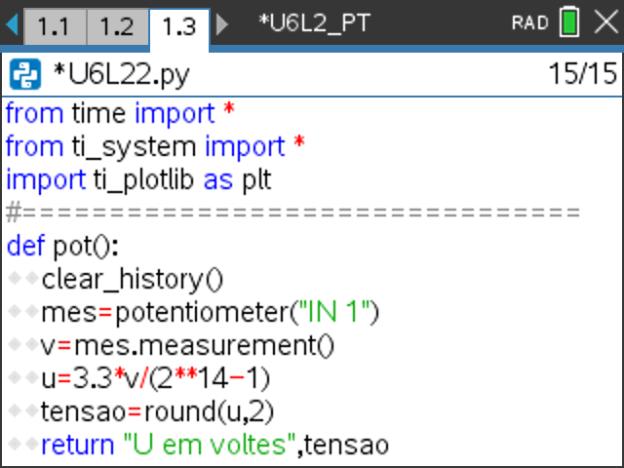
Passo 9
- Execute o programa U6L22, atalho
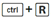 , e no interpretador execute a função pot().
, e no interpretador execute a função pot().
Passo 10
MAIS ALÉM:
Algumas ideias para possíveis extensões da lição:
- Use um potenciómetro para construir um sensor angular (uma medição de tensão corresponde ao valor de um ângulo lido em um transferidor), a seguir faça a representação gráfica da função modelada α = f (u).
- Entre 0 e 3,3 V, associe uma faixa de tensão com uma cor usando o LED RGB TI-Innovator™.
- Associe a medição da tensão com as coordenadas de um ponto marcado (princípio de um joystick).
- Etc ...
Lição 3: Dispositivos de entrada e saída
Descarregar documentos do professor / alunoNesta terceira lição da Unidade 6 vamos aprender como conectar o TI-Rover usando a biblioteca TI Rover.
Objetivos:
- Explorar o módulo TI Rover.
- Escrever e utilizar um programa para usar o TI-InnovatorTM Rover e os periféricos associados.
- Usar um ciclo aberto e uma função condicional.
Passo 1
Nesta lição, iremos criar um programa que permita ao TI-Innovator™ Rover ter a possibilidade de realizar um trajeto marcado pela iluminação do díodo RGB, desde que a distância (medida pelo sensor RANGER) respeite um limite definido numa função condicional.


Passo 2
IMPLEMENTAÇÃO DO PROGRAMA:
- Inicie um novo programa no editor de TI-Python, designe-o por U6L3.
- Selecione tipo de programa Codificação do Rover, desta forma automaticamente as bibliotecas TI Math, TI System e Time, serão importadas. Também o módulo TI PlotLib ficará implementado.
- Agora, poderá começar a escrever o programa.
Passo 3
- Apague o ecrã usando a instrução clear_history() localizada na biblioteca TI System.
- Para o utilizador interromper o movimento do Rover vamos usar como estratégia colocar o núcleo do programa dentro de um ciclo de controlo While, interrompido quando o utilizador clicar na tecla
 . Comecemos por apresentar essa informação ao utilizador usando a função plt.text_at(linha, “texto”, alinhamento) do módulo TI PlotLib.
. Comecemos por apresentar essa informação ao utilizador usando a função plt.text_at(linha, “texto”, alinhamento) do módulo TI PlotLib.
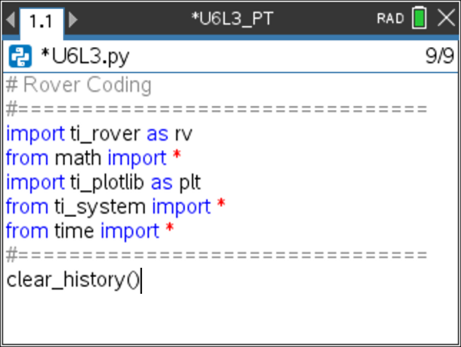
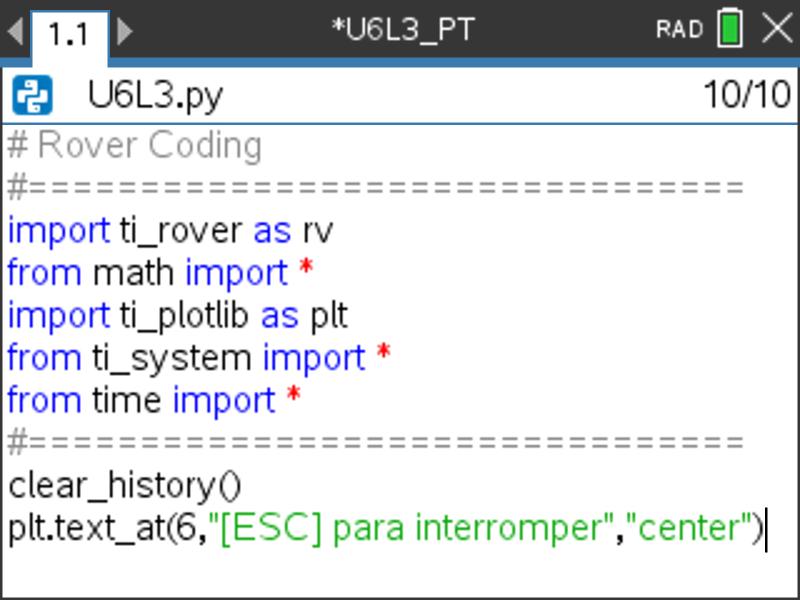
Passo 4
- Dê instruções ao TI-Innovator™ Rover para avançar. A unidade de medida da distância será uma sua opção, sabendo que, por defeito, está definida como 0,1 m. Assim, rv.forward (20) fornecerá ao Rover informação para ele se mover para frente uma distância de 2 m. A instrução rv.forward() está localizada no menu 9: TI Rover e, de seguida, em 2: Condução, e por fim 1: forward(distance).
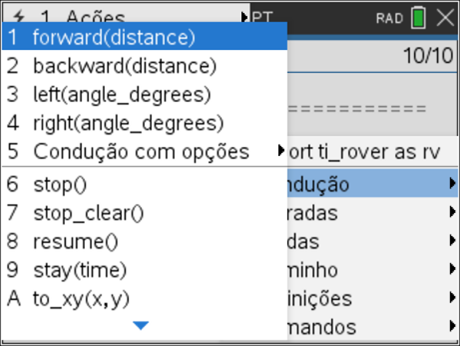
Passo 5
- Em seguida, insira o início de um ciclo While já predefindo para a nossa estrategia de interrupção do programa, que pode ser obtido no menu da biblioteca TI System (opção A: Mais módulos do menu).
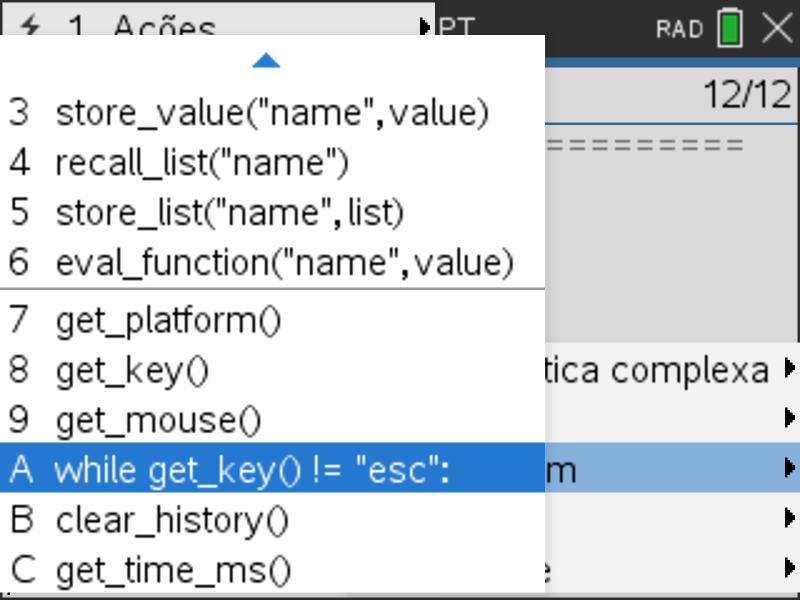
Passo 6
NOTA:
Algumas das instruções disponíveis na biblioteca TI System, também estão disponíveis na bibloteca TI Rover na opção 7: Comandos.
- Crie uma variável a à qual será atribuida a distância medida pelo RANGER. Para isso, comece por escrever a letra a=, depois insira a instrução rv.ranger_measurement() localizada no menu 9: TI Rover e 3: Entradas, e finalmente 1 rv.ranger_measurement(). A unidade de medida é o metro.
Passo 7
- Agora, implemente a estrutura condicional do nosso algoritmo. Se a distância medida for inferior a 20 cm, o ROVER irá parar e o LED RGB acenderá em vermelho. A instrução rv.color_rgb() está disponível na biblioteca 9:TI Rover, na sua opção 4: Saídas, e por fim 1: color_rgb(r,g,b).
Passo 8
- A instrução rv.resume() termina o processamento de ações na fila, e desta forma não teremos sobreposições de instruções sobre o ROVER. Esta função está localizada no menu 9: TI Rover e, de seguida, em 2: Condução, e por fim 8: resume().
Passo 9
- Iremos utilizar a função rv.stop() para parar o ROVER, sendo uma instrução de condução está, portanto, localizada no menu correspondente do módulo TI Rover. Caso contrário, o díodo RGB fica verde e o ROVER continua o seu percurso até encontrar a distância definida.
Passo 10
- Por fim, após o ciclo, inserir as seguintes instruções:
- Parar o ROVER - rv.stop() ;
- Apagar o ecrã - clear_history() ;
- Exibir a cor azul no díodo - rv.color_rgb(0,0,255) .
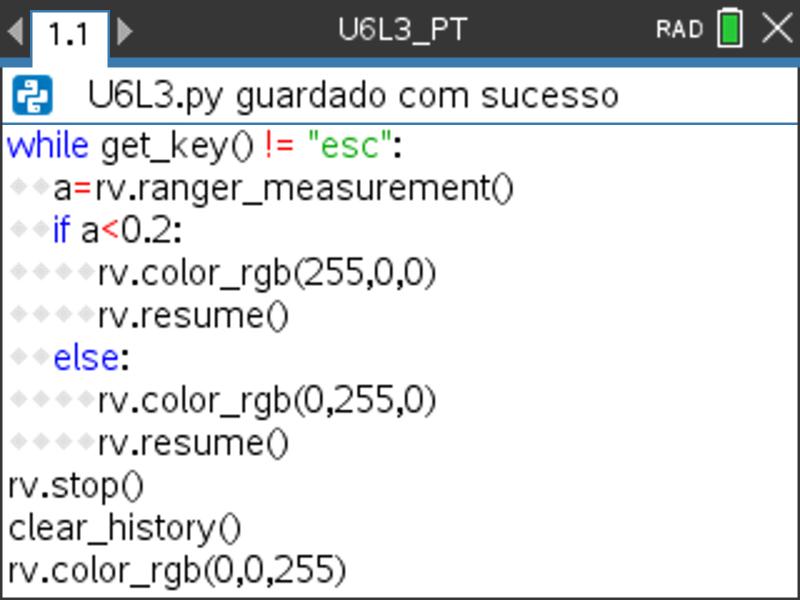
Aplicação: Representação de um percurso
Descarregar documentos do professor / alunoNesta aplicação da Unidade 6 irá ligar o TI-Innovator™ Rover utilizando a biblioteca TI Hub e construir um programa para registar as coordenadas dos pontos durante um percurso e, de seguida, representá-los graficamente.
Objetivos :
- Explorar o módulo TI Rover.
- Escrever e utilizar um programa para usar o TI-InnovatorTM Rover e os periféricos associados.
- Utilizar um ciclo fechado.
- Representar graficamente um conjunto de dados.

Passo 1
Nesta lição, iremos criar um programa que dará ao TI-Innovator™ Rover a capacidade de realizar um caminho correspondente ao desenho de um polígono regular.
As coordenadas dos vértices do polígono regular serão guardadas em listas e posteriormente representadas graficamente usando as instruções da biblioteca TI Plot.
IMPLEMENTAÇÃO DO PROGRAMA:
- Inicie um novo programa no editor de TI-Python, designe-o por U6AP.
- Selecione tipo de programa Codificação do Rover, desta forma automaticamente as bibliotecas bibliotecas TI Math, TI System e Time, serão importadas. Também o módulo TI PlotLib será importado para o programa agora iniciado.
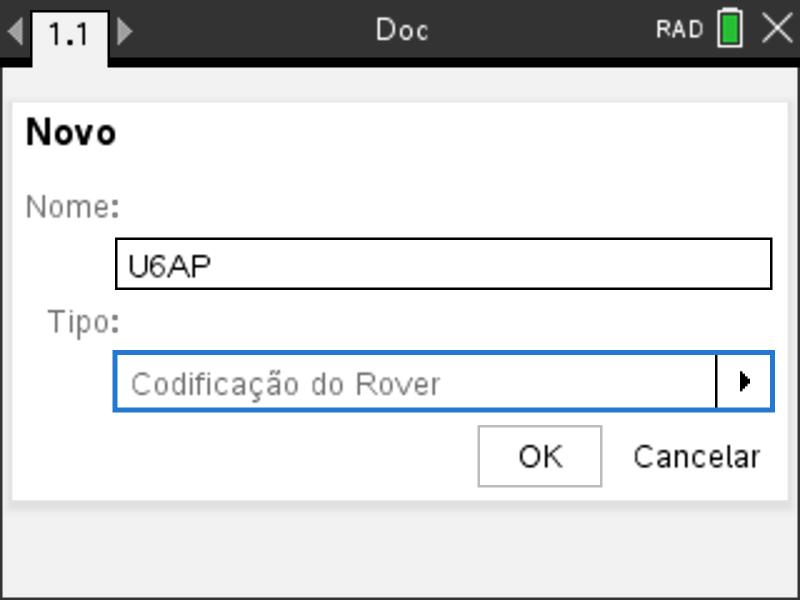
Passo 2
- Agora, poderá começar a escrever o programa.
- Embora possa não ser necessário, as instruções para limpar o ecrã e não mostrar o cursor são sempre mais agradáveis para o utilizador. Assim, colocaremos, sempre que nos parecer conveniente a instrução clear_history() localizada na biblioteca TI System.
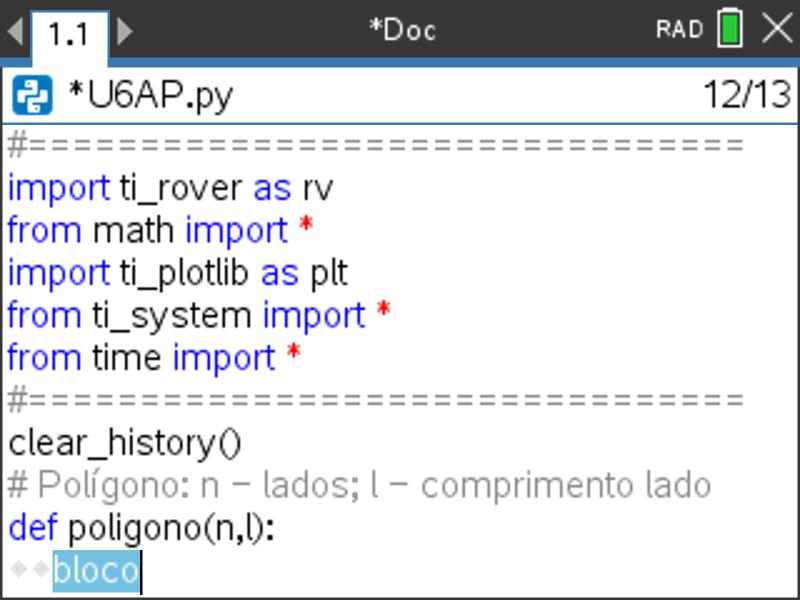
Passo 3
- Crie uma função poligono(), tomando como argumentos n o número de lados do polígono e l o comprimento, na unidade por defeito do TI-Innovator™ Rover, ou seja, o dm.
- A medida da amplitude do ângulo externo de cada polígono será, portanto, igual a = 360/n . Porquê o ângulo externo?
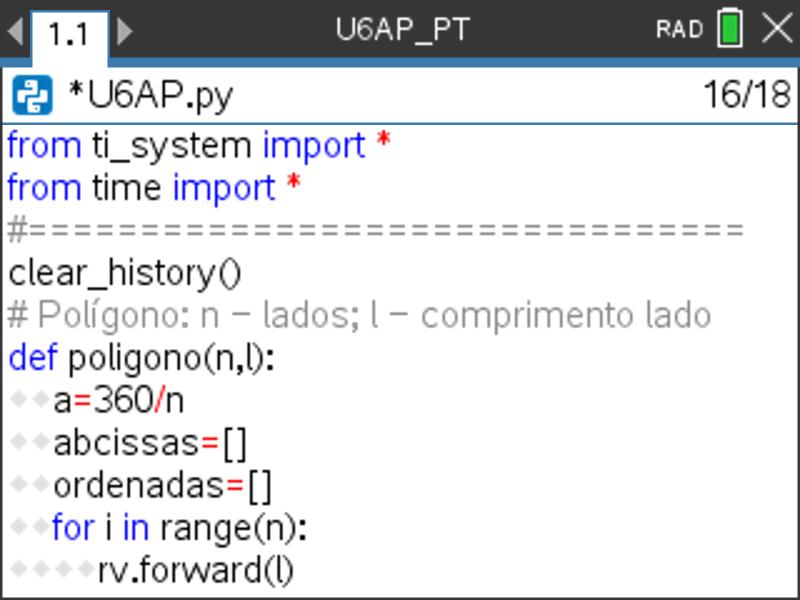
Passo 4
- Crie duas listas vazias, abcissas e ordenadas, destinadas a guardar as coordenadas de cada um dos n vértices.
- Crie um ciclo aberto, While, de tamanho n.
Passo 5
As instruções que se seguem, e que permitirão que o Rover percorra o percurso desenhado pelo polígono considerado, podem ser obtidas na biblioteca TI Rover. Estas instruções repetir-se-ão n vezes, tamanho do ciclo While.
- Mover para a frente o Rover em l decímetros – rv.foward(l).
- Virar à esquerda com um ângulo de amplitude a – rv.left(a).
- Colocar, entre cada etapa, uma espera de 1,5s – sleep(1.5).
- Obter e guardar as coordenadas dos vértices nas listas abcissas e ordenadas. – abcissas.append(rv.waypoint_x()) e ordenadas.append(rv.waypoint_x())
- Desconectar o Rover no final do percurso – rv._isconnect_rv().
- Exportar os dados das listas abcissas e ordenadas, respetivamente, para as listas lx e ly, possibilitando a representação gráfica e/ou exploração dos dados numa outra aplicação da TI-Nspire™ CX II (Gráficos, Listas e Folha de Cálculo, …).
Passo 6
OBSERVAÇÕES:
- As instruções rv.waypoint_x() e rv.waypoint_y() encontram-se no módulo TI Rover, na opção 5: Caminho, e de seguida a opção C: waypoint_x() .
- A instrução rv._isconnect_rv() deve ser escrita a partir do teclado.
- A instrução store_list() encontra-se no módulo TI System, na opção 5: store_list(“name”,list).
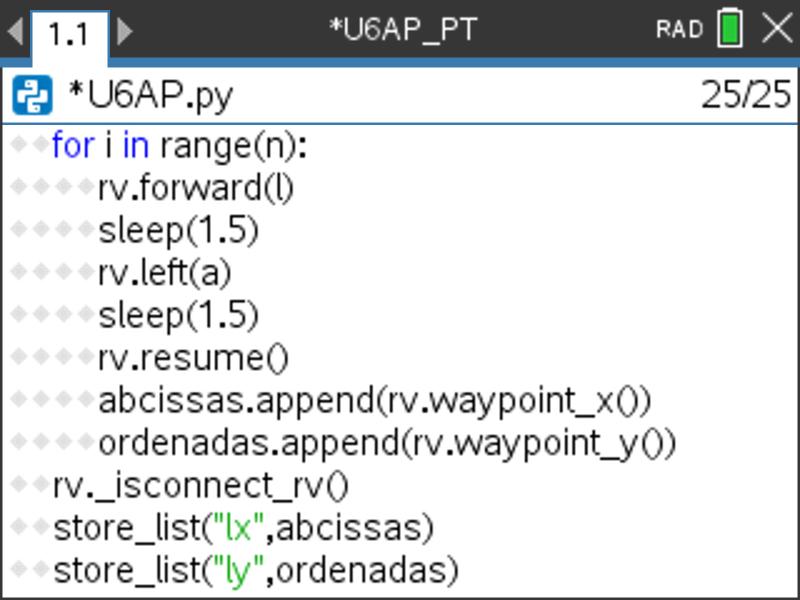
Passo 7
- Terminada a recolha de dados e o deslocamento do Rover, passemos para a representação gráfica dos dados. Podemos incluir este código na função já criada, ou, se for vantajoso, criar no mesmo programa uma nova função para a representação gráfica, como se procedeu em alguns exemplos das lições anteriores (Unidade 5).
- Todas as instruções usadas para a representação gráfica dos dados estão disponíveis no módulo TI PlotLib, que obrigatoriamente terá a sua biblioteca importada, nas opções 2: Configurar e 3: Desenhar.
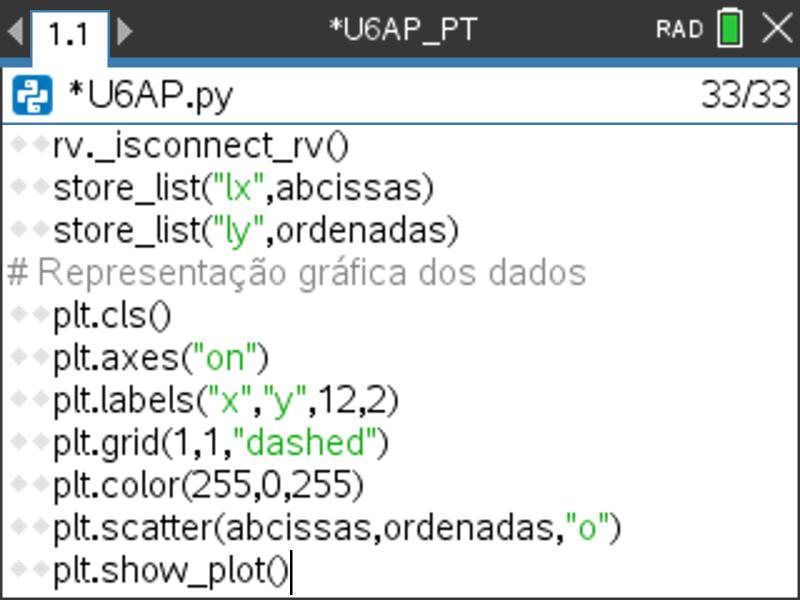
Passo 8
EXECUÇÃO DO PROGRAMA:
- Execute o seu programa, atalho
 , e, no interpretador, execute a função poligono() para, por exemplo, percorrer e desenhar um quadrado com o lado de comprimento 1 dm: poligono(4,1).
, e, no interpretador, execute a função poligono() para, por exemplo, percorrer e desenhar um quadrado com o lado de comprimento 1 dm: poligono(4,1). - Continue a testar o programa, agora com um hexágono regular com 2 dm de lado, poligono(6,2), obtendo a seguinte representação.
Passo 9
OBSERVAÇÃO:
Para este tipo de exercício, evite utilizar as instruções rv.pathlist_x() e rv.pathlist_y().
Pois, ao desenhar um segmento, serão registadas as coordenadas dos pontos de um segmento do polígono e, em seguida, no segmento seguinte serão registados novamente as coordenadas do último ponto do segmento anterior como o primeiro ponto do atual segmento.
Mais ainda, porque no nosso código colocamos um atraso de 1.5 s entre cada movimento do Rover. Portanto, as instruções rv.path… são, para o nosso caso, inapropriadas.
Usando as instruções rv.pathlist_x() e rv.pathlist_y(), obteríamos as coordenadas do ponto final duas vezes.Passo 10
NOTE QUE:
Deve ajustar o formato de sua grelha de fundo, dependendo dos polígonos que deseja desenhar. Isso foi intencionalmente definido aqui nas configurações por defeito, a fim de observar a precisão da pista do TI-Innovator™ Rover.
Também deve ter em atenção a natureza da superfície na qual o Rover se irá deslocar. O piso não deve oferecer muita resistência ao movimento ou, pelo contrário, favorecer o deslizamento.- Lição 1
- Lição 2
- Lição 3
- Aplicação
Unidade 7: Utilização da biblioteca Matemática Complexa
Lição 1: As funções da biblioteca cmath
Descarregar documentos do professor / alunoNesta primeira lição da Unidade 7, pode aprender como utilizar a biblioteca cmath (Matemática Complexa) para efetuar cálculos simples com números complexos.
Objetivos:
- Descobrir a biblioteca cmath.
- Utilizar as funcionalidades da biblioteca cmath.
Passo 1
- Utilizar o módulo cmath.
- Inserir uma nova aplicação e escolher o menu A: Adicione Python.
- Nesta lição, vamos trabalhar essencialmente com o interpretador (Shell) para tratar as instruções da biblioteca cmath.
- Na janela que se abre, escolher a opção 3: Shell.
- A tecla
 dá acesso a 9: Mais módulos, e depois a aceder a 1: Matemática complexa.
dá acesso a 9: Mais módulos, e depois a aceder a 1: Matemática complexa.
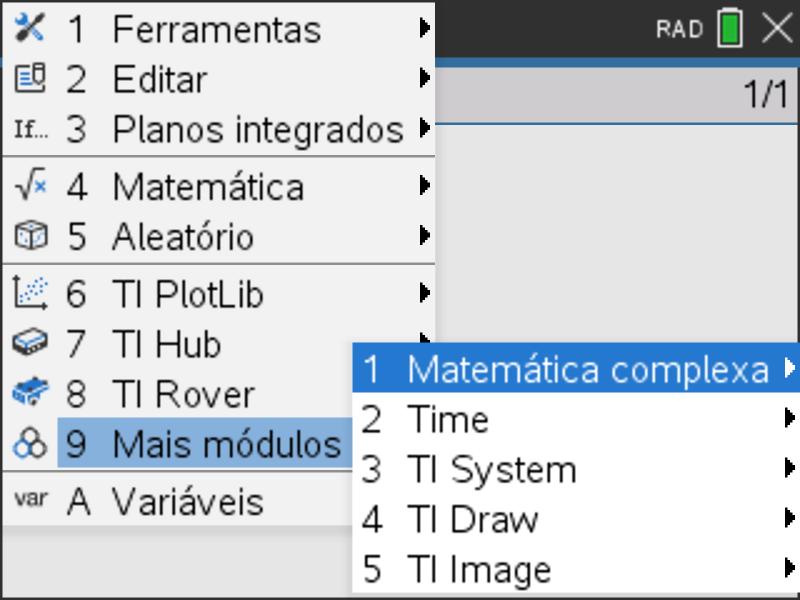
Passo 2
- Importar a biblioteca cmath.
- Escolher a opção 2: complex(real, imag) e atribuir este número a uma variável z.
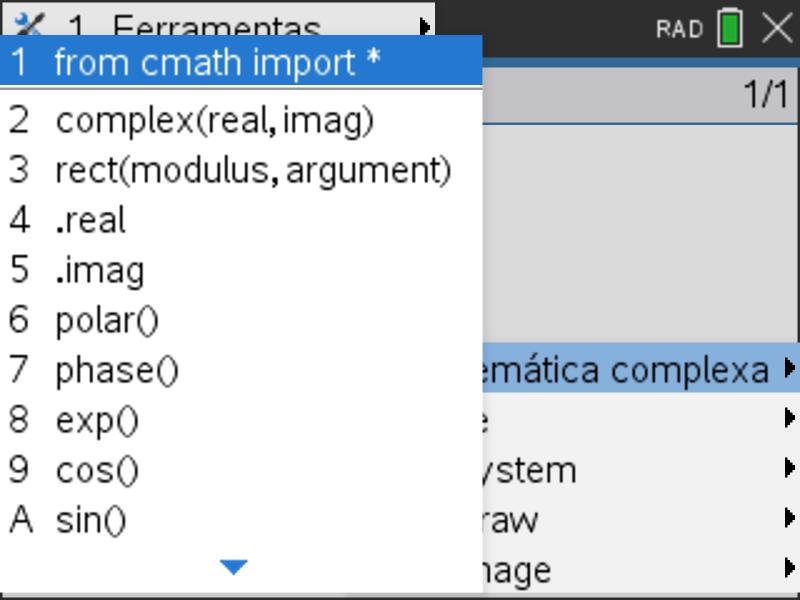
Passo 3
- Chamar a variável z.
- A calculadora utiliza j para designar a unidade imaginária.
Observe que o número complexo é apresentado entre parênteses na forma
z = a + bj
Da mesma forma, definir um número complexo sem usar a instrução complex(real, imag), mas diretamente utilizando a sintaxe, como por exemplo z2 = (2 - 3j)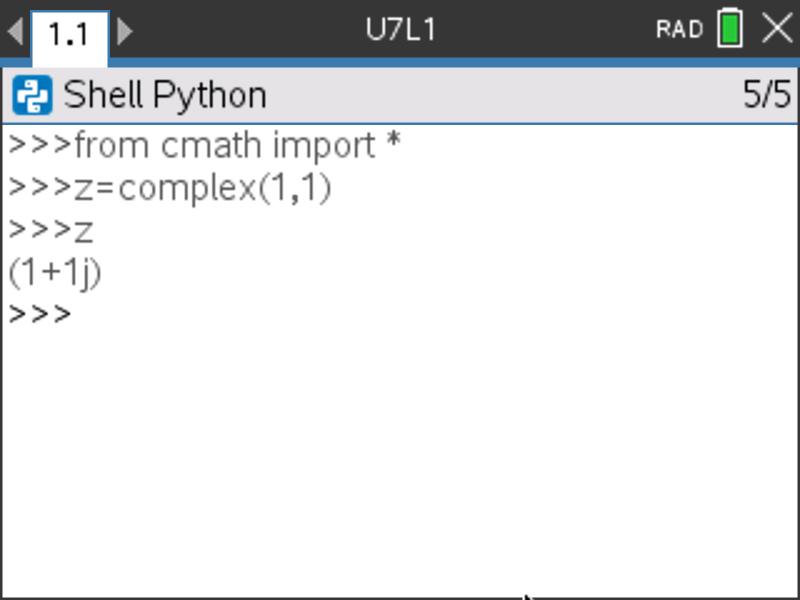
Passo 4
- Importar também na Shell a biblioteca de cálculos matemáticos.
- Na biblioteca cmath, escolher a instrução 3: rect(modulus, argument).
- Completar com a instrução rect(sqrt(2), pi/4), que dá origem à escrita em coordenadas cartesianas do número complexo de módulo √2 e argumento π/4.

Passo 5
- A exibição da parte real e do coeficiente da parte imaginária de um número complexo efetuam-se com .real e .imag precedido do nome da variável complexa.
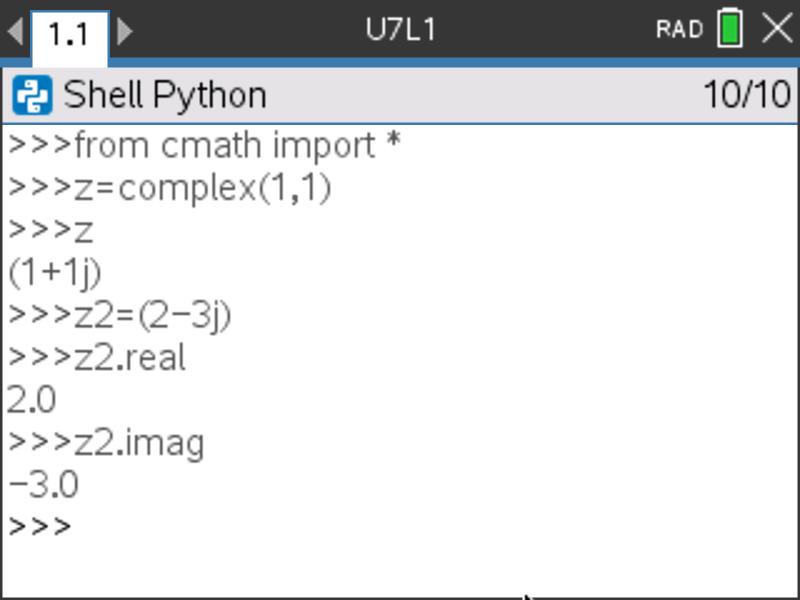
Passo 6
- A instrução 6: polar() deve conter como único argumento o nome da variável complexa para retomar um par ordenado cujo primeiro elemento será o módulo e o segundo o argumento do número complexo.
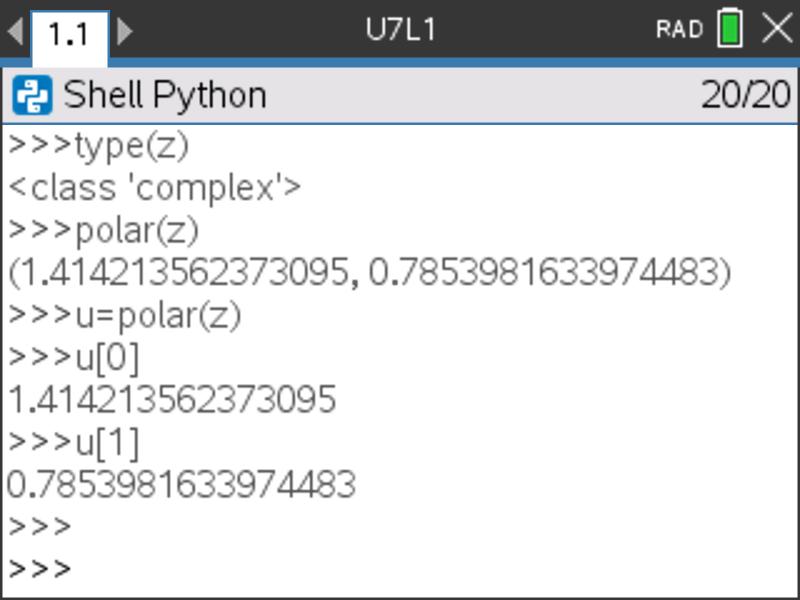
Passo 7
- A instrução 7: phase() dá o argumento, em radianos, do número complexo.
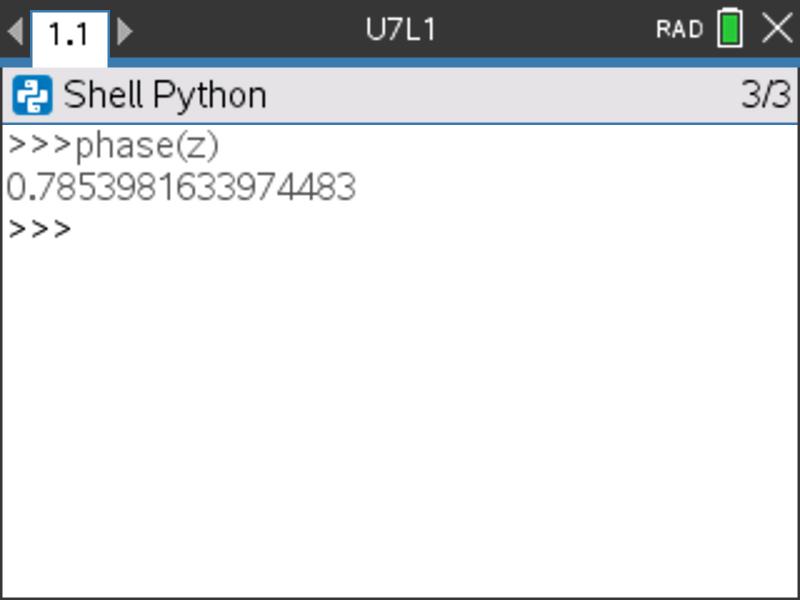
Passo 8
- Para obter o argumento de um número complexo em graus, utilizar a função degrees(), que está na biblioteca de funções matemáticas.
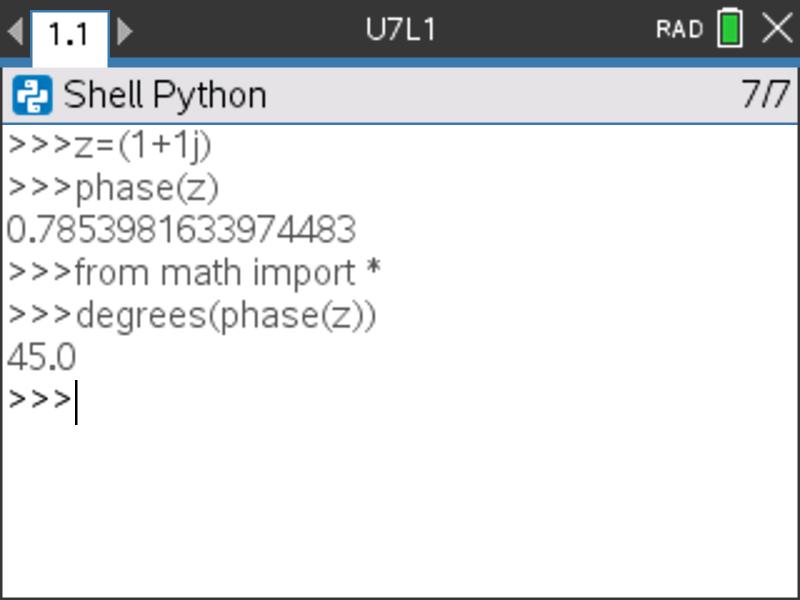
Passo 9
Quadrado de um imaginário puro.
- Criar o número complexo (preste atenção às instruções a dar à calculadora).
- Calcular
- Obtém-se o resultado esperado, tendo em consideração a forma como os decimais são expressos em linguagem Python.
- Pode escrever-se num programa uma função que atribua 0 à parte real ou imaginária de um número complexo quando o valor não ultrapassar 10−n, sendo n a precisão.
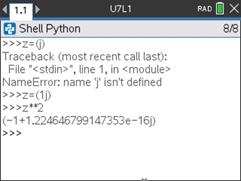
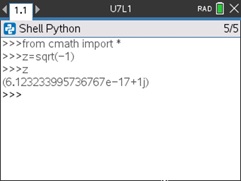
Passo 10
2. Alguns cálculos elementares
- Condições com números complexos.
Definir o número complexo com parte real 3 e coeficiente da parte imaginária 2. Verificar que o módulo deste número é √13
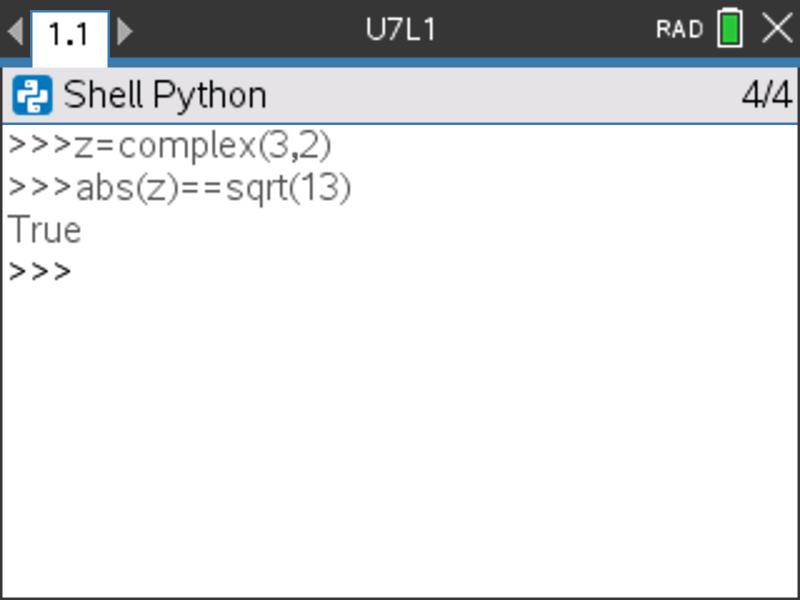
Passo 11
b) Conjugado de um número complexo.
O conjugado de um número complexo não é implementado na calculadora TI-Nspire™. Assim, propõe-se, para finalizar esta lição, a escrita de um programa que permita obter o conjugado de um número complexo dado.
- Inserir uma nova página com a aplicação TI-Python para escrita do programa e nomeie-se por U7L1.
- Importar as bibliotecas de cálculo matemático e o módulo cmath.
- Extrair as partes real e imaginária do complexo que é argumento da função definida.
- Exibir os dois números z e z.
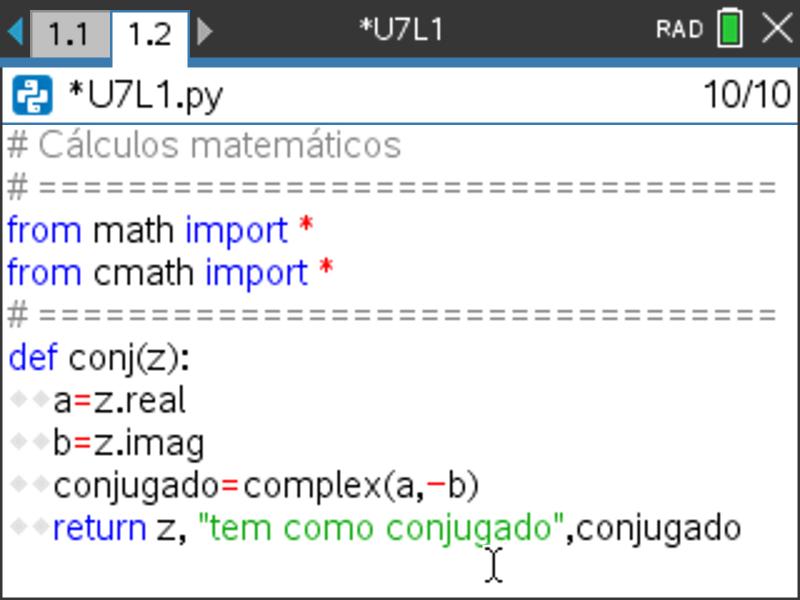
Lição 2: Cálculos e representações
Descarregar documentos do professor / alunoNesta segunda lição da Unidade 7, aprenderá a utilizar a biblioteca cmath (Matemática complexa) para efetuar cálculos simples com números complexos.
Objetivos :
- Utilizar a biblioteca cmath.
- Realizar cálculos com números complexos.
- Representar graficamente números complexos
Passo 1
- Iniciar um novo programa com o nome U7L2.
- Inserir uma nova aplicação, escolhendo no menu A: Adicionar Python.
- Com a tecla b aceder a 9: Mais módulos e depois 1: Matemática complexa.
Passo 2
- Criar uma função calcC(a,b,c,d) tendo como argumentos as partes reais e imaginárias dos números complexos: 𝑧1=𝑎+𝑏𝑗 e 𝑧2=𝑐+𝑑𝑗
- Usar esta função para obter o produto e o quociente dos dois números complexos, ou seja, z1 x z2 e z1 / z2 .
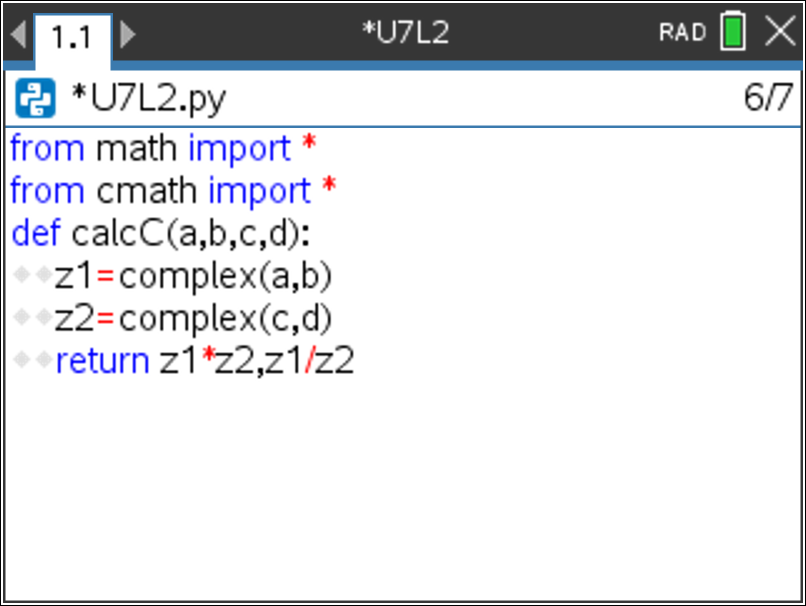
Passo 3
- Testar a função com dois números complexos à sua escolha.
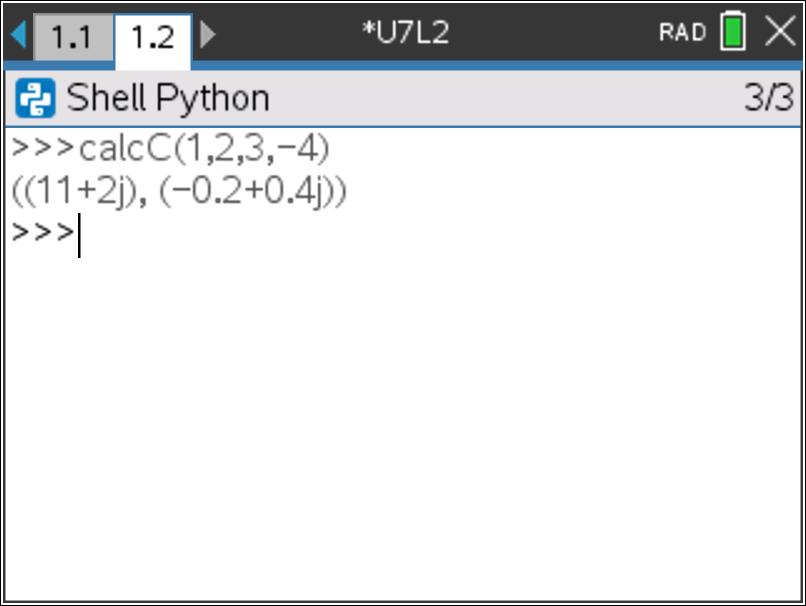
Passo 4
2. As diferentes formas de um número complexo.
Criará agora uma função que permita trabalhar de forma mais simples com números complexos usando formas trigonométricas ou exponenciais.
a) Forma trigonométrica e exponencial.
Escrever uma função para obter o módulo e o argumento de um número complexo (radianos e graus) para poder escrever na forma
𝑧 = 𝜌 × ( 𝑐𝑜𝑠𝜃 + 𝑗 𝑠𝑖𝑛𝜃) e depois 𝑧 = 𝜌 × ejθ.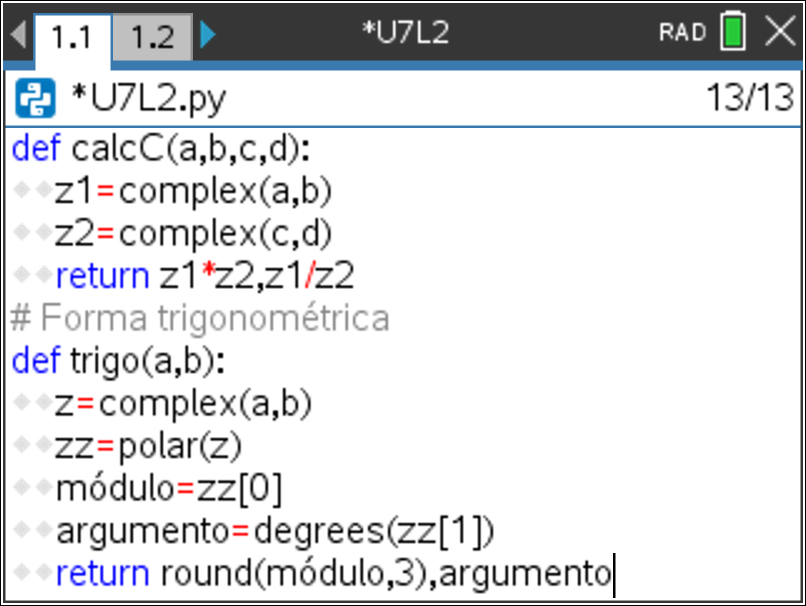
Passo 5
Estudo de um exemplo:
Considere o número complexo z = 4√3+4j
- Determinar o módulo e um argumento deste número complexo (mod 2π).
Dar a expressão na forma trigonométrica e depois exponencial.
A função permite rapidamente verificar que o número complexo tem módulo
𝜌 = 8 e argumento 𝜃 = 30° , ou (𝜋/6) mod 2𝜋.
A forma exponencial será 𝑧 = 8 × e j(π/6)
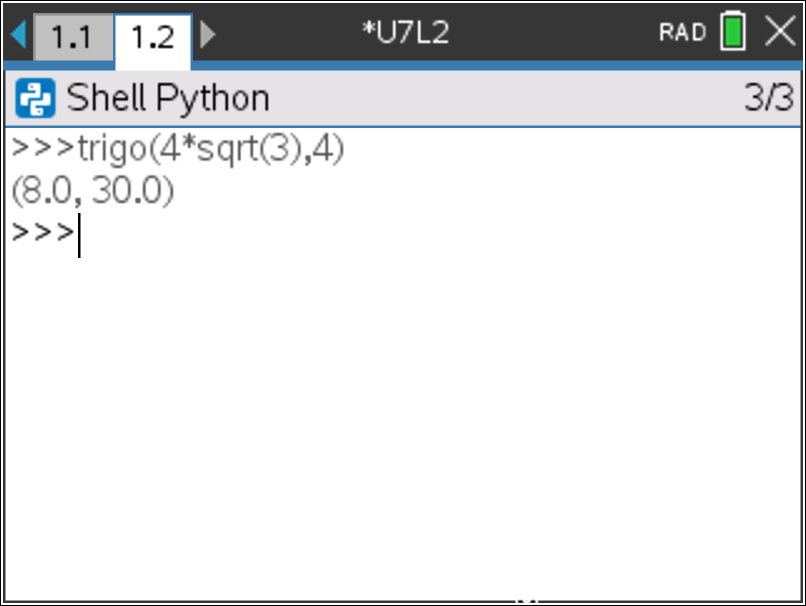
Passo 6
b) Interesse das formas trigonométricas e exponenciais.
Use as duas funções anteriores (ou crie outra que utilize as duas), para verificar que para dois números complexos:
- O módulo do produto é o produto dos módulos e o argumento do produto é a soma dos argumentos.
- O módulo do quociente é o quociente dos módulos e o argumento do quociente é a diferença dos argumentos.
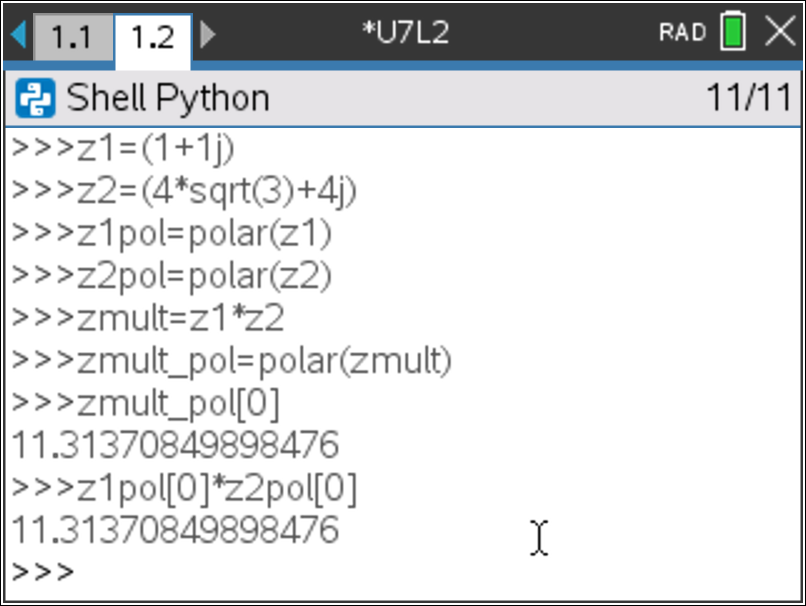
Passo 7
Estudo de um exemplo:
Considere os dois seguintes números complexo na forma algébrica:
z1 = 1 + 1j e z2 = 4√3 + 4j
De seguida use os operadores lógicos, mas tenha cuidado!
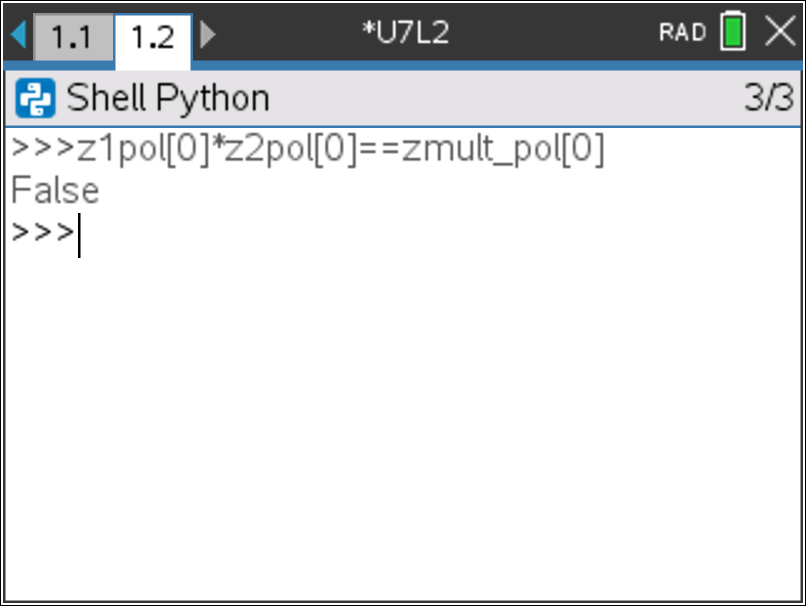
Passo 8
3. Representar graficamente um número complexo.
Represente num plano os números complexos anteriores:
z1 = 1 + 1j e z2 = 4√3 + 4j
Para tal, deve:
- Extrair as partes reais e imaginárias dos números complexos.
- Guardá-los em duas listas x[⬚ ] e y [⬚ ].
- Representar graficamente estas listas como nuvem de pontos.
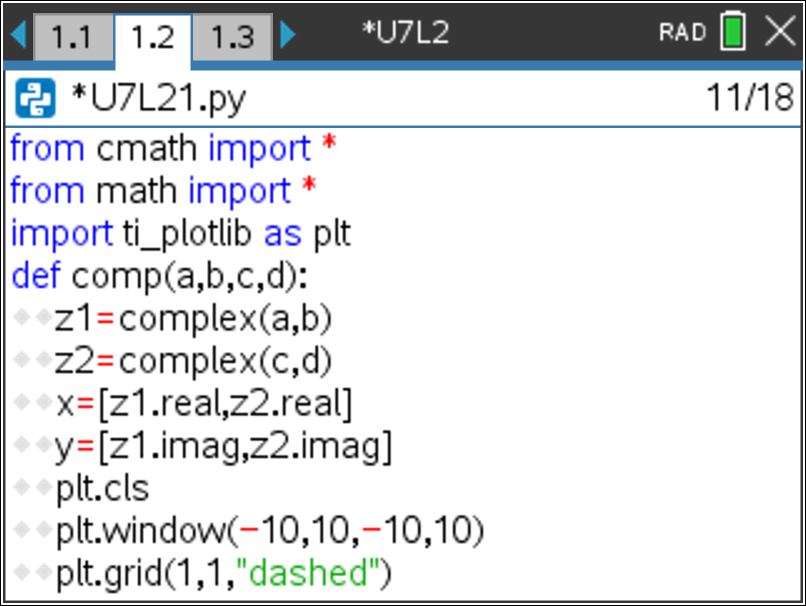
Passo 9
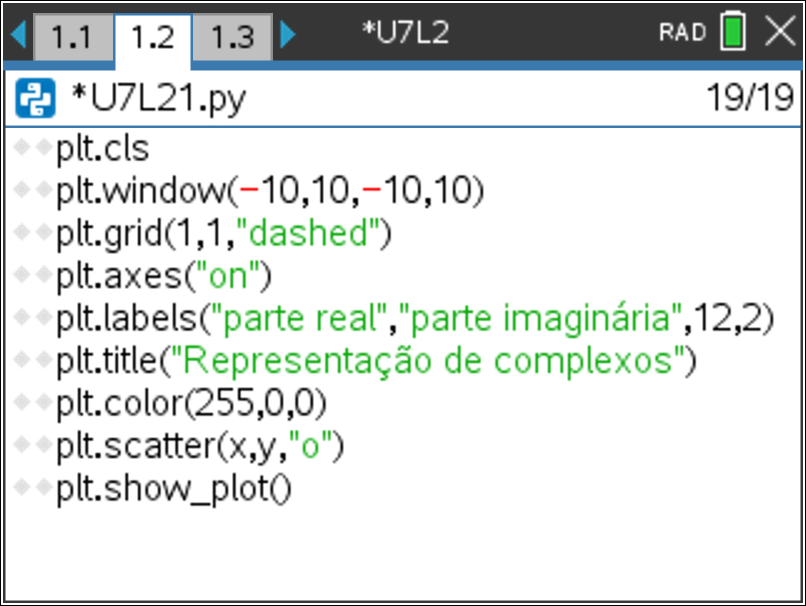
Passo 10
- Executar o programa.
- Solicitar a representação gráfica dos números complexos propostos.
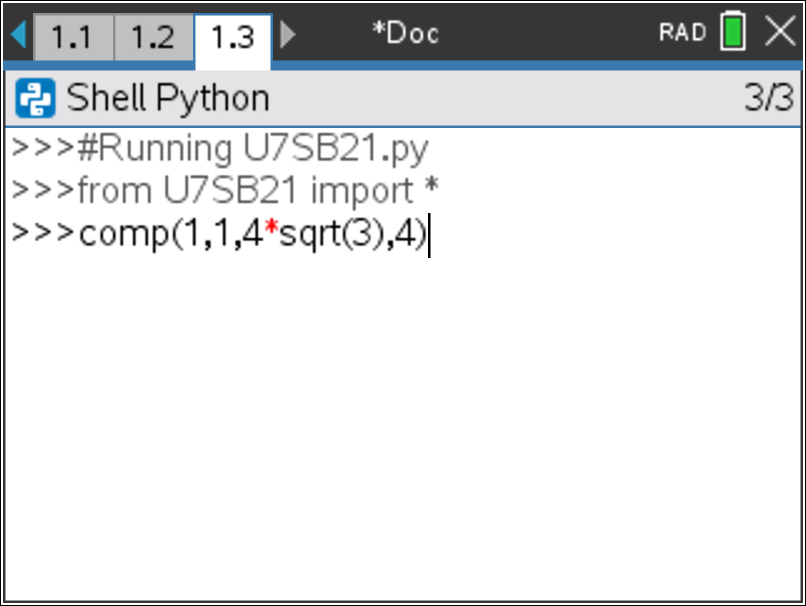
Lição 3: Representar números complexos
Descarregar documentos do professor / alunoNesta terceira lição da unidade 7, vai utilizar a biblioteca cmath (Matemática complexa) associada à biblioteca TI PlotLib para efetuar representações de números complexos.
Objetivos:
- Descobrir a biblioteca cmath.
- Utilizar as funcionalidades da biblioteca cmath
- Representar geometricamente números complexos.
Passo 1
Escrita complexa de uma transformação geométrica.
Uma transformação F faz corresponder a cada ponto M a sua imagem M’. Os pontos M e M’ consideram-se como afixos de números complexos, respetivamente z e z'.
A escrita complexa da transformação F é: z'= f (z), ou seja, f é a função de C → C que a z associa z'.
A escrita complexa de uma rotação de centro C, afixo de ω, e ângulo θ é:
z' = eiθ ( z - ω ) + ω
Determinar o afixo de zb, imagem do ponto A, afixo de za = 1 + 2j, pela rotação de ângulo (2π/3) e centro no afixo de ω = -1 + j.
Passo 2
- Iniciar uma nova aplicação, escolhendo A: Adicione Python.
- Criar um novo programa com o nome U7L3
- Na tecla menu b escolher a 9: Mais módulos, e depois 1 Matemática complexa.
- Inserir as bibliotecas math e cmath
Passo 3
- Vai criar uma função com 3 argumentos e que permite obter o afixo de zb = c + dj , imagem de um ponto A, afixo de za = a + bj, por uma rotação de ângulo θ em torno de C, afixo de ω.
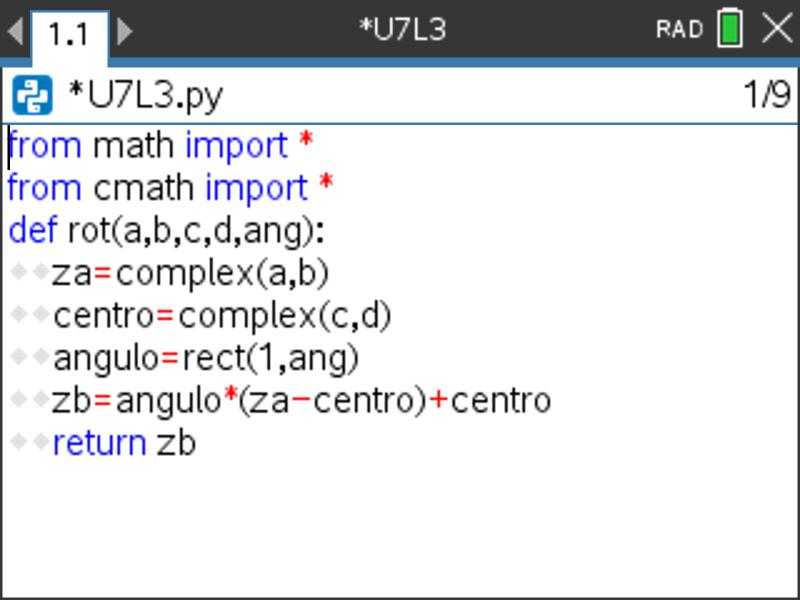
Passo 4
- Executar o programa.
- Verificar que o afixo de é:
zb = ( (-4 - √3) / ( 2 ) ) + ( ( 1 + 2√3 ) / ( 2 ) ) x ( j )
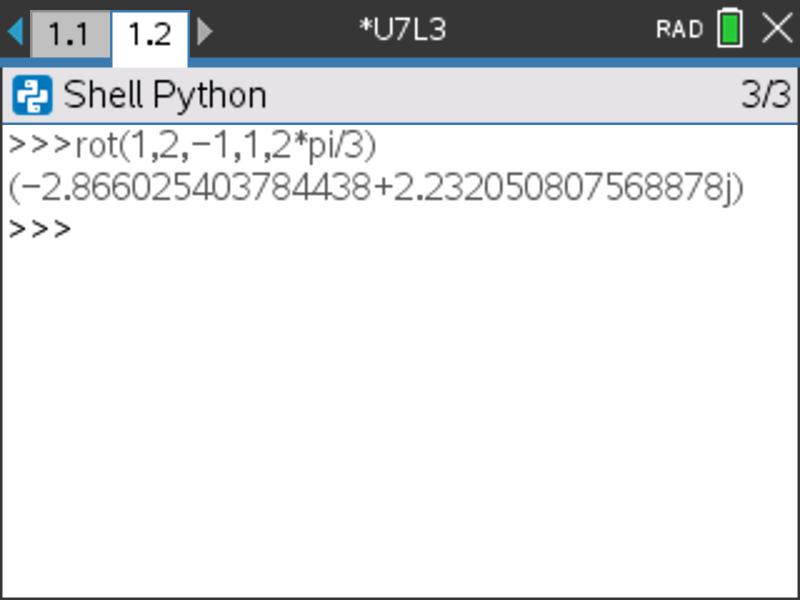
Passo 5
Transformação complexa e representação gráfica.
Agora vai utilizar rentabilizar a função anterior para mostrar que um triângulo é equilátero.
Sejam A(a,b), B(c,d), C(e,f) os afixos, respetivamente, de: za = √3 + 2 - 3j ; zb = - 2 e zc = 2√3 + 2 j √3 .
- Modificar o programa para que efetue a representação gráfica. Para tal, crie duas listas e contendo respetivamente as partes reais e os coeficientes das partes imaginárias dos complexos e.
- Representar graficamente os 3 pontos (nuvem de pontos).
- Utilizar a função rot( ) para mostrar, por exemplo, que o ponto A é imagem de C pela rotação r de centro B e ângulo -( π / 3 ).
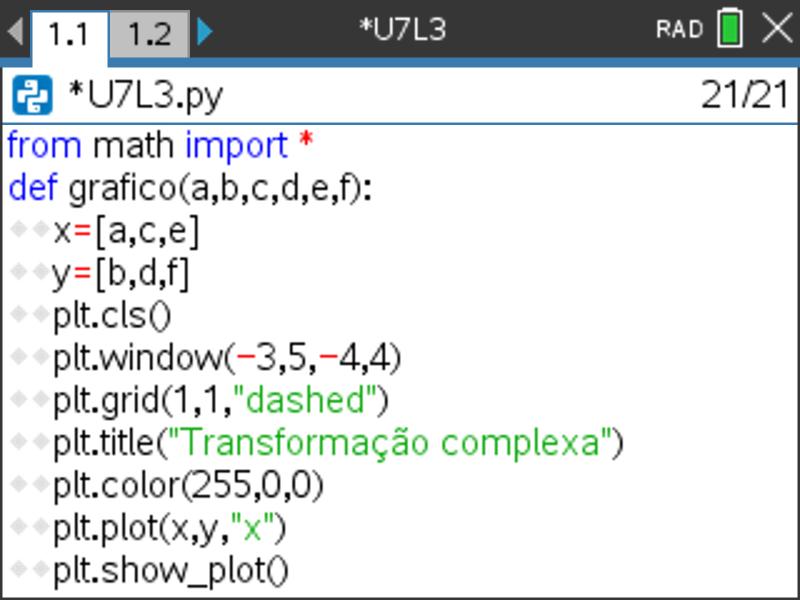
Passo 6
Donde c' = ( (1/2) - ( ( √3/2 ) j ) ) ( ( 2 √3 ) + ( 2 j √3 ) + ( 2 ) ) - 2 , ou seja c' = √3 + 1 + ( √3 j ) - ( j √3 ) + 3 - 2 ,
Logo c' = √3 + 2 - 3j .
A é imagem de C por r, que dá
BC = BA e ![]()
Aplicação: Números complexos e ciências
Descarregar documentos do professor / alunoNesta aplicação da unidade 7, irá utilizar a biblioteca cmath (Matemática complexa) para efetuar cálculos e representar números complexos utilizados na Física para o estudo de um circuito elétrico.
Objetivos :
- Descobrir a biblioteca cmath.
- Utilizar as funcionalidades da biblioteca cmath.
- Representar números complexos graficamente.
- Analisar um circuito elétrico RLC em série.
Passo 1
O circuito RLC em série.
Um circuito RLC em eletrónica é um circuito linear que contém um resistor (R), um indutor (L) e um condensador (C).
Há dois tipos de circuitos RLC, em série ou paralelo, de acordo com a ligação dos três componentes. O comportamento de um circuito RLC é em geral descrito por uma equação diferencial de segunda ordem (ou circuitos RL ou RC modelados por equações diferenciais de primeira ordem).
Usando um gerador de sinais, podemos injetar oscilações no circuito e observa rem alguns casos uma ressonância, caracterizada por um aumento na corrente (quando o sinal de entrada selecionado corresponder à própria pulsação do circuito, calculável pela equação diferencial que o contempla).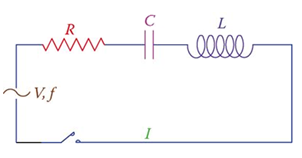
Passo 2
Num dipolo linear, não necessariamente elementar, mas constituído por um conjunto de elementos lineares passivos R,L,C se tomarmos a equação que liga a tensão à corrente e aplicarmos uma tensão
![]() , obteremos uma corrente
, obteremos uma corrente ![]() . Chamamos impedância complexa do dipolo a quantidade:
. Chamamos impedância complexa do dipolo a quantidade:
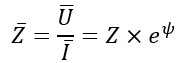
Qual é a utilidade da noção de impedância?
Se conhecermos o módulo de Z e um argumento φ do dipolo, podemos imediatamente passar da tensão à corrente e reciprocamente: o módulo de Z indica a relação entre a tensão e a corrente.
Um argumento φ fornece a mudança de fase entre a tensão e a corrente.
ω representa a pulsação (frequência angular) do sinal elétrico ; f
Lembra-se que ω = 2 π f ; f é a frequência do sinal, expressa em (Hz).Passo 3
Impedância complexa.
Resistor de resistência R: Z = R
Indutor L: Z = jlω
Condensador (capacitador) C: Z =( 1 / jCω ) ou bien Z =( -j / Cω )

Passo 4
Estudo de um exemplo.
- Criar um programa em Python para determinar a impedância complexa de um circuito RLC em série.
- Representar graficamente a impedância de cada dipolo e depois a impedância total.
- Deduzir a natureza do circuito (dominante indutiva ou capacitiva).
Passo 5
- Inserir uma nova aplicação com o menu A Adicione Python.
- Criar um novo programa com o nome U7AP.
- Importar as bibliotecas math e cmaths.
- Criar uma função com 3 argumentos, os quais são os valores das impedâncias de cada dipolo, na ordem ZR, ZL e ZC.
- A função deverá determinar a impedância complexa total, o módulo da impedância total e um argumento, arredondado à décima do grau.
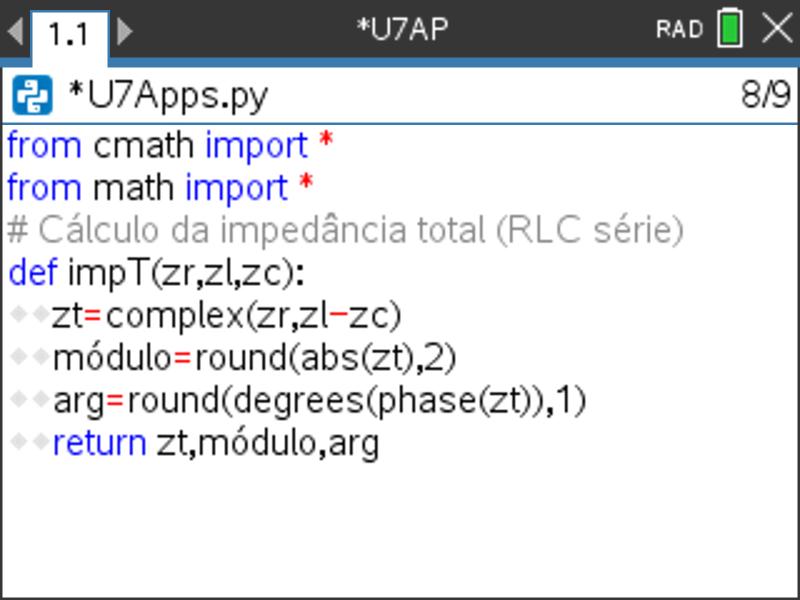
Passo 6
- Executar o programa e determinar a impedância total dum circuito RLC em série, tal que:
𝑧𝑟 = 2Ω ; 𝑧𝑙 = 3Ω ; zc = 1Ω
- A fase é de 45°, o comportamento do circuito é predominantemente indutivo.
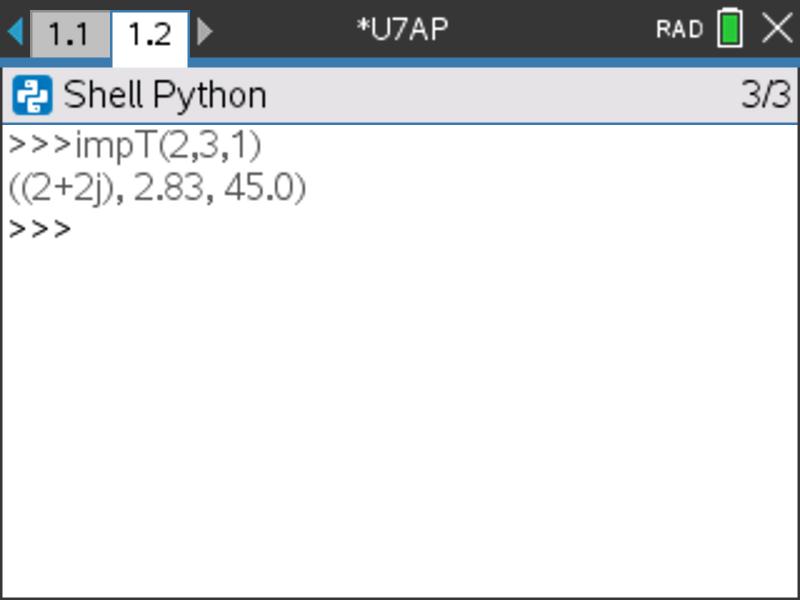
Passo 7
Representar graficamente o diagrama de impedâncias.
- Trata-se de representar no plano a soma de três vetores. Na eletricidade, uma prática comum consiste em representar a partir da origem o vetor Ur(zr, 0) e depois, a partir da sua extremidade, o vetor Ul (zl. π/2 ) e finalmente, também a partir da extremidade, o vetor Uc = ( zc, (- π/2 ) .
- Importe as bibliotecas TI PlotLib para o programa. Modifique-o para que forneça o valor da impedância complexa após a representação gráfica. Pressionando a tecla . irá parar a representação gráfica.
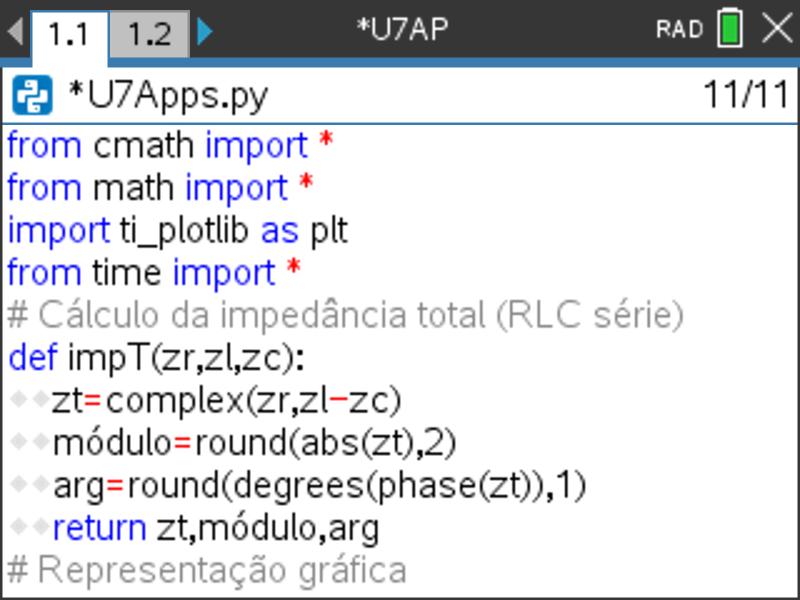
Passo 8
- O vetor correspondente à impedância total terá cor magenta, conseguindo-se com a instrução plt.color(255,0,255).
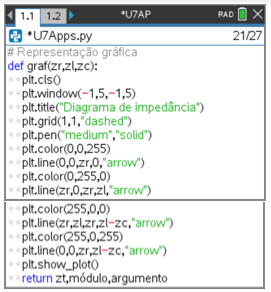
- Lição 1
- Lição 2
- Lição 3
- Aplicação