Texas Instruments
9-12
60 Minutes
TI-Nspire™TI-Nspire™ CAS
2.0
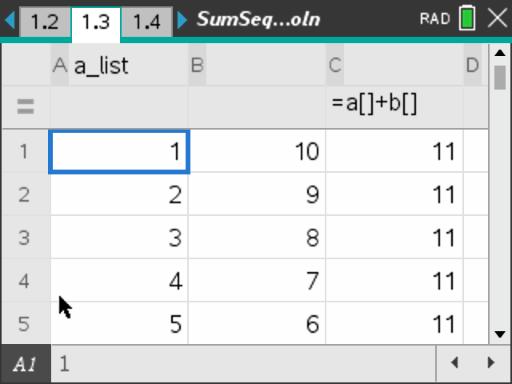
In this activity, students will develop formulas for the sum of arithmetic and geometric sequences. Students will then find the sum of sequences using the formulas developed.
In this activity, students will first perform a numerical process/proof to find the sum of an arithmetic sequence. To do this, they will be entering the sequence in reverse order and finding the sums of the rows.
After students develop a formula for the sum of an arithmetic sequence, they will apply the formula.
In the second part of the activity, students develop the formula for the sum of a geometric sequence. To do this, they will multiply each term in the sequence by the common ratio, find the difference between the two different values, and divide by a value to determine the sum of column A.
TI websites use cookies to optimize site functionality and improve your experience. To find out more or to change your preferences, see our cookie policy page. Click Agree and Proceed to accept cookies and enter the site.
You can control your preferences for how we use cookies to collect and use information while you're on TI websites by adjusting the status of these categories.