Exploring the Equation of a Circle
Exploring the Equation of a Circle
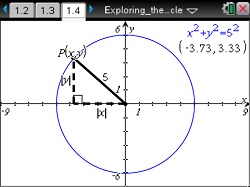
Explore right triangles and the Pythagorean Theorem to develop the equation of a circle.
- Students will understand the definition of a circle as a set of all points that are equidistant from a given point.
- Students will understand that the coordinates of a point on a circle must satisfy the equation of that circle.
- Students will relate the Pythagorean Theorem and Distance Formula to the equation of a circle.
- Given the equation of a circle (x – h)2 + (y – k)2 = r 2, students will identify the radius r and center (h, k).
- Pythagorean Theorem
- Distance Formula
- Radius
This lesson involves plotting points that are a fixed distance from the origin, dilating a circle entered on the origin, translating a circle away from the origin, and dilating and translating a circle while tracing a point along its circumference. As a result students will:
- Visualize the definition of a circle.
- Visualize the relationship between the radius and the hypotenuse of a right triangle.
- Observe the consequence of this manipulation on the equation of the circle.
- Infer the relationship between the equation of a circle and the Pythagorean Theorem.
- Infer the relationship between the equation of a circle and the Distance Formula.
- Identify the radius r and center (h, k) of the circle (x −h)2 + (y − k)2 = r 2.
- Deduce that the coordinates of a point on the circle must satisfy the equation of that circle.
Vernier EasyData,Vernier EasyLink and Vernier EasyTemp are registered trademarks of Vernier Science Education.

