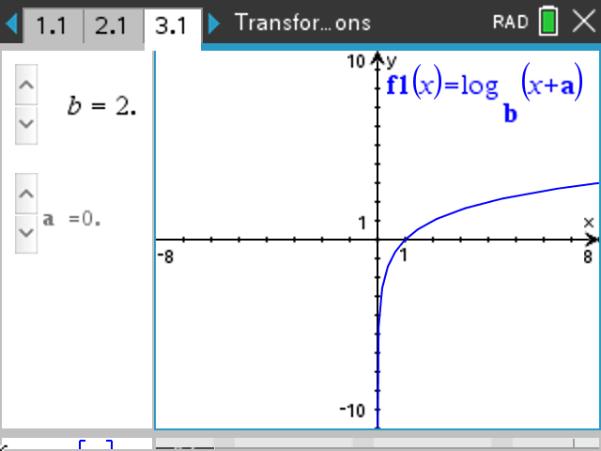
This lesson involves the family of logarithmic functions of the form f(x) = c*log_b(x+a).

• Students will explore the family of logarithmic functions of the form f(x) = c*log_b(x+a) and describe the effect of each parameter on the graph of y = f(x)
• Students will determine the equation that corresponds to the graph of a logarithmic function.
• Students will understand how a vertical shift in the graph of a logarithmic function is related to properties of logarithmic functions.

• logarithmic function
• natural logarithm
• parameter
• translation
• reflection

This lesson involves the family of logarithmic functions of the form f(x) = c*log_b(x+a).

As a result, students will:

• Manipulate minimized sliders, and observe the effect on the graph of the corresponding logarithmic function.
• Make a general statement about the effect of each parameter on the graph of the logarithmic function.
• Match specific logarithmic functions with their corresponding graphs.
• Relate properties of logarithmic functions to vertical translations of their graphs.

*Note: This activity contains an optional AP Practice Questions document for those students preparing for the AP Precalculus Exam.