Pode estudar equações lineares e não lineares e sistemas de equações diferenciais ordinárias (EDOs), incluindo modelos logísticos e equações Lotka-Volterra (modelos predador-presa). Pode também marcar o campo vetorial com implementações interativas do método Euler e Runge-Kutta.
|
|
Linha de entrada EDO:
|
||||||||||||
|
|
Seletor para variar o coeficiente k da EDO |
||||||||||||
|
|
Campo vetorial |
||||||||||||
|
|
Uma curva solução que passa pela condição inicial |
Para representar graficamente uma equação diferencial:
| 1. | No menu Introdução/Edição do gráfico, selecione Eq. dif. |
É automaticamente atribuído um identificador à EDO, como “y1.”
| 2. | Mova para o campo da relação e introduza a expressão que define a relação. Por exemplo, pode introduzir -y1+0.1*y1*y2. |
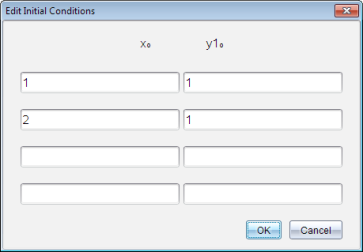
| 3. | Introduza a condição inicial para o valor independente x0 e para y10. |
Nota: Os valores x0 são comuns a todas as EDOs num problema mas só podem ser introduzidos ou modificados na primeira EDO.
| 4. | (Opcional) Para estudar várias condições iniciais para a EDO atual, clique em Adicionar condições iniciais  e introduza as condições. |
| 5. | Toque em Editar parâmetros  para definir os parâmetros do gráfico. Selecione um Método de solução numérico e, em seguida, defina parâmetros adicionais. Pode alterar esses parâmetros a qualquer altura. |
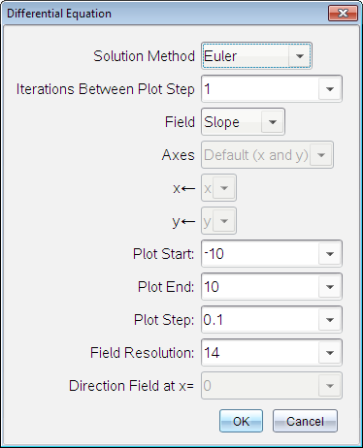
| 6. | Clique em OK. |
| 7. | Para introduzir EDOs adicionais, prima a seta para baixo para apresentar o próximo campo de edição de EDO. |
Quando se move entre EDOs definidas, o gráfico é atualizado de forma a refletir todas as alterações. Uma solução para a EDO é representada graficamente para cada IC especificado e para cada EDO apresentada (selecionada pela caixa de verificação).
Resumo das definições da equação diferencial
|
Método de solução |
Seleciona Euler ou Runge-Kutta como o método de solução numérica. |
|||||||||
|
Iterações entre passo de gráfico |
Precisão computacional apenas para método de solução Euler. Tem de ser um valor inteiro >0. Para restaurar a predefinição, selecione a seta para baixo e selecione Predefinição. |
|||||||||
|
Tolerância de erro |
Precisão computacional apenas para método de solução Runge-Kutta. Tem de ser um valor em vírgula flutuante |1×10-14. Para restaurar a predefinição, selecione a seta para baixo e selecione Predefinição. |
|||||||||
|
Campo |
Nenhum - Nenhum campo marcado. Disponível para qualquer número de EDOs, mas necessário se três ou mais EDOs de primeira ordem estiverem ativas. Coloca em gráfico uma combinação da solução e/ou valores de uma ou mais ODEs (de acordo com as definições dos Eixos configuradas pelo utilizador). Inclinação - Marca um campo que representa a família de soluções para uma única ODE de primeira ordem. Tem de estar uma ODE ativa. Define Eixos para Predefinição (x e y). Define o eixo horizontal para x (a variável independente). Define o eixo vertical para y (a solução para a EDO). Direção – Representa graficamente um campo no plano de fase que representa a relação entre uma solução e/ou valores de um sistema de duas EDOs de primeira-ordem (conforme especificado pela definição Eixos personalizados). Têm de estar duas ODEs activas. |
|||||||||
|
Eixos |
Predefinição (x e y) - Marca x no eixo x e y (as soluções para as equações diferenciais ativas) no eixo y. Personalizado - permite selecionar os valores a marcar no eixo x e y, respetivamente. As entradas válidas incluem:
|
|||||||||
|
Início da marcação |
Define o valor da variável independente, no qual a marcação da solução é iniciada. |
|||||||||
|
Fim da marcação |
Define o valor da variável independente, no qual a marcação da solução termina. |
|||||||||
|
Passo de marcação |
Define o incremento da variável independente, no qual os valores são marcados. |
|||||||||
|
Resolução do campo |
Define o número de colunas dos elementos de composição de campo (segmentos de reta) utilizados para desenhar um campo de vetores. Só pode alterar este parâmetro se Campo = Direção ou Inclinação. |
|||||||||
|
Campo de vetores em x= |
Define o valor da variável independente, no qual é desenhado um campo de vetores ao marcar equações não autónomas (aquela que se referem a x). Ignorado ao marcar equações autónomas. Só pode alterar este parâmetro se Campo = Direção. |