Symmetric Secant
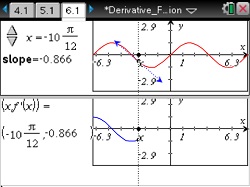
Symmetric Secant
Investigate the symmetric secant line to provide an estimate for the derivative of a function at a point.
- Use the slope of the symmetric secant line to approximate the derivative of a function at a point and generalize properties of functions that affect the accuracy of these estimates
- Explain the relationship between the symmetric difference quotient and the standard difference quotient used to calculate the derivative of a function at a point both graphically and numerically
- secant and tangent line
- difference quotient
- derivative
This lesson provides a visual demonstration of how and when the symmetric secant line can be used to provide a reasonable estimate for the derivative of a function at a point. As a result, students will:
- Explore a variety of function graphs to observe how the slope of the symmetric secant line comes closer to approximating the slope of the tangent line as the value of h decreases.
- Use the symmetric secant line to estimate derivatives at a point and compare these estimates to other numerical and analytic methods.
- Discover the importance of considering the function graph when estimating derivatives by exploring instances in which the symmetric difference quotient provides a value even though the derivative of the function does not exist.
Vernier EasyData,Vernier EasyLink and Vernier EasyTemp are registered trademarks of Vernier Science Education.

