Transformations: Rotations
Transformations: Rotations
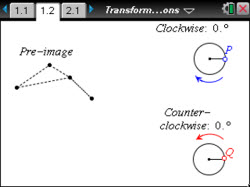
Explore clockwise and counterclockwise rotations to discover the properties of the pre-image and image of a triangle.
- Students will identify a rotation as an isometry, also called a congruence transformation.
- Students will identify which properties (side length, angle measure, perimeter, area, and orientation) of a figure are preserved in a rotation and which are not.
- Students will describe the relationship between the sign of the angle and the direction of rotation.
- Students will identify coordinates of an image that is rotated about the origin through angles of ±90°, ±180°, ±270°, and ±360°.
- Students will generalize the relationship between the coordinates of a pre-image and its image in a rotation about the origin in the coordinate plane.
- Look for and make use of structure. (CCSS Mathematical Practice)
- Look for and express regularity in repeated reasoning. (CCSS Mathematical Practice)
- pre-image
- image
- transformation
- rotation
- clockwise / counterclockwise direction
- congruent figures
- congruence transformation
- isometry
- positive and negative angles
In this lesson students will investigate the meaning of a rotation, and they will discover which properties are preserved in a rotation and which are not. They will identify and generalize the coordinates of a triangle under rotations in the coordinate plane.
As a result students will:
- Rotate a triangle in clockwise and counterclockwise directions to develop their visualization and special sense of a rotation.
- Describe the consequences of the rotation in terms of identifying those properties which are preserved and those which are not, and identify and generalize the coordinates of rotations in the coordinate plane.
- Infer that a rotation does not alter any of the measurements of a rotated object and, as such, a rotation is an example of an isometry, or congruence transformation.
Vernier EasyData,Vernier EasyLink and Vernier EasyTemp are registered trademarks of Vernier Science Education.

