In this activity, students will learn four characteristics of a normal curve: the distribution is symmetric and mound-shaped; the mean and median are approximately equal; the distribution meets the 68-95.5-99.7 rule; and the normal probability plot is linear. They will use these to determine if a data set it normal.

• Students will recognize that there are four tests for assessing normality in a data set:
  1. The distribution is mound-shaped and approximately symmetric.
  2. The mean and median are approximately equal.
  3. The distribution follows the 68-95-99.7 rule.
  4. A normal probability plot of the data set is approximately linear.
• Students will use the four tests to assess the normality of a given data set.

• normal distributions
• histograms
• measures of central tendency
• percentiles
• normal probability plot
• 68-95-99.7 rule

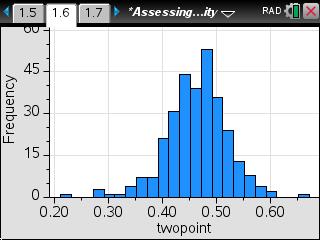
This lesson involves examining NBA two-point shooting percentages.
As a result, students will:

• Create a histogram of the data and determine if the shape meets the requirement for normality—mound-shaped and symmetric.
• Use one-variable statistics to find the mean and median and determine if they are approximately equal.
• Make a new histogram of the data using the mean as a cut-point and the standard deviation as the bin width. They will calculate the percentage of data values within one-, two- and three-standard deviations of the mean to determine if the histogram meets 68-95-99.7rule.
• Create a normal probability plot of the data and decide if the plot is linear, indicating normality.
• Summarize the results of all four tests to decide if the data set is approximately normal.