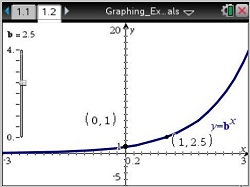
Investigate the graphs of the family of exponential functions.

• Infer why the conditions b > 0 and  b ≠ 0 are necessary for the function to be exponential
• Determine that for x > 1 the function is increasing and for 0 < x < 1 the function is decreasing
• Determine that the y-intercept is always (0,1) and there is no x-intercept
• Determine that for b > 1 the function approaches infinity as x approaches infinity and that for 0 < b < 1 the function approaches infinity as x approaches -infinity
• Identify the domain as (-infinity, inifinity) and the range as (0, infinity)
• Identify the equation of the function’s horizontal asymptote as y = 0

• Exponential function
• End behavior
• Intercepts
• Domain and range
• Asymptotes
• Increasing and decreasing functions

Students will investigate the graphs of the family of exponential functions f(x) = b^x. As a result, students will:

• Infer why the conditions b > 0 and b ≠ 0 are necessary.
• Determine how the value of b affects the increasing or decreasing behavior of the function.
• Determine the y-intercept, domain, and range.
• Describe the end behavior.
• State the equation of the asymptote.