Proof of Identity
Math: Algebra II: Trigonometric Functions
9-12
45 Minutes
TI-84 series
Lessons
Proof of Identity
Activity Overview
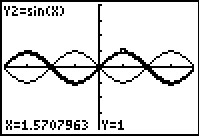
Students use graphs to verify the reciprocal identities. They then use the calculator's manual graph manipulation feature to discover the negative angle, cofunction, and Pythagorean trigonometric identities.
Download Files
Teacher Files
Student Files
Math: Algebra II: Trigonometric Functions
9-12
45 Minutes
TI-84 series
Lessons
iPad is a trademark of Apple Inc., registered in the U.S. and other countries.
Vernier EasyData,Vernier EasyLink and Vernier EasyTemp are registered trademarks of Vernier Science Education.
Vernier EasyData,Vernier EasyLink and Vernier EasyTemp are registered trademarks of Vernier Science Education.

