Activities

Objectives

• Students will recognize that the mean and standard deviation (SD) and the median and interquartile range (IQR) are two ways to measure center and spread.
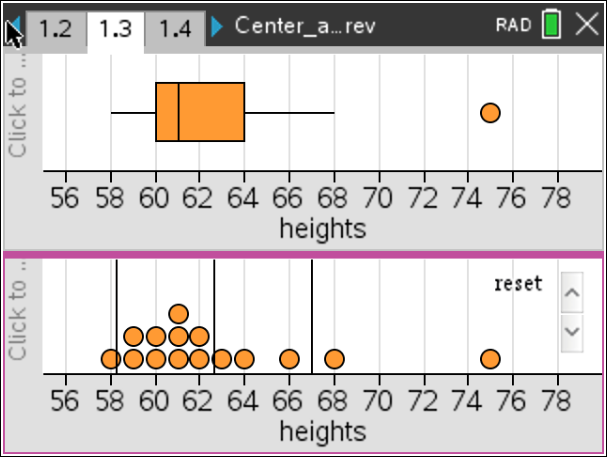
• Students will recognize that in a skewed distribution the mean is pulled in the direction of the tail, and the standard deviation is increased; in a distribution with an outlier, the mean is pulled in the direction of the outlier, and the standard deviation is increased.
• Students will be able to illustrate that the median and IQR are resistant to skewness/outliers while the mean and standard deviation are not.
• Students will recognize that the median and IQR are preferred when a distribution is skewed while either mean and SD or median/IQR are acceptable for approximately symmetric distributions.

Vocabulary

• Bimodal or unimodal
• Interquartile range
• Mean, median, and standard deviation
• Outlier
• Resistant
• Akewed or symmetric distribution

About the Lesson

This lesson involves moving points on dotplots. Students will:

• change the shape of the distribution and notice the effect on the mean and median and on the standard deviation and IQR.
• drag points to compare the effect of outliers on the mean/standard deviation and median/IQR.
• make and justify a conjecture about which measures are preferred based on the shape of the distribution.