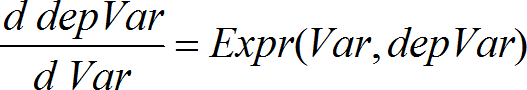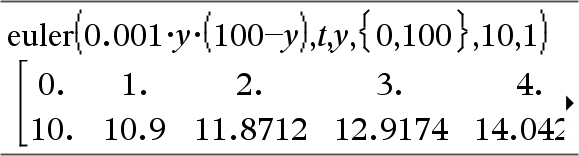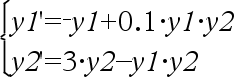|
u-toets |
|
|
e^(Waarde1)Þwaarde Geeft e tot de macht Waarde1. Opmerking: zie ook e macht-template, hier. Opmerking: op u drukken om e^( weer te geven is niet hetzelfde als drukken op het teken E op het toetsenbord. U kunt een complex getal in rei q polaire vorm invoeren. Gebruik deze vorm echter alleen in de hoekmodus Radialen; hij veroorzaakt een domeinfout in de hoekmodi Graden en Decimale graden. |
|
|
e^(Lijst1)Þlijst Geeft e tot de macht van elk element in Lijst1. |
|
|
e^(vierkanteMatrix1)ÞvierkanteMatrix Geeft de 'e tot de macht van vierkanteMatrix1'. Dit is niet hetzelfde als het berekenen van e tot de macht van elk element. Zie voor informatie over de berekeningsmethode cos(). vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma. |
|
|
Catalogus > |
|
|
eff(nominaalPercentage,CpY)Þwaarde Financiële functie die het nominale rentepercentage nominaalPercentage converteert naar een jaarlijks effectief percentage, waarbij CpY het aantal samengestelde periodes per jaar is. nominaalPercentage moet een reëel getal zijn, en CpY moet een reëel getal > 0 zijn. Opmerking: zie ook nom(), hier. |
|
|
Catalogus > |
|
|
eigVc(vierkanteMatrix)Þmatrix Geeft een matrix met de eigenvectoren voor een reële of complexe vierkanteMatrix, waarbij elke kolom in het resultaat overeenkomt met een eigenwaarde. Merk op dat een eigenvector niet uniek is; hij kan geschaald worden door een willekeurige constante factor. De eigenvectoren worden genormaliseerd, wat betekent: als V = [x1, x2, …, xn], dan: x12 + x22 + … + xn2 = 1 vierkanteMatrix wordt eerst gebalanceerd met gelijkheidstransformaties tot de rij- en kolomnormen zo dicht mogelijk bij dezelfde waarde liggen. vierkanteMatrix wordt vervolgens gereduceerd tot de upper-Hessenberg-vorm en de eigenvectoren worden berekend via een Schur-factorisatie. |
In rechthoekige complexe opmaak:
Om het hele resultaat te zien drukt u op 5 en gebruikt u vervolgens 7 en 8 om de cursor te verplaatsen. |
|
Catalogus > |
|
|
eigVl(vierkanteMatrix)Þlijst Geeft een lijst van de eigenwaarden van een reële of complexe vierkanteMatrix. vierkanteMatrix wordt eerst gebalanceerd met gelijkheidstransformaties tot de rij- en kolomnormen zo dicht mogelijk bij dezelfde waarde liggen. vierkanteMatrix wordt vervolgens gereduceerd tot de upper-Hessenberg-vorm en de eigenwaarden worden berekend uit de upper-Hessenberg-matrix. |
In de rechthoekige complexe opmaak-modus:
Om het hele resultaat te zien drukt u op 5 en gebruikt u vervolgens 7 en 8 om de cursor te verplaatsen. |
|
Zie If, hier. |
|
|
|
|
|
Catalogus > |
|
|
Als BooleaanseUitdr1 Then Opmerking bij het invoeren van het voorbeeld: Instructies over het invoeren van programma's met meerdere regels en functiedefinities vindt u in het hoofdstuk Rekenmachine van de handleiding van uw product. |
|
|
Zie For, hier. |
|
|
|
|
|
Zie Func, hier. |
|
|
|
|
|
Zie If, hier. |
|
|
|
|
|
Zie Loop, hier. |
|
|
|
|
|
Zie Prgm, hier. |
|
|
|
|
|
Zie Try, hier. |
|
|
|
|
|
Zie While, hier. |
|
|
|
|
|
Catalogus > |
|
|
Gebruikt de Euler-methode om het stelsel
op te lossen met afhVar(Var0)=afhVar0 op het interval [Var0,VarMax]. Geeft een matrix waarvan de eerste rij de Var-uitvoerwaarden definieert, en de tweede rij de waarde van de eerste oplossingscomponent bij de overeenkomstige Var-waarden definieert, enzovoort. Uitdr is de rechterzijde die de gewone differentiaalvergelijking (GDV) definieert. StelselUitdr is het stelsel van de rechterleden die het stelsel van GDV's definieren (komt overeen met de volgorde van afhankelijke variabelen in LijstVanAfhVars). StelselUitdr is een lijst van de rechterleden die het stelsel van GDV's definieren (komt overeen met de volgorde van afhankelijke variabelen in LijstVanAfhVars). Var is de onafhankelijke variable. LijstVanAfhVars is een lijst van afhankelijke variabelen. {Var0, VarMax} is een lijst met twee elementen die de functie vertelt om van Var0 tot VarMax te integreren. LijstVanAfhVars0 is een lijst met beginwaarden voor afhankelijke variabelen. VarStap is een getal dat niet nul is, zodanig dat eulerStap is een positief geheel getal (standaardwaarde is 1) dat het aantal eulerstappen tussen uitvoerwaarden definieert. De feitelijke stapgrootte die gebruikt wordt door de eulermethode is VarStapàeulerStap. |
Differentiaalvergelijking: y'=0,001*y*(100-y) en y(0)=10
Om het volledige resultaat te zien drukt u op £ en gebruikt u vervolgens ¡ en ¢ om de cursor te verplaatsen.
Stelsel vergelijkingen:
met y1(0)=2 en y2(0)=5
|
|
Hub Menu |
|
|
eval() is alleen geldig in het TI-Innovator™ Hub argument van de programmeeropdrachten Get, GetStr, en Send. De software werkt de uitdrukking Expr uit en vervangt eval() door het resultaat daarvan, in de vorm van een tekenreeks (string). Het argument Expr moet vereenvoudigd kunnen worden tot een reëel getal. |
Stel het blauwe deel van de RGB LED in op halve intensiteit.
Zet het blauwe element terug op OFF (UIT).
Het argument van eval() moet vereenvoudigd kunnen worden tot een reëel getal.
Programma om het rode element in te faden
Voer het programma uit.
|
|
Hoewel eval() het resultaat niet weergeeft, kunt u de Hub opdracht string die het resultaat is na het uitvoeren van de opdracht bekijken door een van de volgende speciale variabelen te onderzoeken. iostr.SendAns Opmerking: Zie ook Get (hier), GetStr (hier), en Send (hier). |
|
|
Catalogus > |
|
|
Exit Sluit het huidige For, While of Loop-blok af. Exit is niet toegestaan buiten de drie lusstructuren (For, While of Loop). Opmerking bij het invoeren van het voorbeeld: Instructies over het invoeren van programma's met meerdere regels en functiedefinities vindt u in het hoofdstuk Rekenmachine van de handleiding van uw product. |
Functielijst:
|
|
u-toets |
|
|
exp(Waarde1)Þwaarde Geeft e tot de macht Waarde1. Opmerking: zie ook e exponent-template, hier. U kunt een complex getal in rei q polaire vorm invoeren. Gebruik deze vorm echter alleen in de hoekmodus Radialen; hij veroorzaakt een domeinfout in de hoekmodi Graden en Decimale graden. |
|
|
exp(Lijst1)Þlijst Geeft e tot de macht van elk element in Lijst1. |
|
|
exp(vierkanteMatrix1)ÞvierkanteMatrix Geeft de 'e tot de macht van vierkanteMatrix1'. Dit is niet hetzelfde als het berekenen van e tot de macht van elk element. Zie voor informatie over de berekeningsmethode cos(). vierkanteMatrix1 moet diagonaliseerbaar zijn. Het resultaat bevat altijd getallen met een drijvende komma. |
|
|
Catalogus > |
|
|
expr(String)Þuitdrukking Geeft de tekenreeks in String als een uitdrukking en voert deze onmiddellijk uit. |
|
|
Catalogus > |
|
|
ExpReg X, Y [, [Freq][, Categorie, Opnemen]] Berekent de exponentiële regressiey = a·(b)xop de lijsten X en Y met frequentie Freq. Een samenvatting van de resultaten wordt opgeslagen in de variabele stat.resultaten (hier). Alle lijsten moeten gelijke afmetingen hebben, behalve Opnemen. X en Y zijn lijsten met onafhankelijke en afhankelijke variabelen. Freq is een optionele lijst met frequentiewaarden. Elk element in Freq specificeert de frequentie waarmee elk overeenkomstig X- en Y-gegeven voorkomt. De standaardwaarde is 1. Alle elementen moeten gehele getallen | 0 zijn. Categorie is een lijst met Opnemen is een lijst met één of meer van de categoriecodes. Alleen de gegevens waarvan de categoriecode is opgenomen in deze lijst worden opgenomen in de berekening. Zie voor informatie over het effect van lege elementen in een lijst “Lege elementen” (hier). |
|
|
Uitvoervariabele |
Beschrijving |
|
stat.RegEqn |
Regressievergelijking: a·(b)x |
|
stat.a, stat.b |
Regressiecoëfficiënten |
|
stat.r2 |
Coëfficiënt van lineaire verband voor getransformeerde gegevens |
|
stat.r |
Correlatiecoëfficiënt voor getransformeerde gegevens (x, ln(y)) |
|
stat.Resid |
Residuen die geassocieerd zijn met het exponentiële model |
|
stat.ResidTrans |
Residuen die geassocieerd zijn met de lineaire regressie van getransformeerde gegevens |
|
stat.XReg |
Lijst van de gegevens in de gemodificeerde XLijst die feitelijk gebruikt worden in de regressie op basis van beperkingen van Freq, Categorielijst en Categorieën opnemen |
|
stat.YReg |
Lijst van gegevens in de gemodificeerde YLijst die feitelijk gebruikt worden in de regressie op basis van beperkingen van Freq, Categorielijst en Categorieën opnemen |
|
stat.FreqReg |
Lijst van frequenties die corresponderen met stat.XReg en stat.YReg |