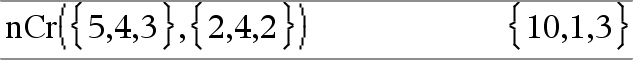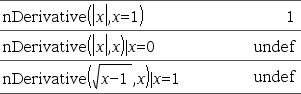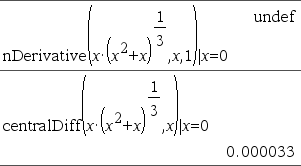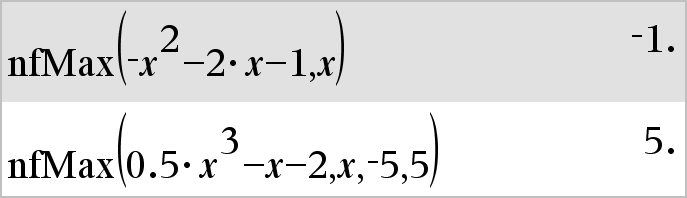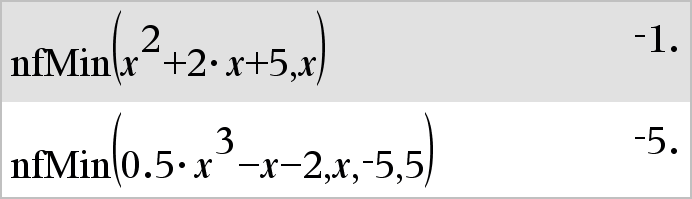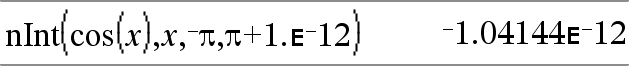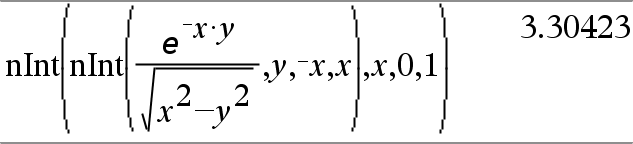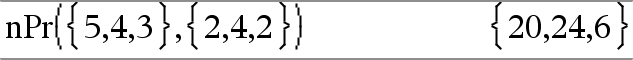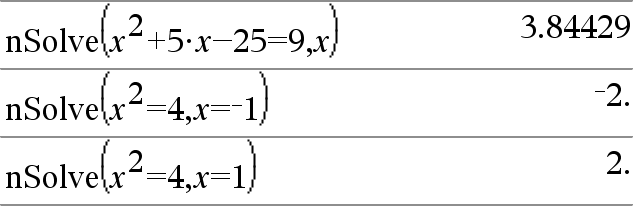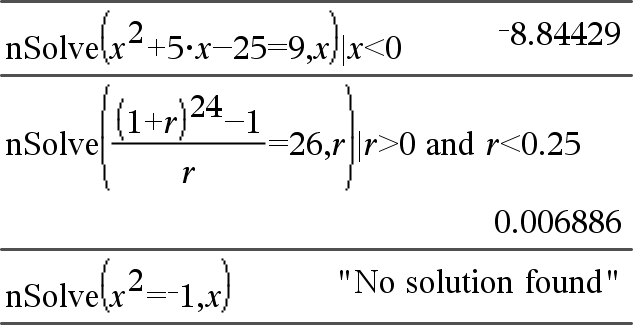|
/= toetsen |
|
|
BooleaanseUitdr1 BooleaanseLijst1 BooleaanseMatrix1
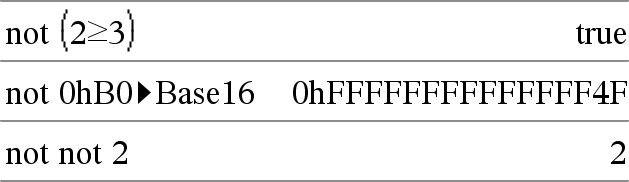
Geeft de ontkenning (negatie) van een logische Bij lijsten en matrices vergelijkt dit commando element voor element. |
|
|
Geheel getal1 Vergelijkt twee reële gehele getallen bit voor bit met behulp van een U kunt de gehele getallen invoeren in elk talstelsel. Voor een binaire of hexadecimale invoer moet u respectievelijk het voorvoegsel 0b of 0h gebruiken. Zonder voorvoegsel worden gehele getallen behandeld als decimaal (grondtal 10). |
|
|
Catalogus > |
|
|
nCr(Waarde1, Waarde2)Þuitdrukking Voor geheel getal Waarde1 en Waarde2 met Waarde1 | Waarde2 | 0, is nCr() het aantal combinaties van Waarde1 dingen die met Waarde2 keer tegelijk genomen zijn. (Dit is ook bekend als een binomiale coëfficiënt.) nCr(Waarde, 0)Þ1 nCr(Waarde, negGeheel getal)Þ0 nCr(Waarde, posGeheel getal)Þ Waarde·(WaardeN1)... (WaardeNposGeheel getal+1)/ posGeheel getal!
|
|
|
nCr(Lijst1, Lijst2)Þlijst Geeft een lijst met combinaties op basis van de overeenkomstige elementparen in de twee lijsten. De argumenten moeten lijsten van dezelfde afmeting zijn. |
|
|
nCr(Matrix1, Matrix2)Þmatrix Geeft een matrix met combinaties op basis van de overeenkomstige elementparen in de twee matrices. De argumenten moeten matrices van dezelfde afmeting zijn. |
|
|
Catalogus > |
|
|
Geeft de numerieke afgeleide die berekend is met automatische differentiatiemethodes. Wanneer Waarde gespecificeerd is, wordt elke eerdere variabeletoekenning of elke huidige “|”-substitutie voor de variabele onderdrukt. Als de variabele Var geen numerieke waarde bevat, moet u Waarde opgeven. Orde van de afgeleide moet 1 of 2 zijn. |
|
|
Zie het voorbeeld rechts. De eerste afgeleide van x·(x^2+x)^(1/3) voor x=0 is gelijk aan 0. Omdat de eerste afgeleide van de subuitdrukking (x^2+x)^(1/3) echter onbepaald is voor x=0, en deze waarde gebruikt wordt om de afgeleide van de gehele uitdrukking te berekenen, geeft nDerivative() de uitkomst als onbepaald en toont een waarschuwingsbericht. Als u deze beperking tegenkomt, verifieer de oplossing dan grafisch. U kunt ook proberen centralDiff() te gebruiken. |
|
|
Catalogus > |
|
|
newList(aantalElementen)Þlijst Geeft een lijst met de afmeting aantalElementen. Elk element is nul. |
|
|
Catalogus > |
|
|
newMat(aantalRijen, aantalKolommen)Þmatrix Geeft een matrix met nullen met de afmeting aantalRijen bij aantalKolommen. |
|
|
Catalogus > |
|
|
nfMax(Uitdr, Var)Þwaarde nfMax(Uitdr, Var, ondergrens)Þwaarde nfMax(Uitdr, Var, ondergrens, bovengrens)Þwaarde nfMax(Uitdr, Var) | ondergrens{Var{bovengrensÞwaarde Geeft een mogelijke numerieke waarde van variabele Var waarvoor het lokale maximum van Uitdr optreedt. Als u ondergrens en bovengrens opgeeft, zoekt de functie binnen het gesloten interval [ondergrens,bovengrens] naar het lokale maximum. |
|
|
Catalogus > |
|
|
nfMin(Uitdr, Var)Þwaarde nfMin(Uitdr, Var, ondergrens)Þwaarde nfMin(Uitdr, Var, ondergrens, bovengrens)Þwaarde nfMin(Uitdr, Var) | ondergrens{Var{bovengrensÞwaarde Geeft een mogelijke numerieke waarde van variabele Var waarvoor het lokale minimum van Uitdr optreedt. Als u ondergrens en bovengrens opgeeft, zoekt de functie binnen het gesloten interval [ondergrens,bovengrens] naar het lokale minimum. |
|
|
Catalogus > |
|
|
nInt(Uitdr1, Var, Onder, Boven)Þuitdrukking Als de integrand Uitdr1 geen andere variabele dan Var bevat, en als Onder en Boven constanten, positief ˆ of negatief ˆ zijn, dan geeft nInt() een benadering van ‰(Uitdr1, Var, Onder, Boven). Deze benadering is een gewogen gemiddelde van enkele steekproefwaarden van de integrand in het interval Onder<Var<Boven. |
|
|
Het doel is zes significante cijfers. Het adaptieve algoritme eindigt wanneer het waarschijnlijk lijkt dat het doel is bereikt, of wanneer het onwaarschijnlijk lijkt dat extra steekproeven een lonende verbetering zullen opleveren. Er wordt een waarschuwing weergegeven (“Twijfelachtige nauwkeurigheid”) wanneer het erop lijkt dat het doel niet is bereikt. |
|
|
Nest nInt() om meervoudige numerieke integratie uit te voeren. Integratiegrenzen kunnen afhangen van integratievariabelen erbuiten. |
|
|
Catalogus > |
|
|
nom(effectiefPercentage,CpY)Þwaarde Financiële functie die het jaarlijkse effectieve rentepercentage effectiefPercentage naar een nominaal percentage converteert, waarbij CpY het aantal rentetermijnen per jaar is. effectiefPercentage moet een reëel getal zijn en CpY moet een reëel getal > 0 zijn. Opmerking: zie ook eff(), hier. |
|
|
/= toetsen |
|
|
BooleaanseUitdr1
BooleaanseLijst1
BooleaanseMatrix1
Geeft de ontkenning (negatie) van een logische Bij lijsten en matrices vergelijkt dit commando element voor element. |
|
|
Geheel getal1
Vergelijkt twee reële gehele getallen bit voor bit met behulp van een U kunt de gehele getallen invoeren in elk talstelsel. Voor een binaire of hexadecimale invoer moet u respectievelijk het voorvoegsel 0b of 0h gebruiken. Zonder voorvoegsel worden gehele getallen behandeld als decimaal (grondtal 10). |
|
|
Catalogus > |
|
|
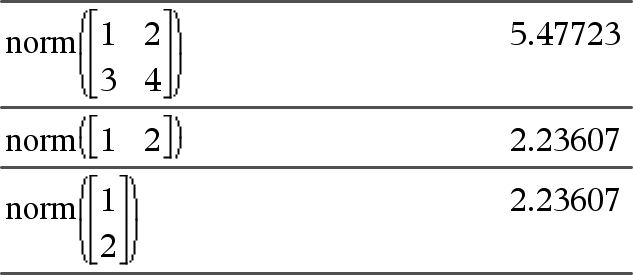
norm(Matrix)Þuitdrukking norm(Vector)Þuitdrukking Geeft de Frobenius-norm. |
|
|
Catalogus > |
|
|
normCdf(ondergrens,bovengrens[,m[,s]])Þgetal als ondergrens en bovengrens getallen zijn, lijst als ondergrens en bovengrens lijsten zijn Berekent de normale verdelingskans tussen ondergrens en bovengrens voor de gespecificeerde m (standaard=0) en s (standaard=1).
|
|
|
Catalogus > |
|
|
normPdf(XWaarde[,m[,s]])Þgetal als XWaarde een getal is, lijst als XWaarde een lijst is Berekent de kansdichtheidsfunctie voor de normale verdeling bij een gespecificeerde XWaarde voor de gespecificeerde m en s. |
|
|
Catalogus > |
|
|
not BooleaanseUitdrÞBooleaanse uitdrukking Geeft waar, onwaar of een vereenvoudigde vorm van het argument. |
|
|
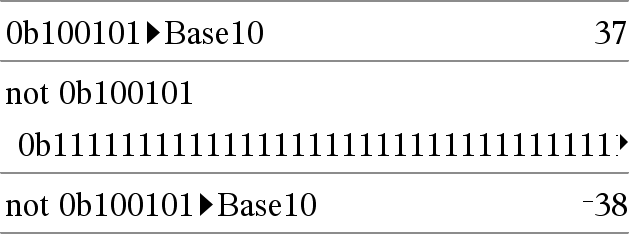
not Geheel getal1Þgeheel getal Geeft het één-complement van een reëel geheel getal. Intern wordt Geheel getal1 geconverteerd naar een 64-bits binair getal met een plus- of min-teken. De waarde van elke bit wordt omgewisseld (0 wordt 1 en andersom) voor het één-complement. Resultaten worden weergegeven volgens de grondtal-modus. U kunt het gehele getal in elk grondtal invoeren. Voor een binaire of hexadecimale invoer moet u respectievelijk het prefix 0b of 0h gebruiken. Zonder prefix wordt het gehele getal behandeld als decimaal (grondtal 10). Als u een decimaal geheel getal invoert dat te groot is voor een 64-bits binaire vorm met een teken (positief of negatief), dan wordt er een symmetrische modulo-bewerking gebruikt om de waarde binnen het betreffende bereik te brengen. Zie voor meer informatie 4Base2, hier. |
In de Hex-grondtalmodus: Belangrijk: nul, niet de letter O.
In de Bin-grondtalmodus:
Om het hele resultaat te zien drukt u op 5 en gebruikt u vervolgens 7 en 8 om de cursor te verplaatsen. Opmerking: een binaire invoer kan maximaal 64 cijfers hebben (het prefix 0b niet meegeteld). Een hexadecimale invoer kan maximaal 16 cijfers hebben. |
|
Catalogus > |
|
|
nPr(Waarde1, Waarde2)Þuitdrukking Voor geheel getal Waarde1 en Waarde2 met Waarde1 | Waarde2 | 0, is nPr() het aantal permutaties van Waarde1 dingen die met Waarde2 tegelijk genomen zijn. nPr(Waarde, 0)Þ1 nPr(Waarde, negGeheel getal)Þ 1/((Waarde+1)·(Waarde+2)... (WaardeNnegGeheel getal)) nPr(Waarde, posGeheel getal)Þ Waarde·(WaardeN1)... (WaardeNposGeheel getal+1)
|
|
|
nPr(Lijst1, Lijst2)Þlijst Geeft een lijst met permutaties op basis van de overeenkomstige elementparen in de twee lijsten. De argumenten moeten lijsten van dezelfde afmeting zijn. |
|
|
nPr(Matrix1, Matrix2)Þmatrix Geeft een matrix met permutaties op basis van de overeenkomstige elementparen in de twee matrices. De argumenten moeten matrices van dezelfde afmeting zijn. |
|
|
Catalogus > |
|
|
npv(RentePercentage,CFO,CFLijst[,CFFreq]) Financiële functie die de netto contante waarde berekent; de som van de contante waarden voor de kasinstromen en -uitstromen. Een positief resultaat voor npv duidt op een winstgevende investering. RentePercentage is de rente waarmee de cashflows verdisconteerd moeten worden (de kosten van het geld) over één periode. CF0 is de begin-cashflow op tijdstip 0; dit moet een reëel getal zijn. CFLijst is een lijst met cashflow-bedragen na de begin-cashflow CF0. CFFreq is een lijst waarin elk element de frequentie waarmee een gegroepeerde (opeenvolgend) cashflow-bedrag voorkomt specificeert; dit is het overeenkomstige element vanCFLijst. De standaardwaarde is 1; als u waarden invoert, dan moeten dit positieve gehele getallen < 10.000 zijn. |
|
|
Catalogus > |
|
|
nSolve(Vergelijking,Var[=Gok])Þgetal of fout_string nSolve(Vergelijking,Var[=Gok],ondergrens)Þgetal of fout_string nSolve(Vergelijking,Var[=Gok],ondergrens,bovengrens) Þgetal of fout_string nSolve(Vergelijking,Var[=Gok]) | ondergrens{Var{bovengrensÞgetal of fout_string Zoekt iteratief naar één benaderende numerieke oplossing van Vergelijking, voor de ene variabele ervan. Specificeer de variabele als: variabele – of – variabele = reëel getal Bijvoorbeeld: x is geldig en x=3 ook. |
Opmerking: als er meerdere oplossingen zijn, dan kunt u een gok gebruiken om een bepaalde oplossing te helpen vinden. |
|
nSolve() probeert één punt te bepalen waarop het residu nul is, of twee relatief dicht bij elkaar liggende punten waarop het residu tegenovergestelde tekens heeft, en de grootte van het residu niet overdreven is. Als dit niet bereikt kan worden met behulp van een bescheiden aantal steekproefpunten, dan wordt de string “geen oplossing gevonden” gegeven. |
|