Vous pouvez exécuter des calculs statistiques afin d’analyser les données. L’exemple suivant correspond à un modèle de régression linéaire de type y = mx + b s’appliquant à deux listes dans les colonnes A et B.

1.

Dans le menu Statistiques, sélectionnez Calculs statistiques>, puis Ajustement linéaire (mx + b) pour choisir le modèle de régression

La boîte de dialogue Régression linéaire (mx + b) s’ouvre.

2.

Tapez a[] en tant que colonne de la Liste X.

3.

Tapez b[] en tant que colonne de la Liste Y.

4.

Pour enregistrer l’équation de régression dans une variable spécifiée, remplacez Enregistrer RegEqn dans par le nom de la variable.

5.

Tapez c[] en tant que colonne du 1er résultat.

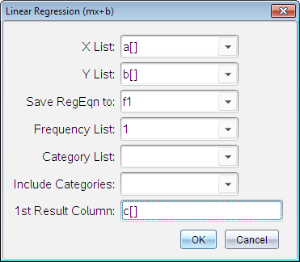
6.

Cliquez sur OK.

L’application Tableur & listes insère deux colonnes : la première affichant les noms résultants et la seconde les valeurs correspondantes

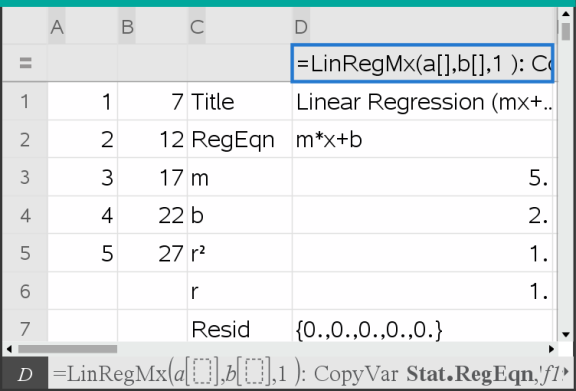
Remarque : les résultats sont liés aux données sources. Par exemple, si vous modifiez une valeur de la colonne A, l’équation de régression est automatiquement actualisée.

 

L’application Tableur & listes stocke automatiquement les résultats sous un nom de groupe de variables, sous la forme stat.nnn, où nnn est le nom du résultat (par exemple, stat.RegEqn et stat.Resid). L’utilisation de noms standard pour les variables simplifie l’identification et l’utilisation ultérieures des variables statistiques. Vous pouvez modifier la formule dans la cellule de formule afin d’utiliser un nom de groupe de variables personnalisé plutôt que le nom standard.

Vous pouvez ainsi utiliser la formule suivante pour stocker les résultats dans le groupe de variables MystatsB.

=LinRegMx(a[],b[],1 ): CopyVar Stat., MystatsB.

Par la suite, si vous voulez afficher les résultats, il vous suffit de taper l’expression suivante dans l’application Calculs ou dans une autre colonne de l’application Tableur & listes :

MystatsB.results

 

Le menu Calculs statistiques permet de sélectionner les calculs décrits ci-dessous. Pour plus d’informations, voir le manuel d’utilisation de TI-Nspire  ™.

OneVar, statistiques à une variable

Analyse les données avec une variable mesurée. Vous pouvez spécifier une liste de fréquences optionnelle. Les données statistiques obtenues à l’aide de cette technique analytique sont :

•

Moyenne de l’échantillon, x

•

Somme des données, Gx

•

Somme des carrés des données, Gx2

•

Écart type d’échantillon, sx

•

Écart type de population, sx

•

Taille de l’échantillon, n

•

X-min

•

Premier quartile, Q1

•

Médiane

•

Troisième quartile, Q3

•

X-max

•

Somme des écarts quadratiques, SSx = G(x Nx)2

Statistiques à deux variables (TwoVar)

Analyse des données appariées. Liste 1 est la variable indépendante. Liste 2 est la variable dépendante. Vous pouvez spécifier une liste de fréquences optionnelle. Les données statistiques obtenues à l’aide de cette technique analytique sont :

Pour chaque liste :

•

Moyenne de l’échantillon, x ou y

•

Somme des données, Gx ou Gy

•

Somme des carrés des données, Gx2 ou Gy2

•

Écart type d’échantillon, sx = sn-1x ou sy = sn-1y

•

Écart type de population, sx = snx ou sy = sny

•

X-min ou Y-min

•

Premier quartile, Q1X ou Q1Y

•

Médiane

•

Troisième quartile, Q3X ou Q3Y

•

X-max ou Y-max

•

Sommes des écarts quadratiques, SSx = G(x Nx)2 ou SSy = G(y Ny)2

Données supplémentaires :

•

Taille de l’échantillon pour chaque ensemble de données, n

•

Gxy

•

Coefficient de corrélation, R.

Régression linéaire (mx+b) (LinRegMx)

Ajuste l’équation modèle y = mx + b aux données, en utilisant la méthode des moindres carrés. Elle affiche les valeurs de m (pente) et b (ordonnée de l’intersectionavec l’axe des y-).

Régression linéaire (a+bx) (LinRegBx)

Ajuste l’équation modèle y = a + bx aux données, en utilisant la méthode des moindres carrés. Elle affiche les valeurs de a (ordonnée de l’intersection avec l’axe des y-), b (pente), r2 et r.

Régression médiane-médiane (MedMed)

Ajuste aux données l’équation modèle y = mx + b en utilisant la technique de la droite médiane-médiane (ligne de résistance) et en calculant les points médians x1, y1, x2, y2, x3 et y3. La -droite médiane-médiane affiche les valeurs de m (pente) et b (ordonnée de l’intersection avec l’axe des y-).

Régression de degré 2 (QuadReg)

Ajuste aux données le polynôme de second degré y = ax2 + bx + c. Elle affiche les valeurs de a, b, c et R2. Pour trois points de données, l’équation est celle du polynôme d’interpolation associé à ces trois points ; pour quatre ou plus, il s’agit d’une régression polynomiale. Un minimum de trois points de données est nécessaire.

Régression de degré 3 (CubicReg)

Ajuste le polynôme du troisième degré y = ax3 + bx2 + cx + d aux données. Elle affiche les valeurs de a, b, c, d et R2. Pour quatre points de données, l’équation est celle du polynôme d’interpolation associé à ces quatre points ; pour cinq ou plus, il s’agit d’une régression polynomiale. Un minimum de quatre points est nécessaire.

Régression de degré 4 (QuartReg)

Ajuste le polynôme du quatrième degré y = ax4 + bx3 + cx2 + dx + e aux données. Elle affiche les valeurs de a, b, c, d, e et R2. Pour cinq points de données, l’équation est celle du polynôme d’interpolation associé à ces cinq points ; pour six ou plus, il s’agit d’une régression polynomiale. Un minimum de cinq points est nécessaire.

Régression puissance (PowerReg)

Ajuste les données en fonction de l’équation de type y = axb en utilisant la méthode des moindres carrés appliquée aux valeurs transformées ln(x) et ln(y). Elle affiche les valeurs de a, b, r2 et r.

Régression exponentielle (ExpReg)

Ajuste l’équation modèle y = abx aux données en utilisant la méthode des moindres carrés appliquée aux valeurs transformées x et ln(y). Elle affiche les valeurs de a, b, r2 et r.

Régression logarithmique (LogReg)

Ajuste les données en fonction de l’équation de type y = a + b ln(x) en utilisant la méthode des moindres carrés appliquée aux valeurs transformées ln(x) et y. Elle affiche les valeurs de a, b, r2 et r.

Régression sinusoïdale (SinReg)

Ajuste l’équation modèle y = a sin(bx + c) + d aux données en utilisant une méthode itérative des moindres carrés. Elle affiche les valeurs de a, b, c et d. Un minimum de quatre points de données est nécessaire. Au moins deux points de données par cycle sont nécessaires afin d’éviter des valeurs de fréquence approximatives.

Remarque : Le résultat obtenu avec SinReg est toujours exprimé en radians, indépendamment du mode Radian/Degré paramétré.

Régression logistique (d=0) (Logistic)

La régression logistique ajuste l’équation modèle y = c/(1 + a*e-Lbx) aux données en utilisant une méthode itérative des moindres carrés. Elle affiche les valeurs de a, b et c.

Régression logistique (dƒ0) (LogisticD)

Ajuste l’équation modèle y = c(1 + a*e(-bx)) + d aux données en utilisant une méthode itérative des moindres carrés. Elle affiche les valeurs de a, b, c et d.

Régression linéaire multiple (MultReg)

Calcule la régression linéaire multiple de la liste Y sur les listes X1, X2, …, X10