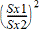Tests statistiques pris en charge
Les tests d’hypothèse suivants sont accessibles depuis l’application Tableur & listes. Pour plus d’informations sur ces fonctions, consultez le Manuel de l’utilisateur TI-Nspire™.
Certains assistants Tests statistiques affichent une case à cocher Dessiner. Cette case à cocher n’est pas sélectionnée par défaut. Cocher cette case a pour effet d’ouvrir un espace de travail Données & statistiques sur la page en cours et d’y représenter les résultats.
z test (zTest)
Teste une hypothèse pour une moyenne inconnue de population m quand l’écart-type de population s est connu. Il teste l’hypothèse nulle H0 : m=m0 contre l’une des alternatives ci-dessous.
| • | Ha : mƒm0 |
| • | Ha : m<m0 |
| • | Ha : m>m0 |
Ce test est utilisé pour les populations de grande taille normalement réparties. L’écart type doit être connu.
Ce test permet de déterminer si la différence entre une moyenne d’échantillon et une moyenne de population est statistiquement significative lorsque l’on connaît le véritable écart type d’une population.
t test (tTest)
Teste une hypothèse pour la moyenne inconnue d’une population m quand l’écart-type de la population s est inconnu. Il teste l’hypothèse nulle H0 : m=m0 contre l’une des alternatives ci-dessous.
| • | Ha: mƒm0 |
| • | Ha: m<m0 |
| • | Ha : m>m0 |
Ce test est similaire au z-test mais est utilisé lorsque la population est de petite taille et est normalement répartie. Il est utilisé plus souvent que le z-test car il est plus courant de rencontrer dans les statistiques des populations de petite taille que des populations de grande taille.
Ce test est utile pour déterminer si deux populations normalement réparties présentent des moyennes identiques ou lorsque vous devez déterminer si une moyenne d’échantillon diverge significativement d’une moyenne de population lorsque l’écart type de la population est inconnu.
z-Test sur 2 échantillons (zTest_2Samp)
z-Test sur 2 échantillons teste l’égalité des moyennes de deux populations (m1 et m2) sur la base d’échantillons indépendants lorsque les deux écarts types des deux populations (s1 et s2) sont connus. L’hypothèse nulle H0 : m1 = m2 est testée contre l’une des hypothèses ci-dessous.
| • | Ha : m1ƒm2 |
| • | Ha : m1<m2 |
| • | Ha: m1>m2 |
t-Test sur 2 échantillons (tTest_2Samp)
t-Test sur 2 échantillons teste l’égalité des moyennes de deux populations (m1 et m2) sur la base d’échantillons indépendants quand aucun écart type des populations (s1 ou s2) n’est connu. L’hypothèse nulle H0: m1=m2 est testée contre l’une des hypothèses ci-dessous.
| • | Ha: m1ƒm2 |
| • | Ha: m1<m2 |
| • | Ha: m1>m2 |
z-Test pour 1 proportion (zTest_1Prop)
Z-Test pour 1 proportion calcule un test pour une proportion inconnue de succès (prop). Le test prend comme entrée le nombre de succès dans l’échantillon x et le nombre d’observations dans l’échantillon n. 1-Prop z Test teste l’hypothèse nulle H0 : prop = p0 contre l’une des alternatives ci-dessous.
| • | Ha : propƒp0 |
| • | Ha : prop<p0 |
| • | Ha : prop>p0 |
Ce test permet de déterminer si la fréquence de succès constatée dans un échantillon est significativement différente de la probabilité de succès dans la population ou si cela est dû à une erreur d’échantillonnage, à un écart ou à d’autres facteurs.
z-Test pour 2 proportions (zTest_2Prop)
z-Test pour 2 proportions compare la proportion des succès (p1 et p2) issus de deux populations. Le test prend comme entrée le nombre de succès dans chaque échantillon (x1 et x2) et le nombre d’observations dans chaque échantillon (n1 et n2). 2-Prop z Test teste l’hypothèse nulle H0 : p1 = p2 (en utilisant la proportion de l’échantillon groupé Ç) contre une des alternatives ci-dessous.
| • | Ha : p1ƒp2 |
| • | Ha : p1<p2 |
| • | Ha : p1>p2 |
Ce test permet de déterminer si la probabilité de succès constatée dans deux échantillons est identique.
ADEc2 (c2GOF)
Effectue un test pour s’assurer que les données des échantillons sont issues d’une population conforme à la loi spécifiée. Par exemple, ADE c2 peut confirmer que les données de l’échantillon proviennent d’une répartition normale.
c2 (c22way)
Le test c2 (test chi deux) calcule un test chi deux pour le lien sur un tableau à deux entrées dans la matrice Observée spécifiée. L’hypothèse nulle H0 pour un tableau à double entrée est : aucune association n’existe entre les variables de ligne et de colonne. L’hypothèse alternative est : les variables sont liées.
FTest à 2 échantillons (FTest_2Samp)
Ce test calcule un F-test pour comparer les écarts types de deux populations (s1 et s2). Les moyennes des populations et les écarts types sont tous inconnus. F Test à-2échantillons , qui exploite le rapport des variances de l’échantillon Sx12/Sx22, teste l’hypothèse nulle H0 :s1 = s2 contre une des alternatives ci-dessous.
| • | Ha : s1ƒs2 |
| • | Ha : s1<s2 |
| • | Ha : s1>s2 |
Vous trouverez ci-dessous une définition du - FTest sur deux échantillons.
|
Sx1, Sx2 |
= |
Exemples d’écart-type avec n1N1 et n2N1 degrés de liberté df, respectivement. |
|
|
|
F-statistique = |
|
df(x, n1N1, n2N1) |
= |
Fpdf( ) avec degrés de liberté df, n1N1, et n2N1 |
|
p |
= |
valeur p rapportée |
F- Test à 2 échantillons pour l’hypothèse alternative s1 > s2.
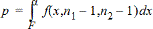
F- Test à 2 échantillons pour l’hypothèse alternative s1 < s2.
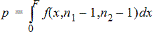
F Test à 2-échantillons pour l’hypothèse alternative s1ƒs2. Les limites doivent satisfaire aux conditions suivantes :
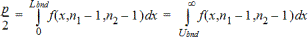
où : [Lbnd,Ubnd]=limite inférieure et limite supérieure
La statistique F- sert de borne produisant la plus petite intégrale. L’autre borne est sélectionnée pour obtenir la relation d’égalité de l’intégrale précédente.
t Test de régression linéaire (LinRegtTest)
LinRegTTest (t-test avec régression linéaire) calcule la régression linéaire des données et effectue un test t sur la valeur de la pente b et sur le coefficient de corrélation r pour l’équation y = a + bx. Il teste l’hypothèse nulle H0 : b = 0 (en équivalence, r = 0) contre l’une des alternatives ci-dessous.
| • | Ha : bƒ0 et rƒ0 |
| • | Ha : b<0 et r<0 |
| • | Ha : b>0 et r>0 |
Tests de régressions multiples (MultRegTest)
Calcule une régression linéaire sur les données et effectue un test f statistique de linéarité.
Pour plus d’informations, voir le manuel d’utilisation de l’unité TI-Nspire™.
ANOVA (ANOVA)
Le test effectue une analyse de variance unidimensionnelle pour comparer les moyennes de deux à vingt populations. Le test ANOVA de comparaison de moyennes comprend l’analyse de la variation dans les données de l’échantillon. L’hypothèse nulle H0 : m1 = m2 = ...=mk est testée par rapport à l’alternative Ha : tous les m1...mk ne sont pas égaux.
Le test ANOVA permet de déterminer s’il y a une différence significative entre les groupes par rapport à la différence constatée au sein de chaque groupe.
Il permet de déterminer si la variation des données entre les échantillons montre une influence statistiquement significative provenant d’un facteur autre que la variation constatée au sein des ensembles de données eux-mêmes. Prenons l’exemple d’une société d’expédition voulant acheter des cartons. Elle hésite entre trois fabricants. Elle examine les échantillons de carton envoyés par les trois fabricants. L’analyse ANOVA peut l’aider à déterminer si les différences entre chaque groupe d’échantillon sont significatives par rapport aux différences constatées au sein de chaque groupe d’échantillon.
ANOVA à deux facteurs (ANOVA2way)
Le test effectue une analyse de variance bidimensionnelle pour comparer les moyennes de deux à vingt populations. Un récapitulatif des résultats est stocké dans la variable stat.results.
L’analyse de variance ANOVA à deux facteurs étudie les effets de deux variables indépendantes et permet de déterminer si elles interagissent par rapport à la variable dépendante. En d’autres termes, si les deux variables indépendantes interagissent, leur effet combiné peut être supérieur ou inférieur à l’impact de l’une ou l’autre variable indépendante.
Ce test permettant d’évaluer les différences, est similaire à l’analyse ANOVA, mais prend en compte une autre influence potentielle. Pour reprendre l’exemple des cartons présenté plus haut, l’analyse ANOVA à deux facteurs pourra étudier l’influence du matériau de composition des cartons sur les différences constatées.
Sélection d’une hypothèse alternative (ƒ < >)
La plupart des éditeurs de statistiques inférentielles pour les tests d’hypothèse vous invitent à sélectionner l’une des trois hypothèses alternatives.
| • | La première est une hypothèse alternative de type ƒ, comme mƒm0 pour le z Test. |
| • | La deuxième est une hypothèse alternative de type <, comme m1<m2 pour le t Test sur 2-échantillons . |
| • | La troisième est une hypothèse alternative de type >, comme p1>p2 pour le z Test pour 2-proportions . |
Pour sélectionner une hypothèse alternative, déplacer le curseur sur l’alternative appropriée et appuyez sur Entrée.
Sélection de l’option grouper
L’option grouper (t Test sur 2-échantillons et t Intervalle sur 2-échantillons seulement) indique si les variances doivent être regroupées pour effectuer le calcul.
| • | Sélectionnez Non (No) si vous ne souhaitez pas grouper les variances. Les variances de population peuvent être inégales. |
| • | Sélectionnez Oui (Yes) si vous souhaitez grouper les variances. Les variances de population sont réputées être égales. |
Pour sélectionner l’option grouper, cliquez sur Oui (Yes) dans le champ déroulant.